Раздел 8.
Конические зубчатые передачи.
Зубчатые передачи с зацеплением Новикова.
Планетарные зубчатые передачи. Волновые зубчатые передачи.
Содержание
Конические
зубчатые передачи. Устройство
Геометрические параметры конической
передачи
Силы в зацеплении прямозубой конической передачи
Расчет зубьев прямозубой конической
передачи на изгиб
Расчет конических прямозубых передач на
контактную прочность
Последовательность проектировочного расчета
конической зубчатой передачи
Зубчатые передачи с зацеплением
Новикова. Устройство, основные геометрические соотношения
Достоинства и недостатки передач с
зацеплением Новикова
Расчет передачи с зацеплением Новикова на контактную прочность
Планетарные
зубчатые передачи. Устройство передачи и расчет на прочность
Достоинства и недостатки планетарных
передач
Волновые
зубчатые передачи. Устройство передачи и расчет на прочность
Достоинства и недостатки волновых передач
Передаточное отношение волновых передач
Причины выхода из строя и критерии работоспособности волновых передач
Вопросы для
самопроверки
Конические зубчатые передачи. Устройство.
Зубчатую передачу с пересекающимися осями, у
которой начальные и делительные поверхности колес конические, называют конической.
Коническая
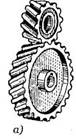
передача состоит из двух конических зубчатых колес (рис. 1) и служит для
передачи вращающего момента между валами с пересекающимися
осями под углом 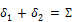 (рис.3). Наиболее распространена в
машиностроении коническая передача с углом
между осями Z=900 (рис. 3), но могут быть передачи и с
(рис.3). Наиболее распространена в
машиностроении коническая передача с углом
между осями Z=900 (рис. 3), но могут быть передачи и с 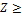 90° до 170°. Пересечение осей валов затрудняет размещение
опор. Одно из колес обычно располагается консольно, что способствует увеличению
неравномерности распределения нагрузки по длине зуба. В коническом зацеплении
действуют осевые силы, наличие которых усложняет конструкцию опор. Все это
приводит к тому, что по опытным данным, нагрузочная способность конической
прямозубой передачи составляет около 0,85 цилиндрической.
90° до 170°. Пересечение осей валов затрудняет размещение
опор. Одно из колес обычно располагается консольно, что способствует увеличению
неравномерности распределения нагрузки по длине зуба. В коническом зацеплении
действуют осевые силы, наличие которых усложняет конструкцию опор. Все это
приводит к тому, что по опытным данным, нагрузочная способность конической
прямозубой передачи составляет около 0,85 цилиндрической.
Колеса
конических передач выполняют с прямыми
(рис. 2, а), косыми (рис. 2, б), круговыми зубьями (рис. 2, в). При окружных скоростях
до 2… 3 м/с применяют
конические колеса с прямыми зубьями, при больших скоростях используют колеса с
круговыми зубьями, которые обеспечивают более плавное зацепление и имеют
большую нагрузочную способность и проще в изготовлении.

Рис. 1. Коническая
прямозубая
передача
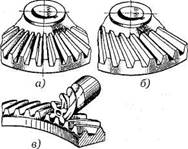
Рис. 2.
Конические зубчатые колеса: а — колесо
с прямыми зубьями;
б — колесо с
косыми зубьями; в —
колесо с круговыми зубьями
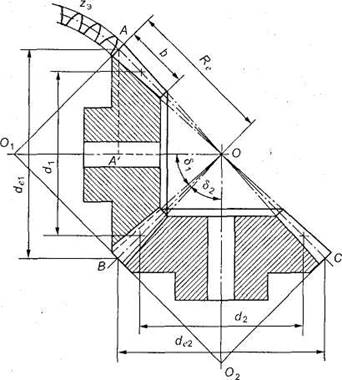
Рис. 3. Геометрические
параметры конических зубчатых колес
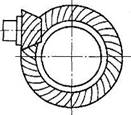
Рис. 4. Гипоиднаяя передача
Передачу с
коническими колесами для передачи вращающего
момента между валами со скрещивающимися
осями называют гипоидной (рис. 4). Эта передача находит применение в автомобилях.
По стоимости конические передачи дороже цилиндрических при равных силовых
параметрах. Их применение диктуется только
необходимостью передавать
момент при пересекающихся осях валов. Передаточное число одной пары u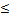 6,3.
6,3.
Геометрические
параметры конической передачи
Вершины
начальных и делительных конусов конической передачи находятся в точке пересечения осей валов О (рис.
5). Высота и толщина зубьев
уменьшаются по направлению к вершинам конусов. Геометрические параметры конической передачи (рис. 3
и 5):
АОВ —
делительный конус шестерни;
ВОС —
делительный конус колеса;
АО1В — делительный дополнительный конус шестерни;
ВО2С —
делительный дополнительный конус колеса;
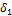 — угол делительного конуса шестерни;
— угол делительного конуса шестерни;
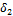 — угол делительного конуса колеса;
— угол делительного конуса колеса;
de1 —
внешний делительный диаметр шестерни;
de2 — то же, колеса;
d1 —
средний делительный диаметр шестерни;
d2 — то же, колеса;
b — ширина зубчатого венца (длина зуба);
Re — внешнее делительное конусное расстояние (или длина дистанции).
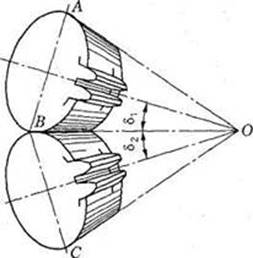
Рис. 5. Коническая прямозубая передача
Передаточное
число конической передачи определяется так:
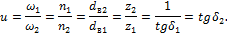
В конической передаче может быть бесчисленное множество делительных окружностей. Для расчета в машиностроении принимают внешнюю и среднюю делительные
окружности (см. рис. 3).
Из условия, что в конической передаче модуль и делительный связаны теми
же соотношениями, что и в цилиндрических передачах, т.е. d=mz (рис.6), определяют внешний de и средний dm делительные диаметры:
dв=mez;
dm=mmz,
где те — внешний окружной модуль; тт — средний окружной
модуль.
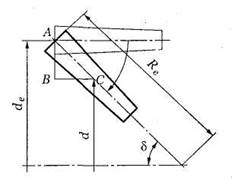
Рис. 6. Зуб конического
колеса
Внешний окружной модуль те обычно
выбирают из стандартного ряда. Округление внешнего модуля до
стандартного значения не является обязательным требованием. Этот модуль называют производственным и по его значению определяют все
геометрические параметры зубчатых колес (задают размеры зубьев на
внешнем торце, на котором удобно производить измерения).
Средний окружной модуль тm рассчитывают в зависимости от внешнего окружного модуля те.
По среднему окружному модулю производят расчет передачи на прочность при изгибе.
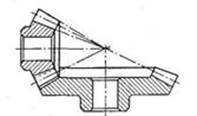
Рис. 7
Зависимость между те и тт в конической
передаче.
Из рис. 6 Re=r+AB, где 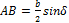 (из
(из 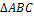 ). Отсюда
Re=r +
). Отсюда
Re=r +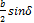 .
.
Умножив левую и правую части равенства на два, получим 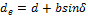 . Разделив левую и правую части равенства
на z, получим
. Разделив левую и правую части равенства
на z, получим
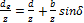 или
me=mm+
или
me=mm+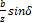
Геометрические
соотношения размеров прямозубой конической передачи с эвольвентным профилем
зуба.
Согласно рис. 8 внешний диаметр вершин зубьев
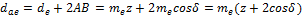
внешний диаметр впадин зубьев
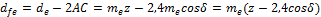
Длина зуба
(ширина венца) 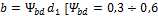 при условии
при условии 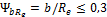 и
и 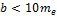 , где d1 — средний делительный
диаметр шестерни].
, где d1 — средний делительный
диаметр шестерни].
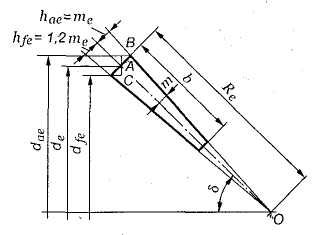
Рис. 8. Геометрия прямозубой конической
передачи
Ориентировочно длина зуба может быть выбрана
также в зависимости от внешнего делительного конусного расстояния Re:
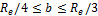 .
.
Таблица 1. Геометрические параметры
прямозубой конической передачи
|
Параметр, обозначение
|
Расчетные формулы
|
|
Внешний окружной модуль me
|
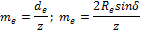
|
|
Средний окружной модуль m
|
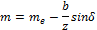
|
|
Внешний диаметр вершин зубьев dac
|
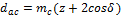
|
|
Внешний делительный диаметр de
|
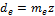
|
|
Внешний диаметр впадин зубьев dfe
|
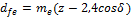
|
|
Высота зуба he
|
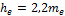
|
|
Высота головки зуба hae
|
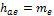
|
|
Высота ножки зуба hfe
|
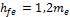
|
|
Окружной шаг pie
|
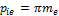
|
|
Окружная
толщина зуба ste
|
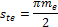
|
|
Окружная
ширина впадины ete
|
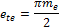
|
|
Радиальный
зазор ce
|
ce=0,25mc
|
|
Ширина
зубчатого венца b
|
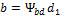
|
|
Внешнее делительное
конусное
расстояние Re
|
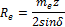
|
|
Угол делительного конуса:
шестерни 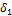
|
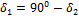
|
|
колеса
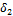
|
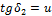
|
Силы в
зацеплении прямозубой конической передачи
В рассматриваемой
передаче действует одна сила, обусловленная давлением зуба шестерни на зуб колеса. Эта сила для удобства
расчетов раскладывается на 3 составляющие: окружная Ft, радиальная Fr и осевая Fa.
С учетом геометрических соотношений в конической передаче по нормали к зубу действует сила Fn1 (рис. 9). Эту силу разложим на две составляющие: 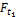 и
и 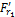 . В свою очередь
. В свою очередь 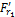 разложим на
разложим на 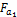 и
и 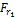 . Запишем:
. Запишем:
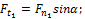
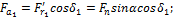
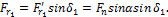
Осевая сила на шестерне численно равна радиальной силе на колесе.
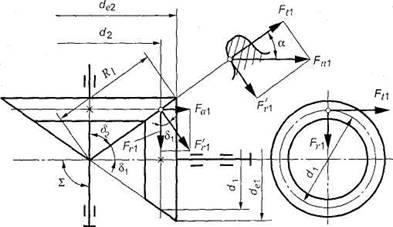
Рис. 9. Силы в зацеплении прямозубой
конической передачи
Рис.10
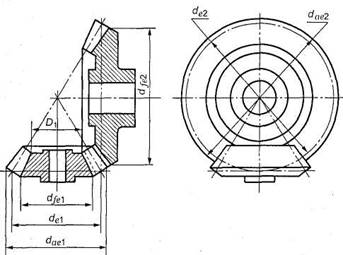
Рис. 11
Расчет
зубьев прямозубой конической передачи на изгиб
Расчет производят по аналогии с расчетом
цилиндрической прямозубой передачи.
Опытным путем установлено, что нагрузочная способность
конической передачи ниже, чем цилиндрической. В соответствии с этим в расчетные формулы для зубьев
конической передачи вводят коэффициент КFO, учитывающий снижение их нагрузочной способности по
сравнению с зубьями цилиндрических передач.
Расчет
на прочность зубьев при изгибе производят по среднему
значению модуля зубьев т. Коэффициент формы зуба YF выбирают по аналогии с цилиндрической прямозубой передачей,
но в зависимости от числа зубьев эквивалентных колес zV=z/cos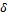 .
.
Под числом зубьев zV эквивалентных колес
понимают такое число зубьев, которое может расположиться на длине окружности
(см. рис. 3) радиусом, равным длине образующей дополнительного конуса О1А.
Проверочный расчет следует проводить по
аналогии с прямозубой передачей.
Расчетные напряжения изгиба в зубьях конических колес и условие прочности выражаются
формулой
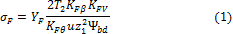
где 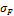 — возникающее
напряжение изгиба, МПа; T2 — вращающий момент на колесе, Нмм;
— возникающее
напряжение изгиба, МПа; T2 — вращающий момент на колесе, Нмм;
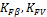 — коэффициенты
нагрузки;
— коэффициенты
нагрузки; 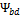 — коэффициент
длины зуба; YF —
коэффициент формы зуба (выбирают по табл. 8) в зависимости от zV;
z1 — число зубьев шестерни; и — передаточное число;
— коэффициент
длины зуба; YF —
коэффициент формы зуба (выбирают по табл. 8) в зависимости от zV;
z1 — число зубьев шестерни; и — передаточное число; 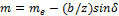 — средний
модуль, мм;
— средний
модуль, мм; 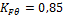 — опытный коэффициент снижения нагрузочной
способности;
— опытный коэффициент снижения нагрузочной
способности; 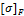 — допускаемое
напряжение изгиба, МПа.
— допускаемое
напряжение изгиба, МПа.
Проектировочный
расчет. Средний модуль зубьев определяется по формуле
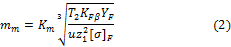
где т, мм; Т2, Нмм; 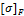 , МПа; Кт= 1,45 — вспомогательный
коэффициент для стальных прямозубых конических колес;
, МПа; Кт= 1,45 — вспомогательный
коэффициент для стальных прямозубых конических колес; 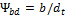 принимают
принимают
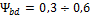 .
.
Расчет
конических прямозубых передач на контактную прочность
В основу данного расчета берется формула (20) в параметрах эквивалентной цилиндрической
прямозубой передачи по среднему дополнительному конусу
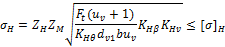
Используем связь тригонометрических функций для
определения передаточного числа и делительного диаметра эквивалентного колеса
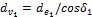 .
.
После подстановки в исходную формулу значений 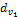 и
и 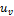 и несложных преобразований получим формулу проверочного
расчета для стальных прямозубых конических колес
и несложных преобразований получим формулу проверочного
расчета для стальных прямозубых конических колес
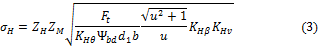
или, заменив 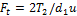 ;
; 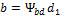 , получим:
, получим:
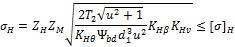
Z=ZH ZM=462
ZM=462 103Па1/2
(для стальных колес), (4)
103Па1/2
(для стальных колес), (4)
где 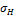 — возникающее нормальное контактное напряжение, МПа; d1 — средний
делительный диаметр шестерни, мм; T2 — вращающий момент на колесе, Нмм;
ZH —
коэффициент, учитывающий форму сопряжения поверхности зубьев; ZM — коэффициент,
учитывающий механические свойства материала; Ψbd —
коэффициент ширины (длины) зуба; u — передаточное число; KHθ = 0,85 — коэффициент, учитывающий снижение контактной
прочности конической передачи по сравнению с прямозубой;
— возникающее нормальное контактное напряжение, МПа; d1 — средний
делительный диаметр шестерни, мм; T2 — вращающий момент на колесе, Нмм;
ZH —
коэффициент, учитывающий форму сопряжения поверхности зубьев; ZM — коэффициент,
учитывающий механические свойства материала; Ψbd —
коэффициент ширины (длины) зуба; u — передаточное число; KHθ = 0,85 — коэффициент, учитывающий снижение контактной
прочности конической передачи по сравнению с прямозубой; 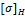 — допускаемое контактное напряжение. Из двух значений
— допускаемое контактное напряжение. Из двух значений 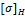 выбирается меньшее.
выбирается меньшее.
Проектировочный
расчет.
Решая уравнение (31) относительно d1 запишем
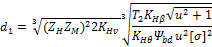
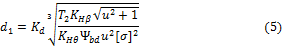
где 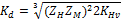 — вспомогательный коэффициент (для стальных
прямозубых конических колес Kd =78 МПа1/3).
— вспомогательный коэффициент (для стальных
прямозубых конических колес Kd =78 МПа1/3).
Последовательность
проектировочного расчета конической зубчатой передачи
Последовательность расчета закрытой передачи.
1. Определить передаточное число u и углы делительных конусов шестерни
и колеса 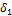 и
и 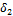 .
.
2. В зависимости от условий работы передачи
выбрать материалы колес, назначить термическую обработку и значения твердости
рабочих поверхностей зубьев.
3. Определить базовое число циклов NHO, расчетную циклическую долговечность NH, коэффициенты режима,
допускаемые контактные напряжения и допускаемые напряжения изгиба.
4. Выбрать коэффициент 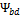 длины зуба.
длины зуба.
5. Определить средний делительный диаметр из
условия контактной прочности [формула (5)].
6. Задать число зубьев шестерни z1, определить число
зубьев колеса z2
7. Рассчитать внешний модуль mв, и округлить его до стандартного значения (см.
табл. 3), а также средний модуль m=mв-(b/z)sin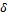 .
.
8. Определить числа зубьев эквивалентных колес zV1 и zV2 и по
табл. 8 — коэффициенты формы зуба шестерни YF1 и колеса YF2.
9. Проверить прочность зубьев по напряжениям
изгиба. При неудовлетворительных результатах (σF>[σ]F) необходимо путем соответствующего изменения числа зубьев
и модуля при том же конусном расстоянии добиться определенного изменения
напряжений изгиба, не нарушая при этом условия контактной
прочности.
10. Произвести геометрический расчет передачи
(см. табл. 1).
11. Определить окружную скорость колес и по табл.
14 назначить соответствующую степень точности.
Последовательность расчета открытых конических передач.
1. Определить передаточное число u и углы γ делительных конусов шестерни и колеса 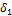 и
и 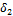 ..
..
2. В зависимости от условий работы передачи выбрать
материалы колес, назначить термическую обработку и значения твердости рабочих
поверхностей зубьев.
3. Определить базовое число циклов NHO, расчетную
циклическую долговечность, коэффициенты режима и определить допускаемые
напряжения изгиба.
4. Задать
число зубьев шестерни z1 и по передаточному числу u определить число зубьев колеса z2.
5.
Определить число зубьев эквивалентных колес zV1 и zV2 и по табл. 8 — коэффициенты формы зуба
шестерни YF1 и колеса YF2.
6. Выбрать коэффициент длины зуба (ширины венца) 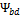 .
.
7. Из условия прочности на изгиб (формула 1) определить
средний модуль mm, после чего
подсчитать внешний модуль mв, значение которого округлить до ближайшего большего
стандартного (см. табл. 3). При необходимости следует пересчитать mm в зависимости от стандартного mв.
8.
Произвести геометрический расчет передачи (см. табл. 1).
9.
Определить окружную скорость колес и по табл. 14 назначить соответствующую
степень точности зацепления.
Зубчатые передачи с зацеплением Новикова. Устройство, основные геометрические соотношения
Классическая эвольвентная
система зацепления, созданная в России академиком Д. Эйлером в 1754 г.,
благодаря своим бесспорным достоинствам заняла господствующее положение в
современной технике. Вместе с тем, как и все системы с линейчатым контактом,
она имеет серьезные органически ей присущие недостатки. Основными из них
являются:
- высокие контактные напряжения в зубьях. Они велики
потому, что контактируют два зуба с выпуклыми профилями. При этом площадка
контакта очень мала, а контактные напряжения соответственно высоки. Это
обстоятельство сильно ограничивает "несущую способность" передач,
т.е. не позволяет передавать большие вращающие моменты.
- ограниченная контактная прочность зубьев, которая,
как известно, зависит от радиусов кривизны профилей зубьев (в случае эвольвентного зацепления при заданных параметрах зубчатых
колес существенно изменить величину этих радиусов невозможно),
- большая чувствительность к перекосу осей валов передачи
(это вызывает трудности обеспечения линейчатого контакта сопряженных
поверхностей зубьев),
- сравнительно большие потери мощности (0,5 … 1,0%) за
счет трения в зацеплении для одной пары зубчатых колес.
Перечисленные недостатки существенно уменьшены в
системе точечного зацепления с круто винтовыми зубьями, предложенной в 1954 г. M.JI.
Новиковым. За свои работы в этой области М.Н. Новикову в 1954 г. присуждена
Ленинская премия.
Благодаря своим достоинствам, передачи Новикова получали
широкую известность не только в Советском Союзе, но и зарубежом.
Так в начале 60-х годов многие капиталистические фирмы
("Фиат", "Виккерс", "Юнсон" и др.) изъявили желание приобрести лицензии на
передачи Новикова.
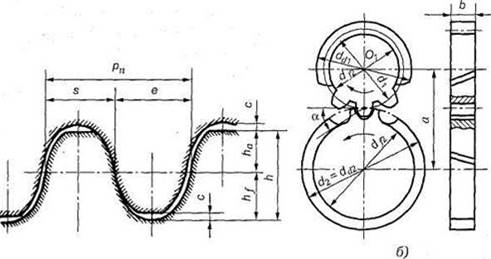
Передачи с зацеплением Новикова состоят из двух цилиндрических косозубых колес (рис. 12, а) или
конических колес (рис. 12, б) с винтовыми
зубьями и служат для передачи момента между валами с параллельными или пересекающимися осями.
Особенность зацепления Новикова состоит в том, что в этом зацеплении первоначальный линейный контакт (рис. 12, в) заменен точечным, превращающимся
под нагрузкой в контакт с
хорошим прилеганием (рис.12, г). Простейшими профилями зубьев, обеспечивающими такой контакт, являются
профили, очерченные по дуге окружности или близкой к ней кривой.
 б)
б)
в)
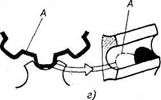
Рис. 12. Передача с
зацеплением М. Л. Новикова. А - площадка
контакта
Обычно профиль зубьев шестерни делается выпуклым, а профиль зубьев колес вогнутым или наоборот
(рис.13, а, б), но могут быть передачи и с профилем зубьев шестерни и колеса, показанным на рис.13,
в. Выпуклый и
вогнутый профили (обычно круговые) имеют близкие по абсолютной величине радиусы
кривизны. За счёт этого получается большая площадка контакта, контактные
напряжения уменьшаются и появляется возможность
передавать примерно в 1,4-1,8 раза
большие вращающие моменты. Торцовое перекрытие, а также геометрическое
скольжение зубьев в передаче Новикова теоретически отсутствует, плавность
работы обеспечивается за счёт осевого перекрытия 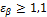 . Угол наклона зубьев обычно берется в пределах β=10°…24°.
. Угол наклона зубьев обычно берется в пределах β=10°…24°.
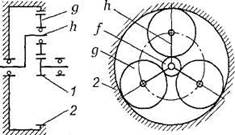
Рис.15. Планетарная передача
Водило вместе с сателлитами
вращается вокруг центральной оси, а сателлиты
обкатываются по центральным колесам и вращаются вокруг своих осей, совершая
движения, подобные движению планет. При неподвижном колесе 2 движение
передается от колеса 1 к водилу h или
наоборот.
Простейшая планетарная передача обычно включает одно солнечное колесо, один
эпицикл и одно водило. Такую планетарную передачу принято называть простым планетарным
рядом.
Главной кинематической характеристикой простого планетарного ряда является
его кратность K=z3/z1; где z3 – количество зубьев
эпицикла; а z1
– количество зубьев солнечного колеса. По количеству планетарных рядов планетарные
передачи бывают одно-, двух-, трёх-, четырех- и многорядные. В российской
литературе часто используют классификацию планетарных передач, предложенную
проф. В.Н. Кудрявцевым. По этой классификации число центральных колёс
обозначается цифрой и буквой K, далее в обозначении передачи через тире указывается
число водил, равное количеству планетарных рядов, и буква H. Согласно этой классификации
представленная на рис. 15 кинематическая схема будет соответствовать передаче 2К-Н.
Планетарный ряд, у которого ни одно из звеньев не соединено со стойкой,
обладает двумя степенями свободы, то есть требует для однозначного характера
движения всех своих звеньев подвода движения извне к двум из этих звеньев.
Такой механизм принято называть дифференциальным. Если же в планетарном
дифференциальном механизме одно из звеньев соединить со стойкой (сообщить ему
постоянную скорость вращательного движения равную 0 радиан в секунду), то такой
механизм превращается в передачу. Связывание со стойкой (или между собой)
разных звеньев дифференциального планетарного ряда ведёт к изменению передаточного
числа планетарной передачи. Применив этот приём к простому планетарному ряду,
можно получить, по крайней мере, 7 вариантов передачи с различными
передаточными отношениями, представленными в таблице 4.
Таблица 8.1.Варианты передаточных
отношений простого планетарного ряда (рис. 15)
|
№ п/п
|
№ входного
звена
|
№ выходного
звена
|
№ заторможенного
звена
|
Передаточное
отношение i
|
|
1
|
1
|
3
|
H
|
-K
|
|
2
|
1
|
H
|
3
|
1+K
|
|
3
|
3
|
1
|
H
|
-K-1
|
|
4
|
3
|
H
|
1
|
1+K-1
|
|
5
|
H
|
1
|
3
|
(1+K)-1
|
|
6
|
H
|
3
|
1
|
(1+K-1)-1
|
|
7
|
1
|
H
|
-
|
1
|
|
Примечание: Вариант 7
соответствует непосредственному соединению
входного и выходного звеньев механизма.
|
Данные таблицы 4 показывают, что использование простого
планетарного ряда в качестве коробки передач транспортного средства позволяет
получить 5 различных скоростей вперёд и 2 – назад при кратности изменения
скоростей: вперёд KV=(1+K)2, назад KV=K2.
Планетарную передачу успешно применяют в
транспортном машиностроении, станкостроении, приборостроении.
Достоинства
и недостатки планетарных передач
Основное
достоинство — широкие кинематические возможности, позволяющие
использовать передачу в качестве редуктора коробки скоростей, передаточное
число в которой изменяется путем поочередного торможения различных звеньев, и
как дифференциальный механизм.
- Планетарный принцип позволяет получать большие
передаточные числа (до тысячи и больше) без применения многоступенчатых
передач.
- Эти передачи удобно компоновть
благодаря соосности ведущего и ведомого валов.
- Эти передачи компактные и имеют малую массу.
Переход от простых передач к планетарным позволяет во
многих случаях снизить их массу в 4 раза и более. Мощность передается несколькими потоками (3
сателлита), при этом нагрузка на зубья уменьшается. Кроме того, внутреннее
зацепление обладает повышенной нагрузочной способностью (у него больший радиус
кривизны).
- Сателлиты в планетарной передаче расположены
симметрично, а это снижает нагрузки на опоры (силы в передаче взаимно
уравновешиваются), что приводит к снижению потерь и упрощает конструкцию опор.
- Эти передачи работают с
меньшим шумом, чем обычные зубчатые и имеют более лёгкое управление и
регулирование скорости;
- Имеют малый шум вследствие замыкания сил в механизме;
- Имеют высокую надежность работы (сохранение
работоспособности даже при потере нескольких зубьев на центральных колёсах);
- Имеют высокий КПД при относительно больших
передаточных числах;
-
Отсутствие поперечной нагрузки на основных валах;
-
Возможность изменения передаточного числа без вывода зубчатых колёс из
зацепления;
-
Возможность отсоединения вала двигателя от трансмиссии при использовании
фрикционов коробки передач (коробка передач одновременно выполняет
роль главного фрикциона);
-
Высокую скорость переключения передач, что способствует повышению среднего
темпа движения машины.
Основные недостатки:
- повышенные требования к точности изготовления и монтажа (для
обеспечения сборки планетарных передач необходимо соблюдать условие соосности
(совпадение геометрических центров колёс);
- условие сборки (сумма зубьев центральных колёс кратна
числу сателлитов) и соседства (вершины зубьев сателлитов не соприкасаются друг
с другом);
- резкое снижение КПД
передачи с увеличением передаточного отношения.
Как правило, планетарные передачи, имеющие в своём
составе эпициклические колёса, отличаются более высоким КПД по сравнению с передачами,
состоящими только из колёс внешнего зацепления. Именно поэтому в планетарных
коробках передач используются простейшие планетарные ряды с эпициклом. Число
переключений в одном ряду обычно не превосходит трёх с целью упрощения системы
управления фрикционами и тормозами. Количество планетарных рядов в одной коробке
передач тоже обычно не бывает более трёх.
Особенности проектирования и расчёта планетарных
передач связаны с наличием избыточных кинематических связей (нескольких
сателлитов). Предельно возможное число сателлитов в одном планетарном ряду
ограничивается условием соседства,
которое гласит: число сателлитов в планетарном
ряду должно быть таким, чтобы соседние сателлиты не касались друг друга.
Анализ геометрии планетарного ряда позволяет записать для возможного числа
сателлитов ограничение сверху:
при расчёте по солнечному колесу (внешнее зацепление) -
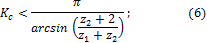
при расчёте по эпициклу (внутреннее зацепление) -
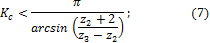
где z1, z2, z3 – числа зубьев солнечного колеса, сателлита и
эпицикла, соответственно, а углы выражены в радианной мере. Но в практике машиностроения
число сателлитов редко принимают более шести в связи с трудностью обеспечения
равномерного распределения нагрузки между ними при большом их количестве.
Второе необходимое условие существования
планетарного ряда называется условием соосности. Суть его вытекает из необходимости соблюдения
соосности центральных колёс, солнечного и эпицикла, и
водила. Для простого планетарного ряда это условие выливается в равенство
межосевых расстояний зацепления солнечного колеса с сателлитом a1-2 и зацепления сателлита
с эпициклом a2-3.
Так как в планетарных рядах применяются преимущественно прямозубые колёса, а в
простом ряду все колёса одного модуля m, можем записать
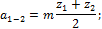
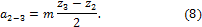
Приравнивая друг другу правые части равенств (8),
получаем
z1 + 2z2
= z3; (9)
после деления обеих частей равенства на z1 имеем
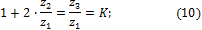
что для передаточного числа между солнечным колесом и
сателлитом даёт
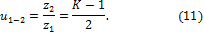
Но, как известно, передаточное число простого
планетарного ряда максимально при ведущем солнечном колесе и ведомом водиле
u1-H = K+1; (12)
и для такой кинематической схемы имеем
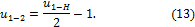
Третье условие диктуется необходимостью равномерного
размещения сателлитов по окружности вокруг солнечного колеса и называется условием сборки. В конечном итоге это
условие выливается в следующее требование: отношение чисел зубьев центральных
зубчатых колёс к числу сателлитов должно быть целым числом или в формульном выражении
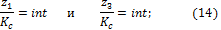
где int
(читается «интегер») – аббревиатура, означающая любое
целое число.
разветвление
потока мощность при передаче силовых нагрузок через сателлиты обусловливает
необходимость принятия специальных мер для обеспечения равномерности
распределения нагрузок между сателлитами. Причин неравномерной загрузки
сателлитов может быть несколько: неточность изготовления зубчатых колёс,
неодинаковость межосевого расстояния у разных сателлитов, перекос
геометрических осей сателлитов (непараллельность осей
сателлитов и главной оси передачи) и др. При необеспечении равномерного
распределения нагрузки между сателлитами расхождение между её величиной у
отдельных сателлитов может достигать до 70 %.
Выравнивание нагрузки между сателлитами может быть
достигнуто путём:
1. повышения точности
изготовления всех деталей передачи;
2. выполнения одного
из центральных колёс или водила плавающим, то есть имеющим некоторую радиальную
подвижность относительно корпуса и сопряжённых деталей;
3. использование
упругих элементов конструкции (обод эпицикла повышенной гибкости, оси
сателлитов малой жёсткости и т.п.).
Прочностной расчёт планетарных передач выполняют по
формулам для цилиндрических передач. При определении расчётного момента, действующего
в зубчатом зацеплении, учитывается число сателлитов, передающих рабочие
нагрузки, и неравномерность нагружения их зубьев. Для
жёсткой передачи без специальных мер выравнивания нагрузки в расчётные формулы
вводят коэффициент неравномерности KH=1,5…2, а при использовании
приёмов, выравнивающих нагрузку на зубьях сателлитов KH=1,1…1,15.
Далее расчёт ведут по наиболее нагруженному зацеплению.
КПД планетарной передачи можно подсчитать по формулам
для передачи с ведущим центральным колесом -
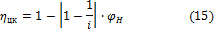
для передачи с ведущим водилом
-
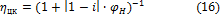
где i – передаточное отношение планетарной передачи, φН – суммарный
коэффициент потерь обращённой передачи (передачи, получающейся из
рассчитываемой при дополнительном сообщении всем её звеньям угловой скорости
равной скорости водила и навстречу ей направленной).
В свою очередь
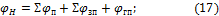
где φп
– потери в подшипниковых узлах передачи (для пары подшипников φп=5∙10-3…1∙10-2);
φзп
– коэффициент потерь в зубчатой паре; φгп=6∙10-3…1∙10-2
– коэффициент, учитывающий затраты энергии на перемешивание смазки.
Потери энергии в зубчатом зацеплении
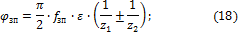
где fзп – коэффициент
трения в зубчатой паре (без смазки fзп≈0,2; со смазкой fзп=0,08…0,15);
ε
– коэффициент окружного перекрытия z1 и z2 – числа зубьев колёс,
входящих в зубчатую пару. В формуле (18) знак «+» принимается
для внешнего зацепления, «-» – для внутреннего.
Для изготовления элементов планетарных передач
используют материалы, предназначенные для рядовых зубчатых передач, это,
главным образом, углеродистые машиностроительные и углеродистые легированные стали,
подвергаемые улучшающей термической обработке.
Как уже упоминалось выше, планетарные механизмы в
исходном состоянии имеют две степени свободы, и это их свойство предопределило
использование этих механизмов в качестве дифференцирующих (суммирующих). В
режиме дифференциала работают планетарные суммирующие механизмы автомобильных
дифференциалов с коническими колёсами, планетарные механизмы поворота
гусеничных машин (танков, гусеничных тягачей и т.п.). Так, например, в
многоцелевой гусеничной машине БМП-3 в качестве второго ведущего звена в
механизме поворота используется эпицикл, что обеспечивает возможность изменения
радиуса поворота машины в широких пределах без изменения её скорости движения.
Передаточное
отношение планетарных передач.
Для определения передаточного отношения
планетарной передачи используется метод Виллиса — метод останова водила.
Передаточное отношение планетарной передачи (см.
рис. 15)
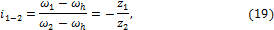
где 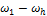 и
и 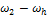 — угловые скорости колес 1
и 2 относительно водила h; z1 и z2 — числа зубьев этих
колес.
— угловые скорости колес 1
и 2 относительно водила h; z1 и z2 — числа зубьев этих
колес.
Для реальной планетарной передачи (колесо 2 закреплено
неподвижно, колесо 1 — ведущее, водило h ведомое) при 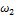 =0 из формулы (36) получим
=0 из формулы (36) получим
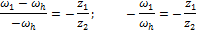
или

Для однорядной планетарной
передачи i1h=1,25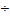 8,0, для
многоступенчатых i1h=30
8,0, для
многоступенчатых i1h=30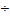 1000, для кинематических передач i1h
1000, для кинематических передач i1h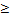 1600. Чем больше
передаточное отношение планетарной передачи, тем меньше КПД (0,99...0,1).
1600. Чем больше
передаточное отношение планетарной передачи, тем меньше КПД (0,99...0,1).
Расчет на контактную прочность зубьев планетарных передач проводится по аналогии с
расчетом обыкновенных зубчатых передач отдельно для каждого зацепления (см.
рис.15): пара колес 1—g (внешнее
зацепление) и g—2
— (внутреннее). Для таких передач достаточно
рассчитать только внешнее зацепление, так как модули и силы в зацеплениях
одинаковые, а внутреннее зацепление прочнее внешнего.
Проектировочный
расчет планетарной передачи на контактную усталость активных поверхностей зубьев проводится по
следующей формуле:
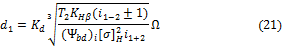
где d1 — делительный диаметр
ведущего звена (шестерни), мм; Kd = 78 МПа — вспомогательный коэффициент (рассматриваются стальные
прямозубые колеса); T2 — вращающий момент на шестерне, Нмм;
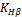 — коэффициент нагрузки;
— коэффициент нагрузки; 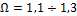 — коэффициент, учитывающий неравномерность
распределения нагрузки среди сателлитов; i1-2 — передаточное отношение;
— коэффициент, учитывающий неравномерность
распределения нагрузки среди сателлитов; i1-2 — передаточное отношение; 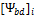 =0,75 — коэффициент длины
зуба (ширины колеса);
=0,75 — коэффициент длины
зуба (ширины колеса); 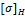 — допускаемое контактное напряжение, МПа.
— допускаемое контактное напряжение, МПа.
При расчете планетарных передач выбор числа
зубьев колес зависит не только от передаточного отношения i, но и от условий собираемости передач. При этом
сумма зубьев центральных колес должна быть кратной числу сателлитов (лучше 3).
Волновые зубчатые передачи. Устройство передачи и расчет на прочность
Волновыми называют
механические передачи, содержащие контактирующие между собой гибкое и жесткое звенья
и обеспечивающие передачу и преобразование движения путем бегущего волнового
деформирования гибкого звена.
В
технике применяется несколько видов волновых передач:
1.
винтовые
волновые передачи, предназначенные для преобразования вращательного движения в
поступательное и/или для передачи этого движения в загерметезированное
пространство;
2.
фрикционные
волновые передачи, предназначенные для преобразования (чаще всего сильного
редуцирования) вращательного движения и/или для передачи этого движения в загерметезированное пространство;
3.
зубчатые
волновые передачи, имеющие аналогичное фрикционным
предназначение, но способные передавать существенно большие мощности.
Принцип использования волновой деформации для передачи
и преобразования движения был предложен инженером А.И. Москвитиным в 1944 году
для фрикционной передачи с электромагнитным генератором волн, а в 1959 году в
США был выдан патент Уолтону Массеру
(Walton Musser) на зубчатую
передачу с механическим генератором волн. В дальнейшем для силовых передач
нашли применение главным образом зубчатые волновые передачи, которые и будут
рассмотрены в настоящем разделе.
Волновой механизм вращательного движения при соответствующем
исполнении может использоваться в качестве редуцирующей передачи,
мультипликатора или дифференциального механизма. Наиболее широкое
распространение получили зубчатые волновые редукторы. Кинематически
волновая передача может быть отнесена к группе планетарных передач, то есть
волновую передачу следует рассматривать как планетарную, у которой одно из центральных
колёс выполнено в форме гибкого зубчатого венца. На
рис. 16 изображены основные элементы волновой передачи: неподвижное колесо 1 с
внутренними зубьями, вращающееся упругое колесо 2 с наружными зубьями и
водило (генератор волн) h. Неподвижное колесо
закрепляется в корпусе и выполняется в виде обычного зубчатого колеса с
внутренним зацеплением. Гибкое зубчатое колесо имеет форму стакана с легко
деформирующейся тонкой стенкой: в утолщенной части (левой) нарезаются зубья,
правая часть имеет форму вала. Водило состоит из
овального кулачка и специального подшипника.
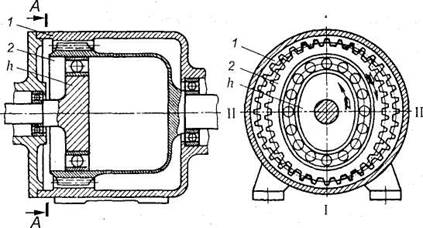
Рис. 16. Волновая
передача
Гибкое колесо деформируется так, что по оси овала
I—I зубья зацепляются на полную рабочую высоту; по оси II—II зубья не зацепляются.
Передача движения осуществляется за счет
деформирования зубчатого венца гибкого колеса. При вращении водила волна
деформации бежит по окружности гибкого зубчатого венца; при этом венец
обкатывается по неподвижному жесткому колесу в обратном направлении, вращая
стакан и вал. Поэтому передача и
называется волновой, а водило — волновым генератором.
При вращении водила овальной
формы образуются две волны. Такую передачу называют двухволновой.
Бывают трехволновые передачи, на рис. 17 показана
схема такой передачи. Но у них выше напряжения изгиба гибкого колеса.
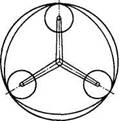
Рис. 17. Трехволновая передача
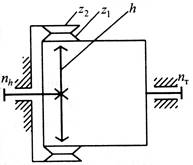
Рис.18. Обозначение волновой передачи на
кинематических схемах
Поскольку передаточное отношение волновой передачи не
зависит от количества волн деформации на гибком колесе, а увеличение числа волн
способствует росту изгибных напряжений в теле гибкого колеса, чаще всего используется
симметричная двухволновая схема деформации гибкого
колеса, позволяющая исключить возможность возникновения поперечных нагрузок на
валах передачи.
В большинстве известных конструкций гибким является
колесо с внешним зубчатым венцом, а жёсткое колесо снабжено внутренними зубьями
(рис. 16). Такая волновая передача включает 3 основных звена: гибкое 1 и жёсткое 2 колёса и генератор волн H. Обычно бывает наиболее удобным конструктивно входной вал
редуктора соединить с генератором волн, а выходной с гибким колесом, в этом
варианте конструкция редуктора получается наиболее компактной и технологичной.
Однако при передаче вращательного движения через герметичную стенку удобнее
гибкое колесо сделать неподвижным, а выходной вал связать с жёстким колесом.
Гибкие колёса силовых редукторов изготавливают из
легированных высокопрочных сталей 30ХГСА; 30ХГСН2А; 40ХНМА; 50С2 и некоторых
других с термообработкой до 38…45 HRC и последующей шлифовкой
диаметра, посадочного на подшипник генератора волн. Для изготовления остальных
деталей применяются те же материалы, что и для рядовых зубчатых передач.
Достоинство и недостатки волновых передач
Достоинства волновых передач:
1. большое
передаточное число (до 320, а в некоторых случаях и более);
2. большое число
зубьев, одновременно находящихся в зацеплении (обычно от 40 до 80%) и, как
следствие этого, большая нагрузочная способность – масса волнового редуктора
меньше массы планетарного той же мощности, а объём может составлять около 30%
от объёма последнего;
3. высокая
кинематическая точность вследствие многозонности и многопарности зацепления, кинематическая погрешность
передачи в некоторых случаях не превышает 0,5 мин;
4. высокий КПД, при
больших передаточных числах превышающий КПД планетарных передач;
5. отсутствие
поперечных нагрузок на валах вследствие симметричности конструкции;
6. возможность
передачи движения в герметизированное пространство;
7. низкий уровень
шума;
8. высокая
вибропрочность за счёт демпфирования (рассеяния
энергии) колебаний (в 4-5 раз больше, чем у обычной зубчатой передачи);
9. возможность
использования в качестве дифференциального механизма;
10. малое
число деталей и относительно низкая стоимость;
11. большая
несущая способность на единицу массы (в 3…4 раза выше, чем у передач зубчатых);
13. надежность
зацепления и малые габариты (при многопарном зацеплении поломка зуба не
нарушает работоспособность и точность передачи);
14. высокая
технологичность изготовления.
Недостатки волновых передач:
1. невозможность
получения низких значений передаточных чисел (для стальных гибких колёс umin≈80, для пластмассовых - umin≈20);
2. необходимость
специального инструмента и оснастки для изготовления гибкого колеса, что
затрудняет индивидуальное производство и ремонт передач;
3. возможность использования этих передач только при
сравнительно невысокой угловой скорости вала генератора;
4. ограниченные обороты ведущего вала (во избежание больших
центробежных сил инерции некруглого генератора волн;
5. мелкие модули зубьев 0,15-2 мм;
6.
сложность конструкции генератора волн;
7. невысокий КПД (в силовых передачах η≈ 0,75…0,9);
8. повышенные
требования к материалу для изготовления гибкого колеса (из-за непрерывного и
значительного деформирования);
9. относительно низкий срок службы (срок
службы стандартных волновых редукторов составляет около 104 часов –
чуть больше года непрерывной работы).
Несмотря на отмеченные недостатки, волновые
передачи все шире применяются в технике и в первую очередь в приводах
летательных аппаратов, луноходах, атомных реакторах, прецизионных приборах,
промышленных роботах. Волновые передачи (с неподвижным гибким колесом) передают
вращение в герметизированное пространство через непроницаемую стенку без
применения уплотнений или специальных диафрагм. Это позволяет применять
передачу в приводах летательных аппаратов и изолированных химически агрессивных
сред. Из-за большой многопарности
зацепления (одновременно в зацеплении находятся 25…30% зубьев гибкого колеса 1) волновая передача позволяет
существенно повысить плавность зацепления, несущую способность и кинематическую
точность. Поэтому волновые передачи в последнее время стали применяться в
приводах промышленных роботов.
Волновые передачи могут работать в качестве редуктора
(КПД 80 – 90%) и мультипликатора (КПД 60 – 70%). В первом случае ведущим звеном является генератор волн, во втором
– вал гибкого или жесткого колеса.
Передаточное отношение волновых
передач
В
недеформированном состоянии гибкое колесо волнового редуктора имеет диаметр и
количество зубьев, меньшие по сравнению с жёстким колесом.
При деформировании волновым генератором гибкое колесо удлиняется в направлении
длинной оси кулачка генератора так, что его зубья входят в контакт с зубьями
жёсткого колеса, вместе с тем вдоль короткой оси кулачка генератора гибкое
колесо сжимается, и его зубья в этом направлении не могут взаимодействовать с
зубьями жёсткого колеса. При вращении кулачка генератора волн последние
пробегают по окружности зубчатого венца гибкого колеса, заставляя тем самым
часть зубьев то входить в зацепление с зубьями жёсткого колеса, то выходить из
него. Если обкатка гибкого колеса по жёсткому происходит без
проскальзывания, то за один оборот генератора ведомое звено повернётся на
угол, соответствующий разности длин окружностей
контактирующих поверхностей жёсткого и гибкого колеса, следовательно,
передаточное число будет равно отношению длины окружности ведомого звена к
разности длин окружностей колёс.
Передаточное отношение
волновых передач определяется методом остановки водила
(метод Виллиса).
При
неподвижном жестком колесе передаточное число волновой передачи определяется
выражением.
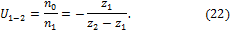
Знак
минус указывает на разные направления вращения ведущего и ведомого звеньев.
При
неподвижном гибком колесе:
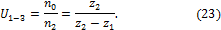
где: n0, n1,
n2 – частота вращения ведущего и ведомых звеньев;
z1,
z2
– числа зубьев гибкого и жесткого колес.
Разность
зубьев жесткого и гибкого колес должна быть равна или кратна числу волн, т.е.:
z1 - z2=Rz,
где: RZ – коэффициент кратности, обычно равный 1,0, но
при U < 70 RZ =
2, а при U
< 45 RZ = 3.
Необходимое
максимальное радиальное перемещение ω0 при отсутствии бокового
зазора (если зубчатые венцы нарезаны без смещения производящего контура) должно
равняться полуразности диаметров начальных
(делительных) окружностей:
nω0 = 0,5(dW1 –
dW2) = 0,5ω(z2
- z1) = 0,5ωRzU.
Разность в числах зубьев жесткого и гибкого колёс с
целью исключения интерференции зубьев должна быть пропорциональна числу волн волнового
генератора.
КПД волновых передач относительно высок и также как в
планетарных передачах падает с увеличением передаточного числа, а с увеличением
нагрузки вначале растёт до максимально возможной величины, а потом, при
дальнейшем возрастании нагрузки, начинает резко снижаться. При оптимальной
нагрузке в пределах передаточного числа 80 ≤ u ≤
250 коэффициент полезного действия 0,9 ≥ h ≥ 0,8.
Иногда применяют в качестве
кинематической волновую передачу с двумя зубчатыми венцами на гибкой оболочке,
соответствующую планетарной с двумя внутренними зацеплениями. КПД такой
передачи низкий – 5%, а передаточное число велико U
= 3600 – 9000.
Причины
выхода из строя и критерии работоспособности волновых передач
Экспериментальные исследования показывают, что волновые
передачи становятся неработоспособными по следующим причинам:
1. Разрушение подшипников генератора волн от нагрузки в
зацеплении или из-за значительного повышения температуры. Повышение температуры
может вызвать недопустимое уменьшение зазора между генератором волн и гибким зубчатым
венцом, что в свою очередь может привести к недопустимому изменению
первоначальной формы генератора волн, гибкого и жесткого зубчатого венцов.
2. Проскок генератора волн при больших крутящих моментах
(по аналогии с предохранительной муфтой). Это явление наступает тогда, когда
зубья на входе в зацепление упираются один в другой поверхностями вершин. При
этом генератор волн сжимается, а жесткое колесо распирается в радиальном
направлении. Для предотвращения проскока радиальное упругое перемещение предусматривают
больше номинального, а зацепление собирают с натягом.
3. Поломка гибкого колеса от трещин усталости, появляющихся
вдоль впадин зубчатого венца, особенно при u < 80. С увеличением толщины гибкого колеса напряжения в
нем от полезного передаваемого момента уменьшаются, а от деформирования генератора
волн уменьшаются. Поэтому есть оптимальная толщина.
4. Износ зубьев на концах;
5. Пластические деформации боковых поверхностей зубьев
при перегрузках.
Анализ причин вывода из строя волновых передач показывает,
что при i > 120 несущая способность обычно ограничивается
стойкостью подшипника генератора волн, при i≤100
– прочностью гибкого элемента. Максимальный допустимый крутящий момент связан с
податливостью звеньев
Основной
причиной выхода из строя волновых передач является поломка гибкого колеса и
гибких колец подшипника генератора волн вследствие усталостного разрушения от
действия знакопеременных изгибающих напряжений. Поэтому размеры передачи
определяют исходя из предела выносливости на изгиб гибкого колеса и наружного
кольца подшипника генератора волн.
Проектным
расчётом определяется внутренний диаметр гибкого колеса по формуле
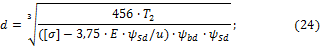
где T1 – вращающий момент на валу гибкого колеса, Н∙м; [σ] - допускаемые
напряжения, МПа (для стали 30ХГСА [𝜎]=150…170
МПа); E - модуль
упругости материала колеса (для сталей можно принять E=2,1∙105 МПа) ψbd=b1/d=0,15…0,20 – коэффициент
ширины зубчатого венца; ψSd=S1/d=0,012…0,014
– коэффициент толщины зубчатого венца.
При
использовании кулачкового генератора волн полученный расчётом диаметр
округляется до ближайшего наружного диаметра гибкого подшипника. Далее
определяются остальные параметры зубчатого зацепления по формулам, аналогичным
с формулами цилиндрических передач.
Рассчитанное гибкое колесо: а) проверяется по напряжениям изгиба,
изменяющимся по симметричному циклу в процессе деформирования колеса
генератором волн; б) по напряжениям растяжения зубчатого венца, возникающим от
действия на колесо тангенциальных сил и изменяющимся по отнулевому
циклу, и по напряжениям кручения зубчатого венца, возникающим при передаче
крутящего момента гибким колесом выходному валу и изменяющимся по отнулевому циклу.
Вопросы для самопроверки
- Какими преимуществами обладают конические
колеса с круговыми зубьями по сравнению с прямозубыми?
- Какими методами производится расчет конических передач?
- В чем разница между направлением сил в конических
передачах прямозубых и с круговым зубом?
- Что такое эквивалентные и биэквивалентные
цилиндрические прямозубые колеса?
- Почему конические передачи с круговым зубом считаются
технологичнее прямозубых?
- В каких случаях применяют конические зубчатые передачи?
- Каковы преимущества косозубых цилиндрических передач по
сравнению с прямозубыми?
- Как влияет на работу косозубой передачи изменение угла
наклона зубьев? Рекомендуемые значения этих углов. Почему ограничивают
максимальное значение угла наклона зуба?
- Какие модули зацепления различают для косозубых колес и
какова зависимость между ними? Какой модуль стандартизован?
- От каких факторов зависят направления окружной и осевой
силы в косозубой передаче?
- Изменение каких параметров
зубчатых колес влияет на их контактную прочность?
- В каких случаях применяют шевронные зубчатые колеса, и
какими достоинствами они обладают по сравнению с
косозубыми? Каковы недостатки шевронных передач?
- Какие рекомендуются углы наклона зубьев шевронных колес и
почему допускается их большая величина, чем у
косозубых?
- Какими достоинствами обладают конические
колеса с круговыми зубьями по сравнению с прямозубыми?
- Является ли модуль зацепления постоянной величиной для
конических зубчатых колес?
- По какому сечению зуба производят расчет на изгиб
конических колес? Какой модуль характеризует размеры этого сечения?
- Как направлены осевые силы, действующие в зацеплении
конических передач?
- Что понимают под эквивалентным цилиндрическим колесом? Как
вычисляют эквивалентные числа зубьев для конических колес и для косозубых
цилиндрических колес?
- Какое минимальное число зубьев допускается для шестерни
цилиндрической и конической передач?
- Какое максимальное передаточное число рекомендуется для
одной пары различных видов зубчатых передач?
- В чём заключаются достоинства и недостатки планетарных
передач?
- Для чего созданы волновые передачи и в чём заключается
принцип их работы?
- В чём заключаются достоинства и недостатки волновых
передач?
- Чем волновые передачи отличаются от планетарных?
- От чего зависит передаточное отношение волновых передач?
- В каком случае входной и выходной валы волновой передачи
вращаются в разные стороны?
- Какое колесо является ведомым при передаче вращения через
герметичную стенку?
- Что такое гибкий подшипник?
- Какая деталь волновой передачи наиболее уязвима?
- Какой формы зубья у волновых передач?
- Каковы устройство и принцип действия волновой передачи?
- От каких параметров зависит передаточное отношение
волновой передачи и чем ограничиваются его max и min?
- Каковы особенности преобразования
движения в зубчатой и фрикционной волновых передачах?
- По каким условиям выбирают профиль и размеры зубьев в
волновой передаче?
- Каковы основные критерии работоспособности и расчета
волновых передач?
- Каковы преимущества и недостатки волновых передач и
области их применения?
- Как устроена и как
работает волновая зубчатая передача?
Назовите основные элементы передачи?
- Каковы основные достоинства и недостатки волновой передачи
по сравнению с другими передачами?
- Каким образом гибкому колесу придают овальную форму? Как
происходит передача движения в волновой передаче от ведущего звена к ведомому?
- Какова разность чисел зубьев жесткого и гибкого колес
волновой передачи? Какой применяют профиль зубьев?
- Как вычисляют передаточное число волновой передачи?
- Почему подшипник кулачкового генератора называют гибким?
- Почему волновые передачи применяют в устройствах с
повышенными требованиями к кинематической точности или к герметичности?
- Сравните
волновую передачу с обычной зубчатой с точки зрения коэффициента перекрытия
зубьев.
- Влияет ли на работоспособность
волновой передачи точность изготовления деталей генератора волн?
- Для чего созданы зацепления Новикова и в чём заключается
принцип конструкции их зубьев?
- В чём заключаются достоинства и недостатки зацеплений
Новикова?
- Назовите достоинства и недостатки зубчатой передачи с
зацеплением Новикова и сравните с зубчатой передачей с эвольвентным
зацеплением?
- Планетарные передачи — устройство и кинематика, оценка и
применение?
- Силы в зацеплении планетарной передачи и особенности
расчета на прочность?
- По каким условиям выбирают числа зубьев колес планетарной
передачи?
- Какую зубчатую передачу называют планетарной? Ее
устройство и принцип работы?
- В каком случае планетарную передачу называют
дифференциальной?
- Каковы основные достоинства и недостатки планетарных
передач по сравнению с обычными зубчатыми?
- В каких областях машиностроения широко применяют
планетарные передачи и почему?
- Какой метод применяют при выводе формулы для определения
передаточного числа планетарной передачи?
- В чем заключаются условия соосности, сборки и соседства
планетарных передач? Почему расчет планетарных передач начинают с подбора чисел
зубьев?
- По какой частоте вращения вычисляют окружную скорость для назначения
степени точности передачи и выбора коэффициентов KHυ
и KFυ?
- Что учитывает коэффициент YA в формуле определения
допускаемых напряжений изгиба для зубьев сателлита?
- Почему в планетарном редукторе центральная шестерня
выполнена плавающей?
- Каковы особенности различных типов планетарных передач?
- Почему КПД планетарных передач увеличивается при
стремлении передаточного отношения к единице?
- Какие из планетарных передач имеют максимальное
передаточное отношение?
- С какой целью применяется самоустановка
колес планетарной передачи?
- Что такое дифференциальная передача и каковы ее
особенности?
- Какие опоры планетарных передач нагружены больше всего и
почему?
- Какой параметр планетарной передачи определяется при
проектном расчете? Какое передаточное число используется при этом?
- Каковы условия собираемости планетарных передач?
- Сколько степеней точности зубчатых передач и какова их
зависимость от окружных скоростей?
- В чем состоит модификация зубчатых зацеплений?
- Какие виды модификаций применяют в цилиндрических и
конических зубчатых передачах?
- Каковы материалы и виды термообработки для цилиндрических
и конических зубчатых колес?
- Каковы способы изготовления конических зубчатых передач?
- Основное конструктивное отличие
зуба Новикова от известных.
- Перечислите недостатки и
основные достоинства зубчатых передач с зацеплением Новикова.
- Вспомните формулы расчета на
контактную прочность цилиндрической эвольвентной
прямозубой передачи.
- Какие профили зубьев применимы
для планетарной зубчатой передачи?
- Перечислите примеры возможного
применения планетарных передач.
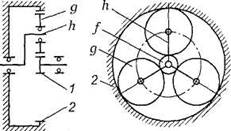
- Объясните, почему для
планетарной передачи (см. рис.)
достаточно рассчитать только внешнее зацепление?
- Конические зубчатые передачи, их оценка по сравнению с цилиндрическими? Области применения? Основные геометрические
параметры конической передачи?
- Силы в зацеплении прямозубой конической передачи?
- Приведение конического зубчатого колеса к эквивалентному цилиндрическому (эквивалентные параметры dv и zv)?
- Чем отличаются расчетные формулы для σH и σF в конических передачах по сравнению с цилиндрическими и почему?
- Какие формы непрямых зубьев применяют в конических
передачах и как оценивают их преимущества в расчетных зависимостях для σH и σF?
- По каким критериям распределяют передаточное отношение по
ступеням многоступенчатой передачи?
- Какие потери определяют КПД зубчатой передачи, и какова
его приближенная величина?
- Какие материалы и виды термической обработки применяют для
повышения прочности и долговечности зубчатых передач?
- От каких характеристик материала преимущественно зависят
сопротивление контактной усталости и допускаемые контактные напряжения?
- Как учитывают переменность режима нагрузки при определении
допускаемых напряжений?
- Как записывают условие суммирования повреждений и как его
объясняют?
- Что такое типовые режимы нагружения?
- По каким параметрам оптимизируют конструкцию зубчатых
передач? Что принимают за обобщенный критерий оптимизации?
- Какие из цилиндрических и конических зубчатых передач
применяют для передачи вращения между валами, оси которых скрещиваются?
- Ниже перечислены основные передачи зубчатыми
колесами:
а) цилиндрические
с прямым зубом;
б) цилиндрические
с косым зубом;
в) цилиндрические
с шевронным зубом;
г) конические
с прямым зубом;
д) конические
с косым зубом;
е) конические
с круговым зубом;
ж) цилиндрическое колесо и
рейка.
Сколько из них могут быть
использованы для передачи вращения между пересекающимися осями?
1. Одна.
2. Две.
3. Три.
4. Четыре.
- Сравнивая зубчатые передачи с
другими механическими передачами, отмечают:
а) сложность изготовления и
контроля зубьев;
б) невозможность проскальзывания;
в) высокий КПД;
г) малые габариты;
д) шум при работе;
е) большую долговечность и
надежность;
ж) возможность применения в
широком диапазоне моментов, скоростей, передаточных отношений.
Сколько из перечисленных свойств
можно отнести к положительным?
1. Три.
2. Четыре.
3. Пять.
4. Шесть.
- Чтобы зубчатые колеса могли
быть введены в зацепление, что у них должно быть одинаковым?
1. Диаметры.
2. Ширина.
3. Число
зубьев.
4. Шаг.
- Механизм имеет несколько последовательных
передач; при вращении ведущего вала со скоростью 1000 об/мин ведомый вращается со скоростью 80 об/мин. Как правильно
назвать этот механизм?
1. Коробка скоростей;
2. Вариатор;
3. Мультипликатор;
4. Редуктор.
- По какому принципу построены
ряды стандартных значений межосевых расстояний, передаточных чисел,
коэффициента ширины зубьев?
1. Ряд
целесообразных чисел.
2.
Арифметическая прогрессия.
3.
Геометрическая прогрессия.
4.
Логарифмический ряд.
- Диаметр делительной окружности
конического зубчатого колеса, если средний модуль m = 3 мм, число зубьев z = 20, угол делительного конуса 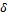 =45° и ширина венца b = 10 мм, равен:
=45° и ширина венца b = 10 мм, равен:
1) 62 мм
2) 67 мм
3) 50 мм
4) 60 мм
5) 70
- Отмечаются особенности передач коническими
зубчатыми колесами по сравнению с цилиндрическими:
1. сложнее в
изготовлении и монтаже;
2. работают с
меньшим шумом;
3.
неравномерность распределения нагрузки по длине зуба больше, так как одно из
колес размещено на консоли вала;
4. позволяют
передавать вращение между пересекающимися валами.
Какая
особенность сформулирована неверно?
- Какая из
формул для определения передаточного числа редуцирующей конической передачи
записана неверно?

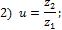
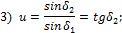
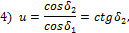
где d1, d2 —
делительные диаметры шестерни, колеса; z1,
z2—числа зубьев; 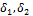 —углы
при вершинах начальных конусов.
—углы
при вершинах начальных конусов.
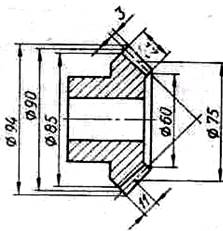
- Какой угол
пересечения осей валов в передачах коническими зубчатыми колесами имеет
наибольшее распространение?
1) 60°;
2) 75°;
3) 90°;
4) 120°.
- Какой формы
не бывают зубья в конических зубчатых колесах?
1. Прямые.
2. Косые.
3. Круговые и
криволинейные.
4. Шевронные.
- На рисунке
изображена шестерня прямозубая коническая с числом зубьев z=30. Чему равен ее модуль?
1. m=3 мм,
2. m=2,5 мм.
3. m=2 мм.
4. m= 1,5 мм.
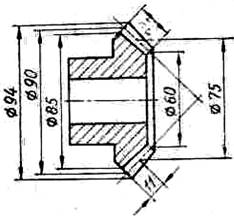
- На рисунке
изображено нормальное прямозубое коническое зубчатое колесо. Сколько у него зубьев?
1) 40;
2) 30;
3) 25;
4) 20.
- Ниже
перечислены основные параметры прямозубого конического зубчатого колеса:
1. модуль (m);
2. число
зубьев (z);
3. конусное
расстояние (Rе);
4. полуугол
начального конуса (δ);
5. диаметр (d2);
6. ширина
зуба (b);
7. угол
профиля зуба 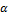 .
.
Сколько из
них должны назначаться из стандартного ряда чисел?
1. Два.
2. Три.
3. Четыре.
4. Пять.
- Какой критерий работоспособности наиболее
вероятен для передач коническими зубчатыми колесами в редукторном исполнении?
1. Изгибная
усталостная прочность зубьев.
2. Изгибная
статическая прочность зубьев.
3. Контактная
усталостная прочность зубьев.
4. Контактная
статическая прочность зубьев.
- Сколько из
перечисленных параметров надо назначить или определить предварительными
расчетами, чтобы выполнить прочностной расчет закрытой конической зубчатой
передачи?
1. Число
зубьев (z1, z2).
2.
Передаточное число (u).
3. Частота
вращения (п1,
n2).
4. Материалы
зубчатых колес пары.
5. Модуль (m).
6. Угол
наклона зуба (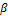 ).
).
7.
Коэффициент ширины зуба (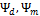 ).
).
8.
Передаваемая мощность (Р).
1) 4;
2) 5;
3) 6;
4) 7.
- Как используют
для расчета передач коническими зубчатыми колесами аналогичные формулы для
расчетов передач цилиндрическими зубчатыми колесами?
1. Принимают
номинальную нагрузку.
2. Завышают
нагрузку.
3. Занижают
нагрузку.
4. Завышают
или занижают в зависимости от конкретных условий эксплуатации.
- Какой
стандартный модуль назначают в передачах с круговыми зубьями?
1. Торцовый на делительном диаметре.
2. Нормальный на среднем диаметре.
3. Торцовый на наименьшем значении диаметра делительного
конуса.
4. Торцовый на среднем диаметре.
- Какие по
направлению силы возникают в зацеплении конических зубчатых колес?
1. Окружная и
радиальная.
2. Окружная и
осевая.
3. Осевая и
радиальная.
4. Окружная,
радиальная, осевая.
- Приведены зависимости для расчета окружной (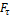 ), радиальной (
), радиальной (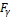 ) и осевой (Fа)
сил в зацеплении конических прямозубых зубчатых колес:
) и осевой (Fа)
сил в зацеплении конических прямозубых зубчатых колес:
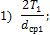
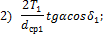
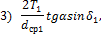
где T1 — момент на шестерне; dср1 — средний диаметр
шестерни; 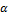 — угол зацепления;
— угол зацепления; 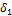 — полуугол начального конуса шестерни.
— полуугол начального конуса шестерни.
По какой
формуле можно определить осевую силу на ведомом зубчатом колесе?
1) такой формулы нет;
2) 1;
3) 2;
4) 3.
- Какой
модуль может быть принят стандартным в
конической передаче?
1. те
2. тт
3. Оба
-
Пользуясь каким модулем рассчитывают диаметр
окружности впадин в конической передаче?
1. те
2. тт
3. те и тт
- Чему
равна высота (мм) головки зуба, если колесо имеет 45
зубьев (см. рис.); de1 = 51 мм, de2 = 225 мм?
1) 3,75
2)
11,25
3) 5,0
4) 6,25
5) По
этим данным нельзя подсчитать
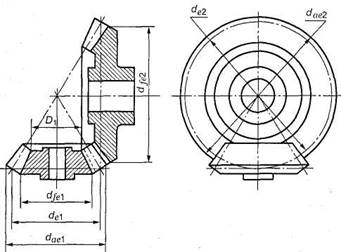
-
Покажите на рисунке диаметр окружности впадин шестерни
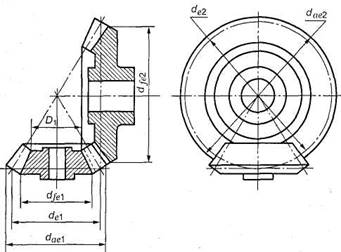
1. dae1
2. de1
3. dfe1
4. D1
- По
какой формуле проводят проверочный расчет закрытых конических передач на
контактную прочность?
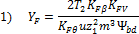
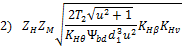
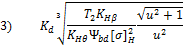
- По
какому модулю ведется расчет конического колеса на изгиб?
1. me
2. m
3.
Можно по me и по m
- Какими могут
быть оси в передаче винтовыми зубчатыми колесами?
1.
Параллельными.
2.
Пересекающимися.
3.
Скрещивающимися.
4. И
параллельными, и пересекающимися, и скрещивающимися.
- Какой формы
зубья у зубчатого колеса гипоидной передачи?
1. Прямые.
2. Косые.
3. Круговые.
4. И прямые, и косые, и
круговые.
- Как
расположены оси ведущего и ведомого элементов в волновых передачах?
1.
Соосно.
2.
Параллельно.
3.
Пересекаются.
4.
Скрещиваются.
- Какие зубья
имеет зубчатое колесо с зацеплением Новикова?
1
Прямые.
2. Винтовые
(косые).
3.
Круговые.
4. Любые из перечисленных.
- Какими
кривыми очерчен рабочий профиль зуба в передаче с зацеплением Новикова?
1.
Эвольвентой.
2. Циклоидой.
3. Дугами
окружности.
4. Сочетанием
прямых и дуг окружности.
- Приведенный
радиус кривизны в зацеплении Новикова по сравнению с эвольвентным:
1. больше;
2. меньше;
3. равен;
4. и больше, и меньше, и равен.
- Во сколько раз
(примерно) несущая способность передач с зацеплением Новикова при улучшенных
материалах зубчатых колес и двух линиях зацепления выше, чем эвольвентных?
1. В 1,1 раза.
2. В 1,4 раза.
3. В 1,8 раза.
4. В 2,2 раза.
- Чему равны
реальные значения угла наклона зубьев у зубчатых колес с зацеплением Новикова?
1) 6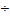 10°;
10°;
2) 10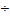 20°;
20°;
3) 20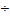 30°;
30°;
4) 30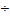 50°.
50°.
- Нагрузочную
способность передачи с зацеплением Новикова можно увеличить:
1. перейдя на профиль с двумя линиями зацепления;
2. искусственно увеличивая число пар зацепляющихся зубьев;
3. уменьшая угол наклона зубьев;
4. увеличивая модуль.
Какой способ
предпочтителен при ограниченных осевых габаритах?
- Принято
различать редукторы:
1)
одноступенчатые;
2)
двухступенчатые;
3)
трехступенчатые;
4)
многоступенчатые.
Какие из них
получили наибольшее распространение в современном машиностроении?
- Какая
передача показана на рисунке?
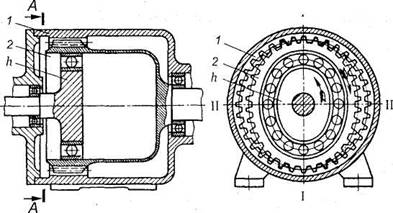
1. Зубчатая с внутренним зацеплением
2.
Зубчатая планетарная
3.
Зубчатая волновая
- Как
называют деталь h на рисунке?
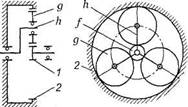
1.
Водило
2.
Сателлиты
-
Покажите на рисунке ведущий вал зубчатой передачи

1) 1
2) 2
3) q
4) h
-
Достаточно привести расчет на контактную прочность зубьев планетарных передач
по рисунку только для зацепления.
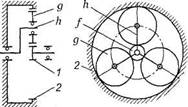
1.
Внешнего
2.
Внутреннего
3.
Внешнего + внутреннего
-
Влияют ли параметры сателлитов в планетарной передаче на значение
передаточного числа
1.
Влияют
2. Не
влияют
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Строительная механика
Теория машин и механизмов
![]() (рис.3). Наиболее распространена в
машиностроении коническая передача с углом
между осями Z=900 (рис. 3), но могут быть передачи и с
(рис.3). Наиболее распространена в
машиностроении коническая передача с углом
между осями Z=900 (рис. 3), но могут быть передачи и с ![]() 90° до 170°. Пересечение осей валов затрудняет размещение
опор. Одно из колес обычно располагается консольно, что способствует увеличению
неравномерности распределения нагрузки по длине зуба. В коническом зацеплении
действуют осевые силы, наличие которых усложняет конструкцию опор. Все это
приводит к тому, что по опытным данным, нагрузочная способность конической
прямозубой передачи составляет около 0,85 цилиндрической.
90° до 170°. Пересечение осей валов затрудняет размещение
опор. Одно из колес обычно располагается консольно, что способствует увеличению
неравномерности распределения нагрузки по длине зуба. В коническом зацеплении
действуют осевые силы, наличие которых усложняет конструкцию опор. Все это
приводит к тому, что по опытным данным, нагрузочная способность конической
прямозубой передачи составляет около 0,85 цилиндрической. 



![]() 6,3.
6,3.![]() — угол делительного конуса шестерни;
— угол делительного конуса шестерни;![]() — угол делительного конуса колеса;
— угол делительного конуса колеса;
![]()


![]() (из
(из ![]() ). Отсюда
Re=r +
). Отсюда
Re=r +![]() .
.![]() . Разделив левую и правую части равенства
на z, получим
. Разделив левую и правую части равенства
на z, получим![]() или
me=mm+
или
me=mm+![]()
![]()
![]()
![]() при условии
при условии ![]() и
и ![]() , где d1 — средний делительный
диаметр шестерни].
, где d1 — средний делительный
диаметр шестерни].
![]() .
.![]() и
и ![]() . В свою очередь
. В свою очередь ![]() разложим на
разложим на ![]() и
и ![]() . Запишем:
. Запишем:![]()
![]()
![]()



![]() .
.![]()
![]() — возникающее
напряжение изгиба, МПа; T2 — вращающий момент на колесе, Нмм;
— возникающее
напряжение изгиба, МПа; T2 — вращающий момент на колесе, Нмм;
![]() — коэффициенты
нагрузки;
— коэффициенты
нагрузки; ![]() — коэффициент
длины зуба; YF —
коэффициент формы зуба (выбирают по табл. 8) в зависимости от zV;
z1 — число зубьев шестерни; и — передаточное число;
— коэффициент
длины зуба; YF —
коэффициент формы зуба (выбирают по табл. 8) в зависимости от zV;
z1 — число зубьев шестерни; и — передаточное число; ![]() — средний
модуль, мм;
— средний
модуль, мм; ![]() — опытный коэффициент снижения нагрузочной
способности;
— опытный коэффициент снижения нагрузочной
способности; ![]() — допускаемое
напряжение изгиба, МПа.
— допускаемое
напряжение изгиба, МПа.![]()
![]() , МПа; Кт= 1,45 — вспомогательный
коэффициент для стальных прямозубых конических колес;
, МПа; Кт= 1,45 — вспомогательный
коэффициент для стальных прямозубых конических колес; ![]() принимают
принимают
![]() .
.![]()
![]() .
.![]() и
и ![]() и несложных преобразований получим формулу проверочного
расчета для стальных прямозубых конических колес
и несложных преобразований получим формулу проверочного
расчета для стальных прямозубых конических колес![]()
![]() ;
; ![]() , получим:
, получим:![]()
![]() ZM=462
ZM=462![]() 103Па1/2
(для стальных колес), (4)
103Па1/2
(для стальных колес), (4)![]() — возникающее нормальное контактное напряжение, МПа; d1 — средний
делительный диаметр шестерни, мм; T2 — вращающий момент на колесе, Нмм;
ZH —
коэффициент, учитывающий форму сопряжения поверхности зубьев; ZM — коэффициент,
учитывающий механические свойства материала; Ψbd —
коэффициент ширины (длины) зуба; u — передаточное число; KHθ = 0,85 — коэффициент, учитывающий снижение контактной
прочности конической передачи по сравнению с прямозубой;
— возникающее нормальное контактное напряжение, МПа; d1 — средний
делительный диаметр шестерни, мм; T2 — вращающий момент на колесе, Нмм;
ZH —
коэффициент, учитывающий форму сопряжения поверхности зубьев; ZM — коэффициент,
учитывающий механические свойства материала; Ψbd —
коэффициент ширины (длины) зуба; u — передаточное число; KHθ = 0,85 — коэффициент, учитывающий снижение контактной
прочности конической передачи по сравнению с прямозубой; ![]() — допускаемое контактное напряжение. Из двух значений
— допускаемое контактное напряжение. Из двух значений ![]() выбирается меньшее.
выбирается меньшее.![]()
![]()
![]() — вспомогательный коэффициент (для стальных
прямозубых конических колес Kd =78 МПа1/3).
— вспомогательный коэффициент (для стальных
прямозубых конических колес Kd =78 МПа1/3). ![]() и
и ![]() .
.![]() длины зуба.
длины зуба.![]() .
.![]() и
и ![]() ..
..![]() .
. б)
б)


![]() . Угол наклона зубьев обычно берется в пределах β=10°…24°.
. Угол наклона зубьев обычно берется в пределах β=10°…24°.