Главная
Раздел 10. Технические приложения теории колебаний
10.1. Основы
расчета виброизоляции
Колебания, возникающие при работе различного рода
машин и механизмов, передаются прилегающим конструкциям и объектам, что
нарушает нормальную работу других устройств, а также вредно влияет на здоровье
человека. Кроме того, часто приходится устанавливать различные приборы и другие
объекты на колеблющемся основании. При этом, как правило, требуется изолировать
объект от основания так, чтобы ему не передавались колебания последнего. В
обоих случаях задача виброизоляции решается одинаково - между объектом и основанием
устанавливают упругие элементы, а иногда и демпферы сухого или вязкого трения.
Рассмотрим
простейшую систему виброзащиты (рис.77,а). Здесь объект массой 
, на который действует гармоническая возмущающая сила 
, соединен с основанием упругой связью с жесткостью 
и элементом вязкого
трения с коэффициентом трения 
.
Выше было установлено, что при колебаниях такой системы перемещения груза меняются по закону:
,
где
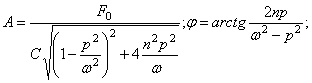
- коэффициент
затухания; 
- частота собственных
колебаний системы.
Рис.77
В задаче расчета
виброизоляции существенными являются не столько перемещения объекта 
, сколько динамическое усилие 
, передаваемое основанию. Это усилие является суммой реакции
упругой связи 
и силы вязкого трения 
:
,
где
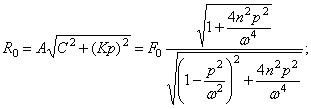
Отношение
амплитуды силы, передаваемой основанию 
, к амплитуде возмущающей силы 
называется коэффициентом виброизоляции 
:
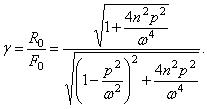(352)
На рис.78
показаны графики зависимости коэффициента виброизоляции 
от отношения частоты возмущающей
силы к собственной частоте системы.
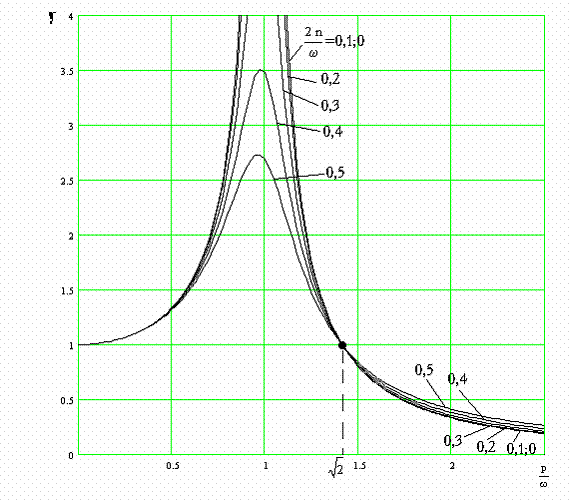
Рис.78
В случае,
если система виброизоляции служит для защиты объекта от передачи ему
колебаний основания (рис.77,б), коэффициентом виброизоляции называется отношение
ускорения объекта к ускорению основания. Этот коэффициент также выражается
формулой (352).
Действительно, уравнение движения объекта (рис.77,б) имеет вид
(353)
где - смещение объекта, 
- смещение основания.
При гармоническом возбуждении смещение основания определяется формулой
а смещение
объекта - 
Подставляя эти значения в (353), получим
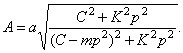
Коэффициент виброизоляции:
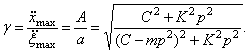
Это выражение полностью совпадает с (352), следовательно, график на рис.78 относится в равной мере к обоим случаям виброизоляции.
Очевидно, что
система виброизоляции эффективна только в том случае, когда отношение 
велико, т.е. если
собственная частота системы мала по сравнению с частотой возмущения. При 
упругая подвеска
приносит не пользу, а вред, так как коэффициент виброизоляции оказывается большим
единицы. Демпфирование ухудшает эффективность виброизоляции в области высоких
частот, но снижает резонансные пики.
Незначительное демпфирование полезно, так как позволяет сохранить продолжительность переходных процессов и ограничить амплитуды при пуске и остановке системы.
Для обеспечения низкой собственной частоты колебаний изолируемого объекта необходимо сделать систему виброизоляции достаточно податливой. Однако при этом возникает опасность излишней подвижности объекта при действии медленно изменяющихся нагрузок. Например, приборы самолетного оборудования, система изоляции которых рассчитана на гашение вибраций, передаваемых от двигателя, могут получать недопустимо большие перемещения при перегрузках, связанных с маневрами самолета. Для ограничения возможных перемещений в этом случае устанавливают упоры (рис.79,а). При наличии упоров система амортизации становится нелинейной (рис.79,б).
В такой нелинейной системе возможны режимы движения с ударами об ограничители, что недопустимо. Для их исключения система виброизоляции должна быть рассчитана на основе нелинейной теории.
Выведем
формулу для определения наименьшего допустимого расстояния до упоров в случае,
если упоры являются весьма жесткими, располагаются симметрично, а удар о них
определяется коэффициентом восстановления скорости 
. Другие виды демпфирования при этом не учитываются.
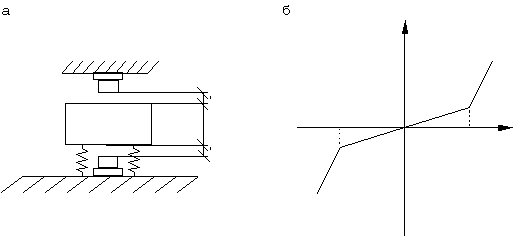
Рис.79
Рассмотрим режим движения, при котором за один период возмущения имеют место удары о верхнюю и нижнюю опоры. Уравнение движения при таком кинематическом возбуждении имеет вид
(354)
где 
- смещение объекта
относительно вибрирующего основания; и 
- абсолютные смещения объекта и основания.
Общее решение уравнения (354) для периода движения объекта между упорами таково:
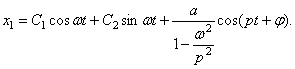(355)
Совместив
начало отсчета времени с моментом отскока объекта от нижнего упора (что всегда
можно сделать, выбрав надлежащим образом фазовый угол 
), имеем
при 
: 
при 
: 
Кроме того, следует учесть условие, связывающее скорость удара об ограничитель со скоростью отскока от него:
.
Три записанных
условия позволяют определить постоянные 
входящие в решение (355). Эти условия приводят
к равенствам:
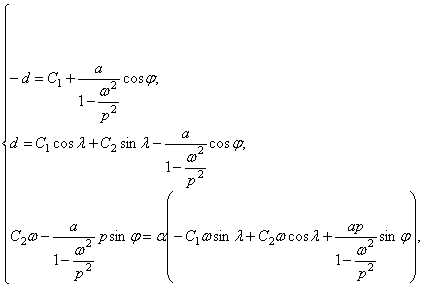
где
Из первых двух уравнений находим
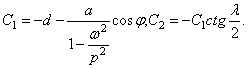
Подстановка этих значений в третье уравнение приводит к соотношению
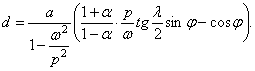(356)
Очевидно, что
стационарный режим движения с ударами об упоры возможен, если можно подобрать
такое значение фазового угла ,
чтобы выполнялось равенство (356). И наоборот, удары об упоры невозможны, если
зазор 
больше, чем максимальное значение правой части
равенства (356).
Таким образом, достаточное условие отсутствия ударов об упоры имеет вид
,
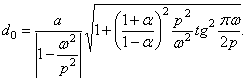(357)
Из (357) следует, что для предупреждения ударов зазор должен быть существенно больше, чем стационарная амплитуда колебаний, рассчитанная по линейной теории:
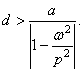
Величина
коэффициента восстановления значительно влияет на размеры необходимого
зазора, поэтому в конструкциях упоров обычно используют материалы с большим
поглощением энергии.
Одним из методов снижения частоты собственных колебаний системы виброизоляции без уменьшения ее жесткости является искусственное увеличение массы объекта.
Полученные выше соотношения для системы с одной степенью свободы справедливы для более сложных систем. Так, для линейно-упругой системы можно ввести главные координаты, и тогда движение по каждой из координат будет определяться самостоятельным уравнением. Наряду с системами, в которых защита от вибраций достигается с помощью пассивных элементов, в ответственных конструкциях используют также системы активной виброзащиты. В этих системах вибрации подавляются за счет энергии постороннего источника, управляемого системой автоматического регулирования.
10.2.
Автоматическая балансировка вращающихся валов
При вращении несбалансированного вала всегда наблюдаются более или менее интенсивные поперечные колебания. Амплитуды колебаний зависят от угловой скорости вращения и при определенных для данного вала критических значениях скорости возрастают столь значительно, что нарушают нормальные условия эксплуатации и могут вызвать поломку вала. При этом критическое состояние нельзя устранить даже самой тщательной балансировкой, поэтому необходимо добиваться, чтобы эксплуатационные угловые скорости не совпадали с критическими.
Рассмотрим
вал, на котором с эксцентриситетом е
насажен диск массой .
Чтобы исключить влияние веса и рассмотреть явление в наиболее чистом виде,
будем считать, что ось вала расположена вертикально (рис.80,а). Вал имеет
круглое сечение и вращается в подшипниках; диск расположен посередине между
опорами.
При вращении
вала с угловой скоростью р центр
тяжести диска будет двигаться по окружности и возникнет центробежная сила.
Обозначим прогиб вала, вызываемый этой силой, через 
, тогда результирующий эксцентриситет равен 
, а центробежная сила - 
. Чтобы определить прогиб , нужно найти отношение центробежной силы к изгибной
жесткости вала с:
или
(358)
т.е. прогиб вала пропорционален начальному эксцентриситету.
Из (358) следует, что критическое состояние наступает
при вполне определенном значении угловой скорости, зависящем от параметров
системы:
(359)
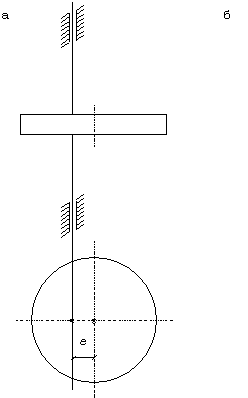
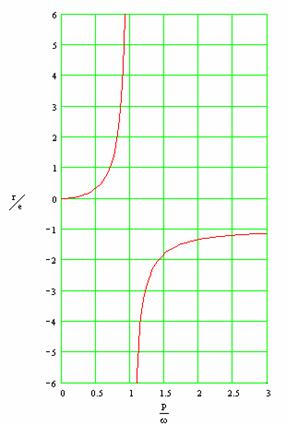
Рис.80
Величину 
называют критической скоростью вращения; она
совпадает с собственной частотой 
невращающейся системы
вал-диск и тем больше, чем жестче вал и легче диск.
Из (359) следует выражение для относительного прогиба вала
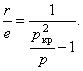(360)
Кривая
зависимости 
приведена на рис.80,б.
Анализ показывает, что при медленном вращении прогибы 
малы и возрастают с
ростом угловой скорости; при этом центр тяжести диска 
расположен дальше от
центра вращения 
, чем центр сечения вала 
(рис.81,а). Если 
, то прогиб равен бесконечности и наступает критическое
состояние.
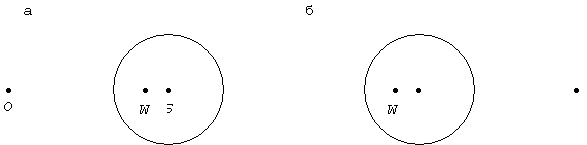
Рис.81
В
закритической области, когда 
, прогибы вновь оказываются конечными, но имеют знак,
противоположный начальному эксцентриситету. На рис.81,б показано
соответствующее этому случаю взаимное расположение центров 
и . При быстром вращении, когда , центр тяжести диска 
оказывается ближе к
центру вращения 
, чем центр вала . Чем больше угловая скорость, тем ближе располагается центр
тяжести диска к центру вращения , а при 
центр тяжести диска
неограниченно приближается к оси вращения. Таким образом, при весьма больших
угловых скоростях происходит самоцентрирование диска. Поэтому, делая вал весьма
гибким, т.е. добиваясь малых значений 
, можно получить хорошую сбалансированность системы. Это
используется при проектировании валов быстроходных турбин, где гибкие валы
оказываются рациональнее жестких.
Ранее критическое
состояние было определено как состояние неограниченного нарастания прогиба
вала, если диск имеет начальный эксцентриситет. Возможна также другая трактовка
критического состояния. Из (358) видно, что если 
и одновременно 
, то прогиб оказывается
неопределенным. Это означает, что при 
полностью
сбалансированный вал теряет устойчивость прямолинейной формы. Если эту форму
нарушить, то вал не стремится ее восстановить, так как упругая реакция 
точно уравновешивается
возникающей при отклонении центробежной силой 
.
При всяком
фиксированном значении угловой скорости (кроме ) вращение сопровождается определенной и неизменной во
времени деформацией вала. Любое волокно в процессе движения остается одинаково
растянутым (или сжатым) независимо от времени.
Критическое
состояние обычно считают недопустимым в эксплуатации, и вблизи выделяют запретную
зону опасных значений угловых скоростей.
Для устранения изгиба, возникающего при вращении неуравновешенного вала, иногда применяют специальные устройства, обеспечивающие автоматическую балансировку. Такая балансировка особенно необходима, когда в условиях эксплуатации возможно существенное изменение несбалансированности вала или ротора. Примером могут служить некоторые типы центрифуг, при загрузке которых возможно значительное нарушение симметрии распределения масс относительно оси вращения.
Автоматическая балансировка способствует сохранению прямолинейной формы вала и этим отличается от самоцентрирования диска при высоких скоростях вращения, когда происходит центрирование массы диска при соответственно изогнутом вале.
Один из вариантов автоматического балансировщика состоит в том, что схема вал-диск усложняется двумя маятниками, которые могут свободно вращаться на валу. Ограничимся рассмотрением стационарных режимов вращения и для упрощения будем пренебрегать силами веса и неупругими сопротивлениями.
Пусть - точка, лежащая на
прямой, проходящей через центры подшипников; - центр сечения вала; - центр тяжести диска;
-центры масс маятников; 
- длина маятников; 
- эксцентриситет
(рис.82).
а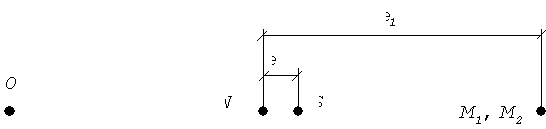 
б 
в 
г 
д 
Рис.82
При
отсутствии маятников возможны две схемы взаимного расположения точек 
и (рис.82). В каждой
схеме центробежная сила и сила упругости вала действуют по одной прямой,
поэтому, добавляя маятники, можно предположить, что в любой из этих схем оси
обоих маятников имеют направление той же прямой.
Это приводит
к четырем вариантам расположения характерных точек. Варианты а и б (рис.82)
соответствуют схеме, данной на рис.81,а, когда центр тяжести диска лежит дальше от оси
вращения, чем центр сечения вала ; эти варианты различаются между собой относительным
положением точек 
и 
.
Варианты в и
г соответствуют схеме, данной на рис.82,б, когда центр тяжести диска S лежит ближе к оси вращения, чем центр сечения вала .
Эти четыре
варианта исчерпывают все возможные принципиально различные случаи взаимного
расположения точек 
, если все они лежат на одной прямой. Но возможен еще пятый
вариант (рис.82,д), соответствующий полной балансировке вала, когда центр
сечения вала совпадает с центром
вращения системы . В этом варианте силы упругости отсутствуют, так как вал не
изогнут, а центробежная сила диска уравновешена центробежными силами маятников.
При этом оси маятников образуют некоторый угол 
, соответствующий данному эксцентриситету диска.
Хотя
равновесие возможно в каждом из перечисленных вариантов стационарного режима,
но не все эти режимы будут устойчивыми. Теоретический анализ и эксперименты
показывают, что при устойчивостью обладает
только пятый вариант. Поэтому в закритической области такие маятники служат
автоматическими балансировщиками и удерживают ось вала от изгиба; если в
процессе вращения эксцентриситет увеличивается, т.е. точка на рис.82,д смещается
вправо, то маятники сходятся ближе и угол уменьшается ровно
настолько, насколько это необходимо для уравновешивания возросшей центробежной
силы диска.
В
докритической области, при 
, устойчивым оказывается режим а (рис.82), в котором маятники увеличивают прогиб вала и поэтому
приносят только вред. Поэтому в реальных системах принимают меры по
«выключению» маятников в докритической области.
В
конструкциях стиральных машин маятниками служат кольца, заключенные в кожух.
При 
центробежные силы,
действующие на кольца, малы, кольца лежат на дне кожуха, и балансировщик
«выключен». При центробежные силы
оказываются достаточными, чтобы кольца «всплыли» и произошло включение
балансировщика.
В некоторых конструкциях шлифовальных станков маятниками служат шары, заключенные в кожух.
10.3.
Критические состояния ротора вертолета
Формулы,
приведенные при рассмотрении вала с одним диском, нельзя использовать, если с
вращающимся диском связаны массы, обладающие некоторой подвижностью по
отношению к диску; в частности, в (359)
для критической угловой скорости нельзя подставлять вместо суммарную массу диска
вместе с присоединенными массами.
К схемам
этого типа относится, например, горизонтальный вертолетный ротор, состоящий из
втулки и лопастей, которые связаны с втулкой вертикальными шарнирами. На рис.83
показан трехлопастный ротор, причем - центр втулки, 
- центры вертикальных
шарниров. Предположим, что вертолет стоит на земле, а центр втулки будем считать упруго
закрепленным в горизонтальной плоскости; эта упругость создается всей
конструкцией вертолета.
Схематизируем
массовые свойства системы и будем считать, что лопасти полностью уравновешены,
причем масса 
каждой лопасти
сосредоточена на расстоянии 
от центра
соответствующего вертикального шарнира. Допустим также, что втулка уравновешена
не полностью и ее центр тяжести 
находится на
расстоянии е от центра втулки и на биссектрисе угла 
(рис.83,а).
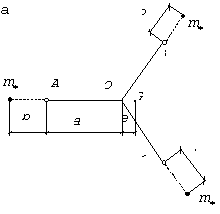
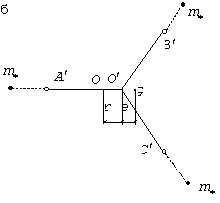
Рис.83
Вследствие неуравновешенности
системы при вращении ротора возникает центробежная сила, которая вызовет
дополнительное упругое смещение центра втулки
(рис.83,б), где 
- смещенное положение
центра втулки; - ее центр тяжести; 
- центры вертикальных
шарниров. Этими буквами обозначено некоторое мгновенное положение ротора; с
течением времени точки ,, описывают окружности с
центром в точке , которая определяет ось вращения системы. Оси лопастей,
подвешенных в шарнирах 
и 
, уже не будут располагаться на прямых 
и 
, так как центробежные силы лопастей должны проходить через
центр вращения . Угол, который ось каждой из этих лопастей составляет с
прямой 
, будет несколько меньше 
; обозначим его как 
(рис.83,в).
Из
треугольника 
имеем:
отсюда,
вследствие малости 
:
Центробежные силы лопастей:
- лопасть 
;
- лопасть 
;
- лопасть 
.
Схема
центробежных сил показана на рис.83,г. Кроме центробежных сил лопастей, сюда
включена центробежная сила втулки ,
где - масса втулки.
Сумма всех
этих сил направлена вдоль прямой 
и равна:
Так как
то окончательно получим:
(361)
Смещение равно частному от деления силы 
на коэффициент жесткости упругой системы. После подстановки в это
отношение выражения (361) получим простое уравнение для определения ,
решение которого дает:
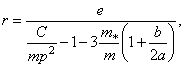
и тогда критическая скорость составляет:
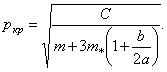(362)
Дополнительным
слагаемым 
выражено влияние подвижности лопастей
относительно втулки; если рассматривать систему без вертикальных шарниров
(жесткий ротор), то
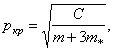
что
значительно больше, чем 
.
Формула (362)
справедлива для любого числа лопастей 
с заменой числа 3 на число 
.
10.4.
Колебания лопаток турбомашин
Колебания лопаток турбомашин возникают вследствие неравномерного по окружности потока рабочей среды, а также в связи с возмущениями, вносимыми в поток лопатками направляющего аппарата. Задачей проектировщика является расчет собственной частоты колебаний лопатки и выбор такой ее конструкции, которая позволяет исключить возможность резонанса.
Лопатка газовой турбины или компрессора представляет собой стержень переменного сечения, заделанный одним концом. Ось лопатки обычно является слабо изогнутой пространственной кривой, но при расчете частоты колебаний можно с достаточной точностью считать, что ось лопатки прямолинейна и перпендикулярна оси вращения ротора.
Трудности расчета частоты собственных колебаний лопаток связаны с необходимостью учитывать влияние центробежных сил и с тем, что лопатка представляет собой естественно закрученный стержень, главные оси различных поперечных сечений которого не параллельны друг другу.
Закрученная
лопатка в процессе колебаний испытывает косой изгиб. Установим соотношение
между изгибающими моментами и кривизнами для этого случая. Поперечное сечение
лопатки, расположенное на расстоянии от оси вращения,
отнесем к осям 
направленным
соответственно параллельно оси вращения и по касательной к окружности (рис.84,а).
Главные оси
сечения и 
составляют некоторый
угол с осями и 
. Площадь сечения, его моменты инерции и угол являются функциями
радиуса или расстояния 
данного сечения от
корневого сечения лопатки. Положительные направления изгибающих моментов,
приложенных к внутренней части лопатки, свяжем с направлениями 
правилом правого
винта.
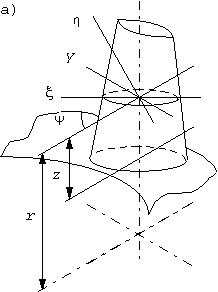
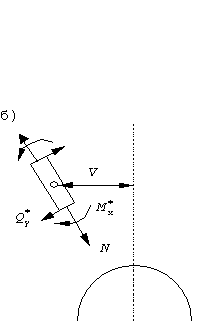
Рис.84
Изгибающие
моменты относительно осей связаны соотношениями:
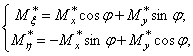(363)
где знак «
» означает текущее значение переменной, а его отсутствие -
соответствующее амплитудное значение.
Кривизны,
отнесенные к главным осям сечения 
, выражаются через изгибающие моменты относительно этих осей
формулами:
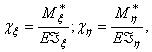(364)
а кривизны,
отнесенные к осям и -
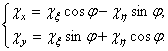(365)
После подстановки (363) в (364), а затем - в (365), получим:
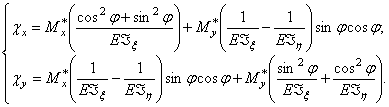(366)
В этих равенствах кривизны можно заменить их приближенными выражениями:
(367)
где 
- смещения центра
тяжести лопатки в осевом и окружном направлениях.
На основе
принципа Даламбера для составления уравнений движения рассмотрим динамическое
равновесие элемента 
лопатки в плоскости,
перпендикулярной оси вращения. На концах элемента возникают внутренние силы -
продольная 
,
поперечная 
и изгибающий момент 
(рис.84,б). Кроме
того, к элементу приложена центробежная сила, имеющая вертикальную 
и горизонтальную 
проекции (рис.84,в), а
также сила инерции в относительном движении, равная 
.
Проектируя силы на вертикаль, получим:
(368)
Сумма проекций на горизонталь дает уравнение:
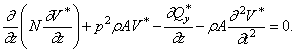(369)
И третье уравнение, сумма моментов, дает:
(370)
Уравнение (368) позволяет вычислить продольную силу в сечении:
(371)
которую,
следовательно, можно считать заданной. В формуле (371) 
- длина лопатки.
Уравнения
движения элемента в плоскости 
(рис.85,а) имеют вид:
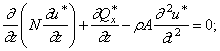
Выражения для смещений и силовых факторов, соответствующие свободным колебаниям лопатки, представим в форме:
Тогда получим систему обыкновенных дифференциальных уравнений, состоящую из уравнений динамического равновесия:
(372)
и уравнений упругости:
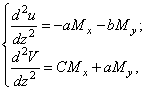
где
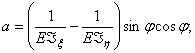
Рис.85
Полученные уравнения можно записать в матричной форме:
(373)
где 
- матрица-столбец из
восьми элементов:
- матрица переменных
коэффициентов размером 
, ненулевые элементы которой:
Для определения
частот собственных колебаний из уравнения (373) может быть использован метод
начальных параметров. С этой целью конструируются четыре линейно независимых
решения уравнения (373), удовлетворяющие граничным условиям в сечении 
. Например, для заделанного сечения такие решения при могут иметь значения:
Численно
интегрируя уравнение (373) при этих начальных условиях и при фиксированном
значении частоты 
, находят значения 
при 
.
Общее решение
в сечении представляет собой
линейную комбинацию частных решений:
Граничные
условия при (
) приводят к системе однородных уравнений относительно 
. Если при расчете принято истинное значение собственной
частоты , то определитель этой системы равен нулю. Это условие
позволяет, повторяя расчет при различных значениях , определить собственные частоты колебаний. Для применяемых в
практике профилей лопаток момент инерции поперечных сечений относительно одной
из главных осей 
существенно больше,
чем момент инерции относительно другой оси 
. В этом наиболее важном с практической точки зрения случае
расчет можно существенно упростить, пренебрегая изгибом относительно оси . При этом существенными становятся только изгибающий момент 
и соответствующая
кривизна 
.
Для решения упрощенных уравнений эффективным является метод последовательных приближений.
Можно также
использовать метод Рэлея в варианте Граммеля. Зададимся изменением кривизны по длине лопатки,
тогда интегрированием уравнений
можно найти соответствующие смещения:
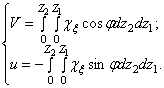(374)
Потенциальная энергия деформации определяется по формуле:
(375)
Обобщенная масса:
(376)
Для учета центробежных сил нужно дополнительно вычислить их потенциал. Предположим, что в процессе колебаний точки оси лопатки движутся по нормали к недеформированной оси. Тогда дополнительная деформация удлинения лопатки в связи с изгибом составляет:
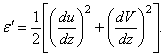
Работа
начального усилия 
растяжения лопатки на
этой деформации равна
При
перемещении в плоскости вращения точки лопатки удаляются от оси вращения на
расстояние 
(рис.85,б), что
приводит к уменьшению потенциала массы лопатки в поле центробежных сил на
величину
Таким образом, общее увеличение энергии составляет:
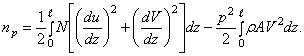
Так как
продольная сила в лопатке пропорциональна 
, то окончательно получим:
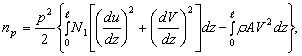
где 
- усилие в лопатке при
.
После
определения 
и 
частота собственных
колебаний лопатки вычисляется по формуле Рэлея:
10.5.
Понятие о динамическом гасителе колебаний
В динамическом гасителе для гашения колебаний используется явление антирезонанса.
Рассмотрим
простейшую систему с одной степенью свободы, совершающую вынужденные гармонические
колебания с частотой 
. Если дополнительно присоединить к системе гаситель,
состоящий из диска с моментом инерции 
и вала жесткостью 
(рис.86), причем,
настроить гаситель так, чтобы его собственная частота при закрепленном диске равнялась :
,
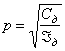то частота станет для
получившейся двухмассовой системы антирезонансной и движение основного диска прекратится.
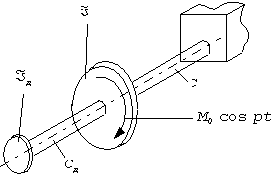
Рис.86.
Амплитуда 
колебаний диска
гасителя может быть найдена из условия, что крутящий момент на валу гасителя
уравновешивает возмущающий момент 
:
Проследим
поведение системы с динамическим гасителем при изменении частоты возбуждения . Если гаситель отклонить, то амплитуда 
колебаний основной
системы будет определяться по формуле:
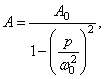
где
.
Уравнения движения системы при включенном гасителе:
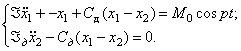(377)
Углы
поворотов основного диска и гасителя 
и 
зададим в форме:
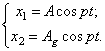
Углы
поворотов основного диска и гасителя и и их вторые
производные в (377) и решая полученную систему уравнений, получим:
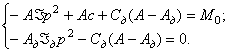
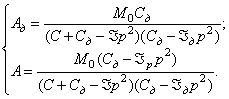(378)
При нулевой амплитуде основного диска, т.е. при отсутствии колебаний:
или
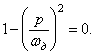
Таким
образом, благодаря установке гасителя устраняются колебания основной системы
при частоте 
, но сохраняются резонансные колебания при 
и 
, т.е. динамический гаситель колебаний эффективен только при
постоянной частоте возбуждения.
Устранить
резонансные колебания при частотах 
и 
оказывается возможным,
если ввести в конструкцию динамического гасителя трение.
В двигателях
внутреннего сгорания используются также динамические гасители, частота
настройки которых меняется автоматически с изменением частоты возбуждения.
Принцип работы этих гасителей основан на том, что собственная частота маятника
в поле центробежных сил пропорциональна скорости вращения. Поэтому, подвесив
маятник к диску, закрепленному на коленчатом валу двигателя и выбрав
соответствующим образом радиус качения, можно добиться того, чтобы собственная
частота колебаний маятника была в 
раз больше, чем
угловая скорость диска. Такой виброгаситель устраняет крутильные колебания,
вызываемые второй, третьей, ..., -ной гармониками возмущающих моментов.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Строительная механика Теория машин и механизмов
