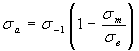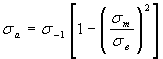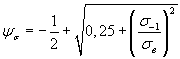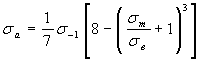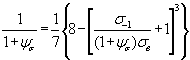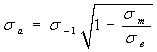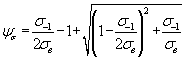Главная

Раздел 11. Усталость материалов и конструкций

Предисловие

Первые наблюдения усталостного разрушения относятся к концу XVIII века, когда у длительно эксплуатируемых дилижансов в Англии и почтовых карет во Франции неожиданно для инженерного мира стали хрупко ломаться оси, изготовленные из кованого железа, обладающего высокой пластичностью. Специалисты того времени объясняли это явление перерождением материала за счет его усталости в процессе длительной эксплуатации под действием переменных напряжений, возникающих из-за неровностей дороги. С тех пор термин "Усталость материалов", хотя не отражающий полностью сложные процессы, протекающих в металле под воздействием напряжений, переменных во времени, нашёл высокое распространение в инженерных методах расчёта надёжности элементов конструкций.

Первые систематические экспериментальные исследования сопротивления усталостному разрушению стальных образцов при действии переменных нагрузок были проведены немецким ученым А. Велером, который опубликовал результаты исследований в виде итоговых таблиц в 1870 г. Графическое представление этих результатов в виде кривых усталости впервые было осуществлено Л. Шпангенбергом в 1875 г., хотя в мировой практике эти кривые связываются только с именем А. Велера.

Усталость материалов и в настоящее время является одной из основных причин отказа деталей машин и элементов конструкции, подверженных действию напряжений, циклически изменяющихся во времени. В связи с этим для повышения ресурса и надежности подобных конструкций важное значение приобретают вопросы выбора материала, обоснования режимов технологии производства полуфабрикатов и деталей и организации контроля технологического процесса, обеспечивающие стабильное и высокое сопротивление элементов конструкций усталостному разрушению.

Решения проблемы повышения ресурса и надёжности машин обусловливает разработку и внедрение вероятностных методов расчёта на прочность при переменных напряжениях, учитывающих случайный характер действующих нагрузок и вариацию характеристик сопротивления усталости материалов и деталей.

Характеристики сопротивления усталостному разрушению материала и изделий определяются в результате испытаний на усталость образцов, моделей, натурных деталей и конструкций в целом, что требует больших материальных затрат и весьма длительного времени, которого, как правило, не хватает конструктору на стадии проектирования и доводки конструкции. В связи с этим ученые многих стран ведут поиски расчётных (косвенных) методов оценки характеристик сопротивления усталостному разрушению и методов ускоренных и форсированных испытаний на усталость.

1. Характеристики сопротивления усталости конструкционных материалов, используемые в расчётах на прочность при многоцикловом нагружении

В данном разделе рассматриваются основные характеристики сопротивления усталости материалов и деталей, термины, определения и обозначения, применяемые в науке и технике, в соответствии с ГОСТ 23207—78.

1.1. Циклы напряжений. Характеристики цикла.

Совокупность последовательных значений напряжений за один период их изменения при регулярном нагружении (рис.1.1) называется циклом напряжений.

Характеристики цикла напряжений.

Частота циклов f — отношение числа циклов напряжений к интервалу времени их действия.

Период цикла Т – продолжительность одного цикла напряжений, T=1/f (рис.1.1.)

Максимальное напряжение цикла — наибольшее по алгебраическому значению напряжение цикла (рис. 1.1., рис. 1.2.)

Минимальное напряжение цикла — наименьшее по алгебраическому значению напряжение цикла (рис.1.1, 1.2).

Среднее напряжение цикла — постоянная (положительная или отрицательная) составляющая цикла напряжений (рис.1.1, 1.2), равная алгебраической полусумме максимального и минимального напряжения цикла,

;

Амплитуда напряжений цикла — наибольшее числовое положительное значение переменной составляющей цикла напряжений (рис.1.1., рис.1.2.), равная алгебраической полуразности максимального и минимального напряжения цикла

;

Размах напряжений цикла — алгебраическая разность максимального и минимального напряжения цикла, , .

Коэффициент асимметрии цикла напряжений , отношение минимального напряжения цикла к максимальному,

;

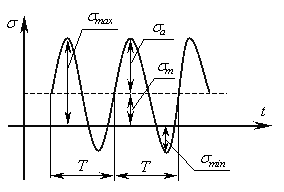
Рис. 1.1. Циклы напряжений

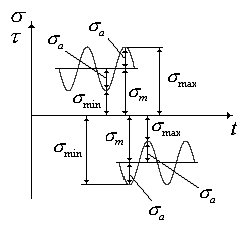
Рис. 1.2. Параметры циклов нагружения в области растяжения и сжатия

1.2. Разновидности циклов напряжений

Симметричный цикл напряжений (рис.1.3, г) – цикл, у которого максимальное и минимальное напряжения равны по абсолютному значению, но противоположны по знаку, ; ; ; .

Асимметричный цикл напряжений (рис.1.3, а, б, в, д, е, ж) – цикл, у которого максимальные и минимальные напряжения имеют разные абсолютные значения ; .

Знакопеременный цикл напряжений (рис. 1.3, в, г, д) – цикл напряжений, изменяющихся по значению и по знаку, ; ; ; .

Знакопостоянный цикл напряжений (рис.1.3, а, б, е, ж) – цикл напряжений, изменяющихся только по абсолютному значению.

Отнулевой цикл напряжений (рис.1.3, б, е) – знакопостоянный цикл напряжений, изменяющихся от нуля до максимума (; ) или от нуля до минимума (;)

Подобные циклы напряжений — циклы, у которых коэффициенты асимметрии одинаковы.

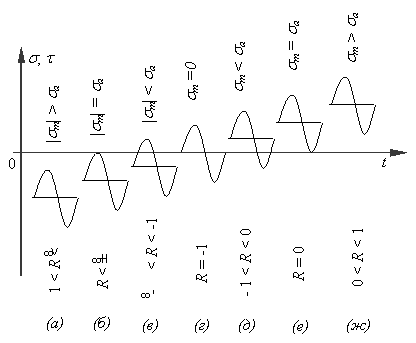
Рис. 1.3. Разновидности циклов напряжений и соответствующие им значения коэффициентов асимметрии

1.3. Характеристики сопротивления усталости при регулярном нагружении

Циклическая долговечность (N) – число циклов напряжений, выдержанных нагруженным объектом до образования усталостной трещины определенной протяженности или до усталостного разрушения, при неизменных характеристиках цикла напряжений.

Малоцикловая усталость – усталость материала, при которой усталостное повреждение или разрушение происходит при упруго-пластическом деформировании. Условно принимают, что при N < 50000 циклов имеет место малоцикловая усталость.

Многоцикловая усталость – усталость материала, при котором усталостное повреждение или разрушение происходит, в основном, при упругом деформировании. Условно принимают, что при N > 50000 циклов имеет место многоцикловая усталость.

База испытаний – предварительно задаваемое наибольшее число циклов при испытании на усталость.

Кривая усталости , или , – график, характеризующий зависимость между максимальными напряжениями или амплитудами цикла и циклической долговечностью одинаковых образцов, построенный по параметру среднего напряжения цикла или по параметру коэффициента асимметрии цикла (рис.1.4, а, б). Участок I на рис.1.4соответствует малоцикловой усталости, а участки II и III – многоцикловой. Участок III для углеродистых и низколегированных сталей обычно имеет горизонтальный линейный характер. Для высоколегированных сталей и сплавов на магниевой, алюминиевой и титановой основах этот участок представляет собой кривую, стремящуюся к асимптоте при .

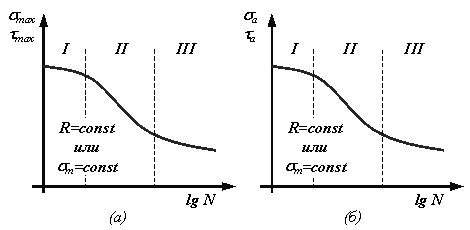
Рис. 1.4. Варианты представления кривой усталости.

1.4. Разновидности уравнений кривых усталости

1.4.1. Уравнения кривых усталости

Для описания кривых усталости сталей используются:

Уравнение Велера (1870 г.)

или ; (1.1)

Уравнение Басквина (1910 г.)

или ; (1.2)

Уравнение Штромейера (1914 г.)

или; (1.3)

Уравнение Пальмгрена (1924 г.)

или

; (1.4)

Уравнение Вейбулла (1949 г.)

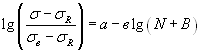
или

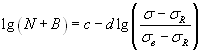. (1.5)

Уравнения (1.1) и (1.2) описывают только II участок кривых усталости, уравнение (1.3) – II и III участки, уравнения (1.4) и (1.5) охватывают все три участка кривых усталости.

Применительно к легким сплавам (магниевым, алюминиевым и титановым) для указанных участков кривых усталости могут использоваться уравнения (1.3), (1.4) и (1.5).

Однако, как показали специальные исследования [1,2], более адекватно экспериментальным данным соответствует уравнение Степнова М.Н. (1970 г.).

(1.6)

Параметр B в уравнениях (1.4) и (1.5), а также параметр N₁, в уравнении (1.6), определяют положение кривой усталости только в малоцикловой области (участок I на рис. 1.4). Поэтому при описании кривой многоцикловой усталости без ущерба для точности принимают B=0 и N₁=0.

1.4.2. Схематизированные кривые усталости для сталей

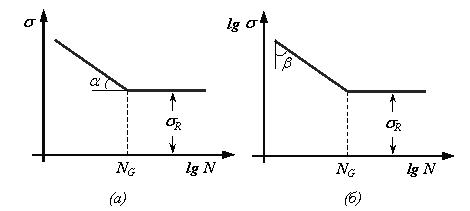
Рис. 1.5. Схематизированные кривые усталости для сталей.

Левая ветвь кривой усталости на рис. 1.5, а соответствует уравнению Велера (1.1), где , а на рис. 1.5, б – уравнению Басквина (1.2), которое чаще в технической и учебной литературе представляют в виде

, где . (1.7)

Абсцисса точки перелома схематизированной кривой усталости N_G (рис. 1.5, а, б) обычно принимает значения в диапазоне циклов.

Предел ограниченной выносливости , - максимальное по абсолютному значению напряжение цикла, соответствующее задаваемой циклической долговечности N. Пределы ограниченной выносливости выражаются в номинальных напряжениях.

Предел выносливости , - максимальное по абсолютному значению напряжение цикла, при котором не происходит усталостное разрушение до ; выражается в номинальных напряжениях.

Предел выносливости при симметричном цикле , - определяется по результатам испытаний на усталость при симметричном цикле напряжений, для которого ; .

Предел выносливости при отнулевом цикле напряжений , - определяется по результатам испытаний на усталость при отнулевом цикле напряжений, для которого ; .

Предельные напряжения цикла , , , - максимальное и минимальное напряжения цикла, соответствующие пределу выносливости, ; .

Предельная амплитуда и предельное среднее напряжение, соответствующие пределу выносливости,

; ;

; .

Диаграмма предельных напряжений цикла – график, характеризующий зависимость между значениями предельных напряжений и значениями средних напряжений цикла для заданной долговечности (рис.1.6).

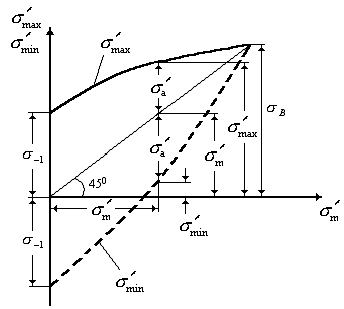
Рис. 1.6. Диаграмма предельных напряжений цикла: сплошная линия — , штриховая —

Диаграмма предельных амплитуд цикла – график, характеризующий зависимость между значениями предельных амплитуд и значениями средних напряжений цикла для заданной долговечности (рис.1.7.)

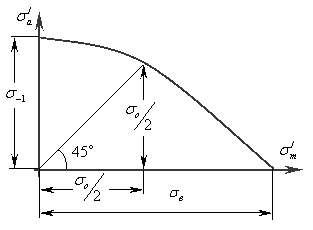
Рис. 1.7. Диаграмма предельных амплитуд цикла.

В качестве уравнения диаграммы предельных амплитуд на практике используются:

Уравнение Гудмана

, (1.8)

Уравнение Гербера

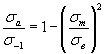, (1.9)

Уравнение И.А.Одинга

(1.10)

Уравнение Петерсона

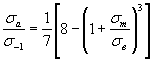(1.11)

Уравнение И.А. Биргера

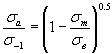(1.12)

Уравнение М.Н. Степнова

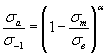(1.13)

и другие.

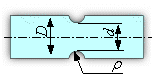
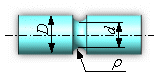
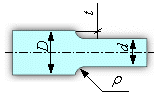
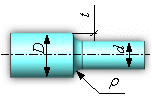
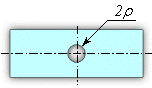
Концентрация напряжений — повышение напряжений в местах изменения формы или нарушения сплошности материала (рис.1.8).

Надрез – резкие изменения размеров и формы объекта, вызывающее концентрацию напряжений (рис.1.8).

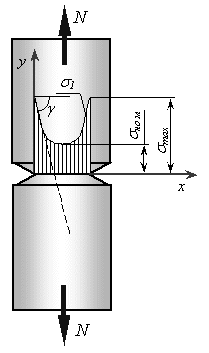
Рис. 1.8. Эпюра номинальных и первого главного напряжения в зоне надреза.

Номинальное напряжение — напряжение, вычисляемое по формулам сопротивления материалов без учёта концентрации напряжений, остаточных напряжений и упругопластического перераспределения напряжений в процессе деформирования,

, , .

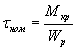Теоретический коэффициент концентрации напряжений – характеристика концентрации напряжений при упругом деформировании ,

, .

Градиент первого главного напряжения — или (см. рис.1.8.)

Относительный градиент первого главного напряжения — .

Градиент касательного напряжения — скорость изменения касательного напряжения по направлению Х.

Относительный градиент касательного напряжения — .

Эффективный коэффициент концентрации напряжений , — отношение предела выносливости образцов без концентрации напряжений к пределу выносливости образцов с концентрацией напряжений, имеющих такие же абсолютные размеры сечения, как и гладкие образцы,

, при .

Пределы выносливости с концентрацией напряжений и выражаются в номинальных напряжениях.

Коэффициент чувствительности к концентрации напряжений , - величина, определяемая по формуле

или .

Коэффициент влияния абсолютных размеров поперечного сечения , — отношение предела выносливости гладких образцов диаметром d к пределу выносливости гладких лабораторных образцов d₀=7,5-10 мм,

; .

Коэффициент влияния шероховатости поверхности K_F — отношение предела выносливости образцов с данной шероховатостью поверхности к пределу выносливости образцов с поверхностью не грубее R_a=0.32,

; .

Коэффициент влияния поверхностного упрочнения , — отношение предела выносливости упрочненных образцов к пределу выносливости не упрочненных образцов,

; .

Коэффициент снижения предела выносливости K — отношение предела выносливости стандартных гладких образцов к пределу выносливости объекта при симметричном цикле напряжений,

; .

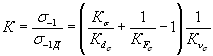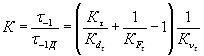Коэффициент чувствительности к асимметрии цикла напряжений , — величина, определяемая по формулам

, .

2. Расчетные методы оценки характеристик сопротивления усталости материалов и конструкций (детерминированный подход)

2.1. Расчет предела выносливости материала при симметричном цикле напряжений

Длительность и высокая стоимость испытаний на усталость побудили появление косвенных методов оценки предела выносливости материала, базирующихся на результатах статических испытаний материала и применении корреляционного и регрессионного анализа опытных данных.

Как показали результаты многочисленных исследований отечественных и зарубежных ученых, предел выносливости имеет тесную корреляционную связь с пределом прочности (временным сопротивлением) при статическом нагружении. На начальной стадии изучения сопротивления усталости материала предел выносливости сталей выражали как некую долю предела прочности,

(2.1)

В капитальной монографии английского ученого Р.Хейвуда [3], например, принято, что отношение предела выносливости при симметричном растяжении-сжатии к пределу прочности сталей, равно K=0,5. С учетом этого отношения им были разработаны методы оценки прочности деталей и элементов конструкций, обеспечивающие для того времени достаточную надежность инженерных решений.

Среди отечественных ученых наиболее серьезные исследования связей между усталостными и статическими характеристиками сталей выполнил С.Л.Жуков, который в послевоенные годы (1945 - 1947 гг.) опубликовал серию статей, посвященную этой проблеме.

В качестве основного уравнения линии регрессии С.Л.Жуковым и целым рядом других последователей использовалось линейное уравнение вида

(2.2)

В ряде работ использовались линейные уравнения двумерной и многомерной регрессии, связывающие предел выносливости сталей с характеристиками прочности и пластичности.

Ниже для примера приведены наиболее характерные уравнения, предложенные рядом авторов, для оценки предела выносливости при симметричном изгибе с вращением,

(С.Л.Жуков)

(С.Л.Жуков)

(С.Л.Жуков)

(С.Л.Жуков)

(С.Л.Жуков)

(В.М.Гребеник)

(С.Л.Жуков)

(М.П.Марковец)

(В.М.Гребеник)

Все эти уравнения, а также уравнения (2.1) и (2.2), имеют два серьезных недостатка. Во-первых, в работах указанных и других авторов рассматривается лишь линейный характер связи между механическими характеристиками и без какого-либо обоснования игнорируется нелинейная зависимость, которая, как показывает регрессионный анализ [4], более адекватна опытным данным. Во-вторых, из-за относительно ограниченного объема статистического материала в этих работах недостаточно внимания уделено надежному обоснованию средней квадратической ошибки оценивания предела выносливости и её зависимости от уровня прочности материала, что не позволяет оценивать нижние (гарантированные) значения материалов различной прочности.

2.1.1. Оценка предела выносливости при переменном изгибе

Автором совместно с сотрудниками и студентами кафедры [5,6] на основании большого статистического материала рассмотрена и показана возможность достаточно надежной косвенной оценки предела выносливости при симметричном изгибе образцов из алюминиевых и титановых деформируемых сплавов, углеродистых и легированных сталей на основании значений предела прочности при статическом растяжении; рассмотрена точность подобной оценки и даны рекомендации по определению нижних (гарантированных) значений предела выносливости.

Анализу были подвергнуты 187 вариантов алюминиевых деформируемых сплавов в различном состоянии, 152 варианта титановых сплавов, 317 вариантов углеродистых и 393 варианта легированных сталей в различных состояниях (варианты режимов термической обработки, виды полуфабрикатов и т.д.). Предел прочности алюминиевых сплавов менялся в диапазоне от 100 до 650 МПа, титановых сплавов – от 350 до 1475 МПа, углеродистых сталей от 300 до 1700 МПа, легированных – от 450 до 2150 МПа. Анализу подверглись результаты испытаний, опубликованные в отечественной и зарубежной литературе.

В качестве уравнений линии регрессии рассматривались линейное (2.2) и степенное

, (2.3)

которое путем логарифмирования приводится к линейному

(2.4)

где , , , .

Предел выносливости для алюминиевых и титановых сплавов соответствует базе 10⁷циклов.

Уравнения (2.3) и (2.4) в отличие от линейного уравнения (2.2) удовлетворяют граничным условиям (при ; ).

Коэффициент корреляции r между пределом выносливости при симметричном изгибе и пределом прочности при растяжении в случае линейного соотношения (2.2) для всех рассматриваемых материалов находится в пределах 0.87...0.92 и отличается от выборочного значения корреляционного отношения [4] не более, чем на 2..3 величины среднего квадратического отклонения коэффициента корреляции S_r, что не дает достаточных оснований для отклонения линейного уровня (2.2), хотя оно и не удовлетворяет граничным условиям (при ; ). Значение оценок параметров уравнения (2.2), средней квадратической ошибки предела выносливости и относительной погрешности на разных участках линии регрессии приведены в таблице 2.1. Относительная средняя квадратическая ошибка в средней части линии регрессии определяется величиной ; на границах линии регрессии ошибка находится с учетом её зависимости от уровня прочности материала.

Таблица 2.1 Параметры уравнения (2.2) и значения ошибки оценивания предела выносливости на разных участках линии регрессии

Материал	Уравнение линии регрессии*	, МПа	Относительная средняя квадратическая ошибка оценивания предела выносливости на разных участках линии регрессии.
			Начало	Середина	Конец
Алюминиевые сплавы		15	0,15	0,10	0,07
Титановые сплавы		65	0,26	0,17	0,11
Углеродистые стали		53	0,20	0,15	0,08
Легированные стали		53	0,18	0,11	0,07
*Здесь и далее напряжения и имеют размерность МПа.

Как показывают эксперименты и теоретические расчеты, средняя квадратическая ошибка в определении путем непосредственных испытаний на усталость 8...10 образцов на кривую усталости, как того требует ГОСТ, составляет для алюминиевых сплавов 5...7 %, для сталей 5...10 % и титановых сплавов 7...15%. Поэтому погрешность косвенной оценки предела выносливости материалов средней и высокой прочности (середина и конец линии регрессии), превышающую в 1.5...2 раза ошибку при усталостных испытаниях, следует считать удовлетворительной. Однако, для материалов низкой прочности (начало линии регрессии) это различие достигает 2...3 раз.

При объединении двух классов сталей в единую совокупность (n = 668, = 290...2130 МПа, r = 0.906, =53.8 МПа) уравнение линии регрессии запишется как

, (2.5)

причем, относительная ошибка оценки предела выносливости на всём протяжении линии регрессии возрастает на 1.2%, что позволяет использовать уравнение (2.5) как для углеродистых сталей, так и для легированных.

При использовании в качестве уравнения линии регрессии выражения (2.4) коэффициент корреляции для рассматриваемых материалов увеличивается до 0.91...0.95, причем, расхождение с эмпирическим корреляционным отношением не превышает одной величины S_r, что говорит о практически полной адекватности линии регрессии экспериментальным данным [4].

Статистический анализ показал, что дисперсия экспериментальных значений вокруг линии регрессии (2.4) практически не зависит от уровня .

Эта закономерность равносильна постоянству средней квадратической ошибки оценивания предела выносливости по уравнению (2.3) для материалов малой, средней и высокой прочности.

Объединение углеродистых и легированных сталей в один статистический коллектив и в этом случае привел к увеличению погрешности оценивания предела выносливости лишь на несколько процентов, хотя параметры уравнения (2.4) статистически значимо отличаются друг от друга. Это говорит о высокой чувствительности применяемого метода статистического анализа.

Уравнения (2.3) для указанных материалов с численными значениями параметров и величиной относительной средней квадратической ошибки оценивания предела выносливости при переменном изгибе приведены ниже:

а) алюминиевые сплавы

, (2.6)

б) титановые сплавы

, (2.7)

в) углеродистые стали

, (2.8)

г) легированные стали

, (2.9)

д) объединенная совокупность сталей

, (2.10)

Таким образом, нелинейное уравнение (2.3) имеет следующие преимущества перед линейным уравнением (2.2):

а) выполняются граничные условия;

б) увеличивается коэффициент корреляции r;

в) снижается ошибка оценивания предела выносливости для материалов средней и низкой прочности;

Поэтому для косвенной оценки предела выносливости при переменном изгибе для указанной группы конструкционных материалов следует пользоваться уравнениями (2.6)-(2.10).

Для дальнейшего повышения надежности получаемых косвенным образом характеристик сопротивления усталости целесообразно для практических целей использовать нижнюю (гарантированную) границу предела выносливости, которая определяется из выражения

, (2.11)

здесь - нижняя (гарантированная) граница значения медианы предела выносливости, которая с вероятностью Р не ниже действительного значения медианы предела выносливости для рассматриваемого материала; - оценка медианы предела выносливости по уравнениям (2.6)-(2.10); - относительная средняя квадратическая ошибка оценивания медианы предела выносливости по уравнениям (2.6)-(2.10); z_p — квантиль уровня Р нормального распределения (для Р=0.90, 0.95 и 0.99 значения z_p = 1.28, 1.64 и 2.33 соответственно [4]).

На рисунке 2.1-2.3 показаны зависимости оценки медианы предела выносливости при переменном изгибе и нижних гарантированных значений для вероятностей 0,90 и 0,99 от значений при статическом растяжении образцов из деформируемых алюминиевых и титановых сплавов, а также из углеродистых и легированных сталей.

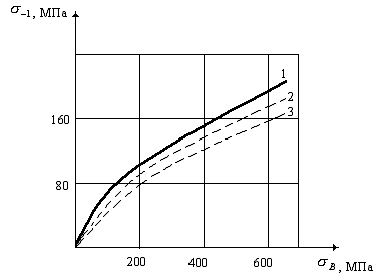
Рис.2.1. Зависимость медианы предела выносливости при переменном изгибе на базе 10⁷ циклов от предела прочности при статическом растяжении для деформируемых алюминиевых сплавов: 1- оценка медианы предела выносливости; 2,3- нижняя граница медианы для вероятностей Р=0,9 и 0,99 соответственно.

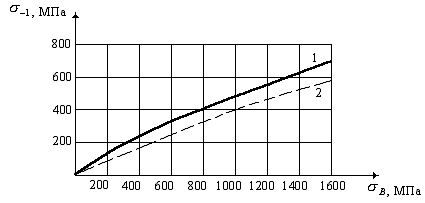
Рис.2.2. Зависимость медианы предела выносливости при переменном изгибе на базе 10⁷ циклов от предела прочности при статическом растяжении для деформируемых титановых сплавов: 1- оценка медианы предела выносливости; 2- нижняя граница медианы для вероятностей Р=0.90

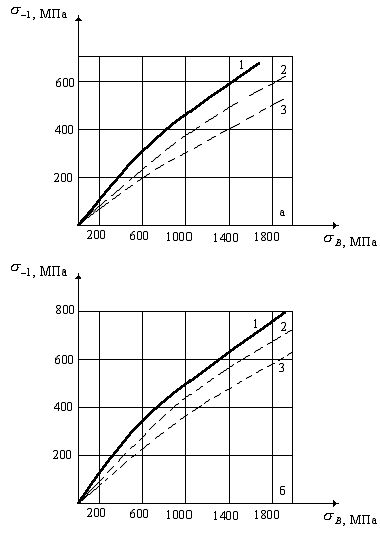
Рис.2.3. Зависимость медианы предела выносливости при переменном изгибе от предела прочности при статическом растяжении для углеродистых (а) и легированных (б) сталей: 1-3 – то же, что на рис.2.1.

В соответствии с ГОСТ 25.504-82 оценка предела выносливости при переменном изгибе может производиться также по следующим нелинейным зависимостям:

а) стали (углеродистые и легированные)

(2.12)

б) высокопрочный чугун (В. Ч.)

(2.13)

в) ковкий чугун (К. Ч.)

(2.14)

г) серый чугун (С. Ч.)

(2.15)

2.1.2. Оценка предела выносливости при переменном растяжении-сжатии

В связи со сравнительно ограниченным по объему статическим материалом, касающегося испытаний на усталость при симметричном растяжении-сжатии, не представляется возможность надежного обоснования параметров уравнения линии регрессии (2.3) для оценки предела выносливости, как это было рассмотрено в предыдущем параграфе применительно к переменному изгибу образцов.

В этом разделе рассмотрен другой подход к вопросу оценки предела выносливости рассматриваемых конструкционных материалов и вычисление средней квадратической ошибки его расчета.

На основании существующих литературных данных произведены оценки среднего значения и среднего квадратического отклонения отношения для каждого класса рассмотренных конструкционных материалов по формулам

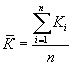и 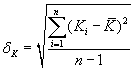(2.16)

Здесь и- пределы выносливости соответственно при растяжении-сжатии и переменном изгибе; n – число вариантов сплавов и их состояний для рассматриваемого класса материалов.

Предел выносливости при растяжении-сжатии и средняя квадратическая ошибка оценивания с учетом (2.16) вычисляется по формулам

(2.17)

и

(2.18)

С учетом уравнений (2.6)...(2.10), (2.13)...(2.15) получим

а) для углеродистых сталей сплавов (=0,919)

; ; (2.19)

б) для легированных сталей сплавов (=0,914)

; ; (2.20)

в) для общей совокупностей сталей сплавов (=0,916)

; ; (2.21)

г) для деформируемых алюминиевых сплавов (=0,954)

; ; (2.22)

д) для деформированных титановых сплавов (=0,829)

; ; (2.23)

е) для чугунов в соответствии с ГОСТ 25.504-82

=0,65 (С. Ч.), =0,60 (К. Ч.), =0,70 (В. Ч.)

и пределы выносливости при растяжении-сжатии оцениваются с учетом формулы (2.17) и уравнений (2.13) – (2.15).

2.1.3. Оценка предела выносливости при переменном кручении

Как установлено экспериментально, для сталей и деформируемых алюминиевых сплавов = 0.60, для деформируемых титановых сплавов = 0.514, =0.80, 0.85 и 0.75 для С.Ч., К.Ч. и В.Ч. соответственно, где σ_-1 и τ_-1 — пределы выносливости при переменном изгибе и переменном кручении.

С учетом уравнений (2.6)-(2.10) и (2.13)-(2.15) предел выносливости при переменном кручении для указанных материалов вычисляется по формулам:

для деформируемых алюминиевых сплавов (N_б=10⁷ циклов)

(2.24)

для деформируемых титановых сплавов (N_б=10⁷ циклов)

(2.25)

для углеродистых сталей

(2.26)

для легированных сталей

(2.27)

для общей совокупности сталей

(2.28)

В случае чугунов предел выносливости при кручении оценивается с учетом приведенных выше значений отношения и уравнений (2.13)-(2.15).

2.2. Расчет характеристик сопротивления усталости конструкционных материалов при асимметричном цикле напряжений

При расчетах на усталость деталей методом, предложенным С.В. Серенсеном и Р.С. Кинасошвили [7,8], для вычисления коэффициента запаса прочности оценку предельной амплитуды цикла напряжений лабораторных гладких образцов производят с применением коэффициента чувствительности к асимметрии цикла напряжений и (см. п. 1.4.29) на основании выражений

(2.29)

и

. (2.30)

В этом случае предел выносливости или предельное максимальное напряжение определяется по формулам

(2.31)

и

. (2.32)

Коэффициент чувствительности к асимметрии цикла напряжений определяют экспериментально, либо берут из справочной литературы. Применение формул (2.29), (2.30) равносильно использованию в качестве уравнения диаграммы предельных амплитуд линейной зависимости, что противоречит опытным данным.

В авиационной практике для оценки характеристик сопротивления усталости при асимметричном цикле напряжений широко используются уравнения И.А.Одинга (1.10). Как показал дальнейший расчет, коэффициент чувствительности к асимметрии цикла при использовании уравнения (1.10) для всех конструкционных материалов принимает единое значение =0.41, что находится в противоречии с экспериментальными данными.

2.2.1. Расчет предельной амплитуды цикла по методу М.Н. Степнова

В основу метода расчетной оценки предельной амплитуды цикла напряжений положена, выдвинутая М.Н. Степновым [1], гипотеза о том, что изменение предельной амплитуды из-за влияния среднего напряжения цикла, эквивалентно изменению предела выносливости материала при симметричном нагружении за счет снижения его предела прочности на величину, равную среднему напряжению цикла.

Правомерность выдвинутой гипотезы вытекает из результатов экспериментов, представленных на рис. 2.4, где совмещены две зависимости в координатах и (светлые точки) и в координатах и (темные точки). Темные точки, соответствующие асимметричному нагружению, более или менее равномерно перемешиваются со светлыми точками, соответствующими результатам экспериментов при симметричном растяжении-сжатии, и описываются единым уравнением . Если принять в качестве указанной функции при симметричном нагружении уравнение (2.3), то для асимметричного нагружения получим зависимость,

, (2.33)

которая и позволяет оценивать предельные амплитуды цикла напряжений.

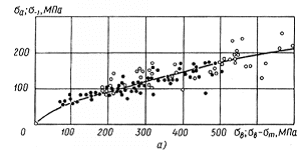
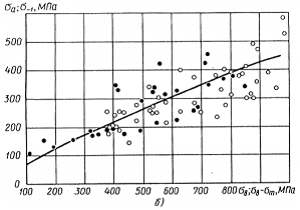
Рис.2.4 Зависимости предела выносливости от предела прочности (светлые точки) и предельной амплитуды от разности предела прочности и среднего напряжения цикла (темные точки) для алюминиевых сплавов (база N=10⁷ циклов) (а) и сталей (б); сплошная линии – расчет по уравнению (2.33); точки – экспериментальные значения.

Для конкретных конструкционных материалов и видов напряжения уравнения типа (2.33) приведены в таблице 2.2

Таблица 2.2 Уравнения для расчета предельных амплитуд цикла напряжений для конструкционных материалов

№ п/п	Материал	Вид деформаций
		Асимметричный изгиб	Асимметричное растяжение- сжатие
1	Деформируемые алюминиевые сплавы*
2	Деформируемые титановые сплавы*
3	Углеродистые стали
4	Легированные стали
5	Объединенная совокупность сталей
Примечание: * для базы Nб = 10^7циклов

Как показал статистический анализ расчетных и экспериментальных значений предельных амплитуд цикла напряжений, использование уравнений, приведенных в таблице 2.2, повышает относительную ошибку оценивания по сравнению с формулами (2.6) - (2.10) и (2.19) - (2.23) ещё лишь на 2.3%, что дополнительно подчеркивает правомочность использованной гипотезы.

2.2.2. Расчет предельной амплитуды цикла по методу Р. Хейвуда

Метод Р. Хейвуда [3] разработан для оценки предельной амплитуды цикла напряжений деформируемых алюминиевых сплавов и сталей применительно к переменному растяжению-сжатию.

Для сталей предельная амплитуда на базе N_б=10⁷циклов определяется по уравнению

, (2.34)

где

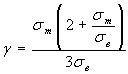
Для деформируемых алюминиевых сплавов предельная амплитуда цикла для той же базы рассчитывается по формуле

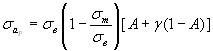, (2.35)

где

,

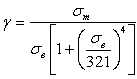Сходимость экспериментальных и расчетных значений в соответствии с формулами (2.34) и (2.35) удовлетворительная, но по сравнению с формулами, приведенными в таблице (2.2), относительная погрешность повышается на 4.5%.

2.3. Расчетный метод построения кривых усталости при симметричном цикле напряжений

Р. Хейвуд [3] предложил метод построения кривых усталости при растяжении-сжатии образцов, в соответствии с которым ординаты точек кривой для сталей подсчитываются по формуле

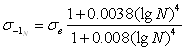(2.36)

и для деформируемых алюминиевых сплавов

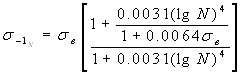, (2.37)

где - ордината кривой усталости для долговечности N.

Относительная средняя квадратическая ошибка оценивания величины по формуле (2.37) составляет =14% при систематической (относительной средней алгебраической) ошибке =1%.

2.3.1. Метод М.Н. Степнова - С.П. Евстратовой

Метод М.Н. Степнова – С.П.Евстратовой построения кривой усталости для деформируемых алюминиевых сплавов базируется на понятии обобщенной кривой усталости

Если для указанных сплавов ординаты точек кривой усталости представить в виде отношения , где и — пределы ограниченной выносливости соответственно для заданной долговечности N и долговечности базы N=10⁷ циклов, то для всех деформируемых алюминиевых сплавов кривые усталости практически совпадают друг с другом и описываются единым уравнением, называемым уравнением обобщенной кривой усталости [1],

(2.38)

С учетом (2.6) и (2.22) уравнение (2.38) принимает вид

(2.39)

для переменного изгиба и

(2.40)

для переменного растяжения-сжатия.

Сходимость расчетных значений с использованием формул (2.39) и (2.40) с экспериментальными вполне удовлетворительная (относительная средняя квадратическая ошибка составляет 10% при отсутствии систематической ошибки).

Как показали дальнейшие исследования [2], метод М.Н.Степнова - С.П.Евстратовой применим и для деформируемых титановых сплавов.

Для обоснования уравнения обобщенной кривой усталости титановых сплавов [2] из ряда литературных источников, включающих и исследования автора, были отобраны построенные экспериментальным путем кривые усталости при переменном изгибе, протяженностью от 10⁵ до 10⁸ циклов нагружений (анализировалось 92 значения предела ограниченной выносливости для различных баз). Предел прочности рассматриваемых сплавов находился в диапазоне от 700 до 1300 МПа.

Предварительный графический анализ показал, что применительно к титановым сплавам также, как и для алюминиевых, имеет место обобщенная кривая усталости, построенная в координатах [1].

Использование статистического анализа вышеупомянутых экспериментальных результатов показало, что из всех известных уравнений кривых усталости наиболее адекватны опытным данным с достаточно высоким уровнем значимости являются следующие уравнения:

ранее обоснованное для алюминиевых сплавов [1] в виде

(2.41)

и уравнение Штромейера (1.3)

, (2.42)

где и — соответственно пределы ограниченной выносливости для произвольной базы N и базы N_б=10⁷ циклов, a, b, c, d, , — параметры уравнений.

С помощью регрессионного анализа [4] была произведена оценка указанных параметров. Окончательно уравнения кривых усталости при переменном изгибе для титановых сплавов представляются в виде

(2.43)

и

(2.44)

Как показывают расчеты, расхождение в ординатах кривых усталости, построенных по этим уравнениям, в диапазоне долговечности 10⁵...10⁹ циклов не превышает 1%, а при расхождение между ними чуть выше 2%. Таким образом, в статистическом плане эти уравнения равноценны. На практике же следует отдать предпочтение первому уравнению, обеспечивающему более надежные результаты при прогнозировании сопротивления усталости на больших долговечностях.

Относительное среднее квадратическое отклонение расчетных значений по уравнениям (2.43) и (2.44) от экспериментальных данных при долговечности 10⁵ циклов составляет около 6%, и для долговечностей в диапазоне 10⁶...10⁸ циклов – не превышает 3%.

Уравнения (2.43) и (2.44) содержат единственный неизвестный параметр, поэтому они позволяют построить кривые усталости по результатам испытаний лишь на одном уровне амплитуды цикла напряжений, что обеспечит значительное сокращение временных и материальных затрат на проведения испытаний.

Установленные ранее [6] корреляционное соотношение (2.7) между пределом ограниченной выносливости при переменном изгибе для базы 10⁷ циклов и пределом статической прочности титановых сплавов

,

открывает возможность построения кривых усталости расчетным методом на основании данных о статической прочности сплавов.

Применительно к симметричному циклу переменного изгиба уравнения кривых усталости (2.43) и (2.44) с учетом (2.7) примут вид

(2.45)

(2.46)

Относительное среднее квадратическое отклонение ординат экспериментальной кривой усталости от расчетных значений по уравнениям (2.45) и (2.46) составляет около 15%. Следует иметь в виду, что средняя квадратическая погрешность экспериментального определения медианы предела выносливости или предельной амплитуды цикла напряжений при испытании на усталость 8...10 образцов на одну кривую, как того требует существующий стандарт, соизмерима с величиной коэффициента вариации предела выносливости, который для титановых сплавов составляет =7..15%.

Таким образом, предложенный метод расчетного построения кривых усталости для титановых сплавов по своей точности соизмерим с экспериментальным методом.

Проведенный анализ результатов отечественных и зарубежных исследований показал, что отношение пределов ограниченной выносливости при симметричном растяжении-сжатии и переменном изгибе образцов из титановых сплавов слабо зависит от базы испытаний и составляет в среднем 0.829 [6]. В связи с этим и в соответствии с формулой (2.7) оценка предела выносливости при симметричном растяжении-сжатии лабораторных образцов при отсутствии концентрации напряжений для титановых сплавов на базе 10⁷ циклов может быть произведена по формуле (2.23).

Уравнения обобщенной кривой усталости (2.43) и (2.44) и соотношение (2.33) позволяют строить кривую усталости для симметричного растяжения-сжатия образцов из титановых сплавов расчетным способом по уравнениям

(2.47)

и

. (2.48)

Относительное среднее квадратическое отклонение расчетных значений предельных амплитуд напряжений по уравнениям (2.47) и (2.48) и экспериментальных результатов с учетом наблюдаемой дисперсии отношения составляет 17%, что лишь на 2...5% превышает относительную среднюю квадратическую ошибку экспериментального определения предела выносливости при переменном растяжении-сжатии путем испытания на усталость серии из 8...10 образцов.

2.3.2. Построение схематизированных кривых усталости для сталей

Горизонтальный участок схематизированных кривых усталости, представленных на рис.1.5, проводят от точки с абсциссой N_G, значение которой принимают равной 2·10⁶ циклов [8]. Ординату этой точки при симметричном цикле нагружения вычисляют по уравнениям (2.8)...(2.10), (2.19)...(2.21). При асимметричном цикле напряжений предел выносливости вычисляют по формуле

(2.49)

где — предельная амплитуда цикла напряжений, определяемая по соответствующей формуле, представленной в таблице 2.2.

Левая ветвь кривой усталости, представленной на рис.1.5а, проводится под углом к горизонтальному участку, тангенс которого вычисляют по формуле В.М.Гребеника [9]

. (2.50)

Левую ветвь кривой усталости в двойных логарифмических координатах (рис.1.5б) проводят под углом к вертикали, тангенс которого вычисляют по формуле В.П. Когаева [8]

. (2.51)

2.4. Расчетный метод построения кривых усталости при асимметричном цикле напряжений

2.4.1. Метод Р. Хейвуда

Р. Хейвуд [3] разработал метод расчета ординат кривых усталости для выбранных значений долговечности при асимметричном растяжении-сжатии. Применительно к сталям предельная амплитуда цикла рассчитывается по формуле

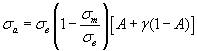, (2.52)

где

,

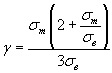Сходимость с опытными данными, как отмечает автор [3], удовлетворительная.

Для деформируемых алюминиевых сплавов построение кривых при асимметричном растяжении-сжатии производят на основании уравнения

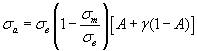, (2.53)

где

, .

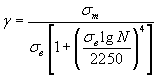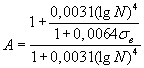Экспериментальная проверка уравнения (2.53) производилась путем сопоставления расчетных значений предельных амплитуд для долговечностей 10⁵, 10⁶, 10⁷ и 10⁸ циклов и опытных данных, полученных отечественными и зарубежными исследователями, применительно к 93 кривым усталости 26 вариантов деформируемых алюминиевых сплавов и их состояний. Сходимость с экспериментальными данными оказалась удовлетворительной. Относительная средняя квадратическая ошибка составила 16% и относительная средняя алгебраическая (систематическая) ошибка — 6%.

Следует отметить, что в отечественной практике уравнение Р. Хейвуда (2.53) не получило применения из-за содержащейся в нем опечатки в русском варианте монографии [3].

При необходимости построения кривой усталости при асимметричном изгибе следует воспользоваться отношением, значения которого приведены в п. 2.1.2.

2.4.2. Метод Степнова М.Н.

Метод М.Н. Степнова [1] расчетного построения кривых усталости при асимметричном цикле нагружения для деформируемых алюминиевых и титановых сплавов базируется на уравнениях обобщенной кривой усталости (2.38).(2.40), (2.43), (2.45), (2.47) и методике оценки предельной амплитуды цикла напряжений.

Применительно к алюминиевым сплавам уравнения кривых усталости при асимметричных изгибе и растяжении-сжатии соответственно записываются в виде в виде

(2.54)

(2.55)

Экспериментальная проверка этих уравнений производилась путем сопоставления расчетных значений предельных амплитуд для долговечностей 10⁵, 10⁶, 10⁷ и 10⁸ циклов и опытных данных, упомянутых в разделе 2.4.1.

Статистический анализ показал, что уравнения (2.54) и (2.55) при отсутствии систематической ошибки обеспечивают оценку предельной амплитуды цикла для указанных выше долговечностей с относительной средней квадратической ошибкой, равной =12%, что лишь на 5-7% превышает погрешность определения предельной амплитуды цикла путем непосредственных испытаний на усталость серии из 8...10 образцов, как того требует действующий стандарт.

Для титановых сплавов уравнения кривых усталости при асимметричных изгибе и растяжении-сжатии соответственно имеют вид

(2.56)

и

(2.57)

Имеющиеся экспериментальные результаты удовлетворительно согласуются с выше приведенными уравнениями; относительное среднее квадратическое отклонение (ошибка) расчетных от экспериментальных значений предельных амплитуд не превышает 16...18%, что определяется в основном погрешностью эксперимента при испытании партии 8...10 образцов на одну кривую усталости.

Для расчетного построения кривых усталости при асимметричном нагружении, ординаты которых представлены в максимальных напряжениям, следует к левой и правой частям уравнений (2.52...2.57) прибавить значения среднего напряжения цикла .

Например, для случая уравнения (2.57) ординаты соответствующей кривой усталости должны подсчитываться по формуле

Аналогично можно поступить с уравнениями (2.52...2.56).

2.5. Построение диаграммы предельных амплитуд при отсутствии концентрации напряжений

Экспериментальный метод построения указанных диаграмм весьма трудоемкий, так как требует испытания на усталость нескольких серий образцов при различной степени асимметрии цикла с целью определения соответствующих значений предельных амплитуд. Следует иметь в виду, что погрешность экспериментального определения медианы предела выносливости или предельной амплитуды цикла при испытании на усталость серии из 8...10 образцов соизмерима с величиной коэффициента вариации предела выносливости, который для деформируемых алюминиевых сплавов составляет = 5...7%, титановых сплавов = 7...15%, сталей — = 5...10%.

Уравнения диаграммы предельных амплитуд цикла напряжений Гудмана (1.8) и Геребера (1.9), как показывает анализ экспериментальных данных, ограничивают снизу и сверху соответственно примерно 95% всех экспериментальных значений предельной амплитуды цикла напряжений и, следовательно, не могут быть использованы для расчета предельных амплитуд и оценки прочности элементов конструкции.

2.5.1. Метод Степнова М.Н.

Расчетный метод М.Н. Степнова базируется на уравнении диаграммы предельных амплитуд цикла напряжений в виде

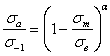, (2.58)

которое получается путем деления уравнения (2.33) на уравнение (2.3) [1], где - предел выносливости при симметричном цикле напряжения для выбранной базы (долговечности). Значения параметра для основных классов конструкционных материалов приведены в таблице (2.3).

Формулу для расчета предельной амплитуды цикла напряжений применительно к сталям, а также деформируемым алюминиевым и титановым сплавам для базы N = 10⁷ циклов, получают путем подстановки в уравнение (2.58) расчетного значения предела выносливости при симметричном цикле нагружения по формуле (2.3)

(2.59)

Значения параметров (2.59) приведены в таблице 2.3.

Таблица 2.3 Значения параметров С и уравнений (2.58) и (2.59) для разных классов конструкционных материалов

Материал		С		Источник
		при переменном изгибе	при переменном растяжении-сжатии
Углеродистая сталь	0,850	1,23	1,13	[5]
Легированная сталь	0,777	2,21	2,02	[5]
Общая совокупность сталей	0,820	1,75	1,60	[5]
Титановые сплавы*	0,831	1,55	1,29	[6]
Алюминиевые сплавы*	0,630	3,49	3,33	[1,5,10,11,12]
Примечание: * для базы Nб = 10^7 циклов.

Применительно к деформируемым алюминиевым и титановым сплавам расчет предельной амплитуды цикла напряжений для произвольной базы осуществляется соответственно по формулам (2.54), (2.55) и (2.56), (2.57).

Структура уравнения (2.58) предполагает независимость диаграммы предельных амплитуд, построенной в относительных координатах, от базы испытаний.

Для проверки этого положения был проведен однофакторный дисперсионный анализ [4] экспериментальных данных, который показал, что диаграмма предельных амплитуд в указанных координатах является единой для всех рассмотренных баз испытаний (N=10⁵...10⁸ циклов). Этот вывод иллюстрирует рисунок 2.5 применительно к сплаву 7075-Т6 с = 576 МПа [13].

Как видно из графика все экспериментальные точки ложатся на общую кривую, построенную по уравнению (2.58).

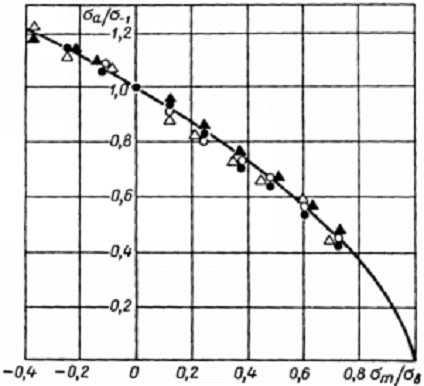
Рис.2.5. Диаграмма предельных амплитуд для сплава 7075-Т6 в относительных координатах: , , — экспериментальные точки соответственно для баз испытания 10⁵, 10⁶, 10⁷ и 10⁸ циклов; сплошная линия – расчет по уравнению (2.58).

Правомочность высказанной ранее гипотезы о характере влияния среднего напряжения на величину предельной амплитуды цикла, т. е. адекватность уравнения (2.33) опытным данным, была дополнительно проверенна на основании 93 кривых усталости 26 вариантов деформируемых алюминиевых сплавов и их состояний. Для этой цели уравнение (2.58) путем логарифмического преобразования было приведено к линейному виду.

(2.60)

где

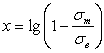, и .

Регрессионный анализ упомянутых экспериментальных данных [4] показал адекватность уравнения (2.60) экспериментальным данным для всех рассмотренных баз испытаний (N_б = 10⁵, 10⁶, 10⁷ и 10⁸ циклов) с высоким уровнем значимости, а оценка параметра , произведенная в соответствии с методом наименьших квадратов по формуле

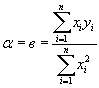, (2.61)

оказалась в среднем равной для всех упомянутых баз испытаний с колебаниями не превышающими одного среднего квадратического отклонения значения параметра.

Это обстоятельство дополнительно подтверждает независимость диаграммы предельных амплитуд, построенной в относительных координатах, от базы испытаний (см. рис.2.5).

Уравнения (2.58) и (2.59), как показал анализ опытных данных для алюминиевых сплавов, удовлетворительно согласуется с результатами экспериментов и отрицательных средних напряжениях, если , где - предел текучести материала.

2.5.2. Метод Р. Хейвуда

Расчетный метод Р. Хейвуда базируется на использовании уравнений (2.52) и (2.53).

На рис. 2.6 приведены для сравнения диаграммы предельных амплитуд рассчитанные методами М.Н. Степнова и Р. Хейвуда, и экспериментальные значения для сплава 7075-Т6 [13].

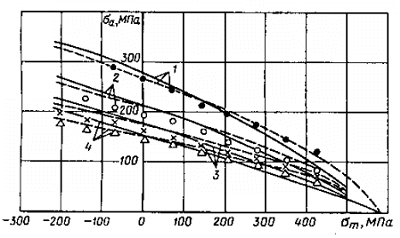
Рис.2.6. Диаграммы предельных амплитуд для сплава 7075-Т6:
штриховая линия – расчет по уравнению (2.55), сплошная – по уравнению (2.53); точки – эксперимент;
база испытаний N=10⁵ (1), 10⁶ (2), 10⁷ (3) и 10⁸ (4) циклов.

Как следует из приведенного графика оба метода удовлетворительно описывают диаграмму предельных амплитуд цикла напряжений как в области положительных значений , так и в области отрицательных , хотя, как было установлено, метод М.Н. Степнова с большей точностью позволяет оценивать предельную амплитуду цикла напряжений, чем метод Р. Хейвуда.

Из других известных уравнений диаграммы предельных амплитуд удовлетворительное соответствие с опытными данными имеет уравнение И.А. Биргера (1.12) и уравнение Петерсона (1.11), хотя их точность заметно ниже уравнения М.Н. Степнова (2.59). Уравнения Гудмана, Гербера и И.А. Одинга и др. из-за больших погрешностей не могут быть рекомендованы для построения диаграммы предельных амплитуд цикла напряжений.

2.6. Построение диаграммы пределов выносливости предельных максимальных напряжений цикла

Рассмотренная ранее методика построения расчетным способом диаграммы предельных амплитуд цикла напряжений позволяет построить диаграмму предельных максимальных напряжений (пределов выносливости) и предельных минимальных напряжений (рис. 1.6). С этой целью для определения предела выносливости при асимметричном цикле изменения напряжений к вычисленной по формулам (2.52), (2.53), (2.59) величине следует прибавить значение среднего напряжения цикла, т. е.

(2.62)

Для определения предельного минимального напряжения следует из среднего напряжения цикла вычесть значение амплитуды, найденное по формуле (2.52), (2.53) и (2.59), т. е.

(2.63)

С учетом (2.52).(2.59) упомянутые диаграммы можно строить для различных баз испытаний, как это показано на рис. 2.7.

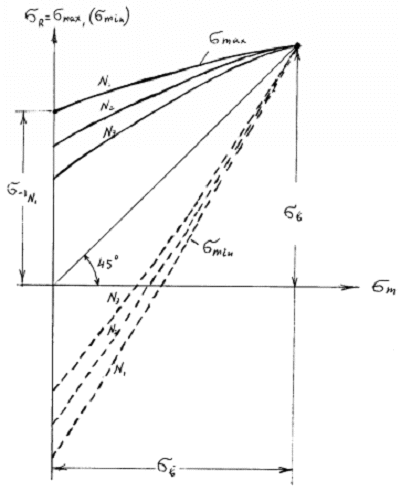
Рис. 2.7. Диаграммы предельных максимальных и минимальных напряжений цикла: N₁< N₂< N₃;

сплошная линия — , штриховая линия — .

2.7. Расчетный метод определения коэффициента чувствительности материала к асимметрии цикла напряжений

При схематизации предельной нагруженности и в расчетах на прочность деталей, работающих в условиях действия переменных напряжений, в качестве характеристики материала широко используются коэффициенты и , учитывающие чувствительность материала к асимметрии цикла напряжений, определяемые по формулам

, , (2.64)

где и — пределы выносливости материала соответственно при симметричном и отнулевом циклах напряжений. В соответствии с ГОСТом 25.504-82 [14] принимают .

В настоящее время используются три метода определения коэффициента чувствительности к асимметрии цикла напряжений — экспериментальный, эмпирический и расчетный (теоретический).

2.7.1. Экспериментальный метод

Экспериментальный метод, как это вытекает из формулы (2.64), требует испытаний на усталость двух партий образцов при симметричном и отнулевом циклах с целью определения соответствующих пределов выносливости материала.

Следует иметь в виду, что погрешность экспериментального определения медианы предела выносливости путем испытания на усталость партии из 8...10 образцов, как того требует существующий стандарт, соизмерима с величиной коэффициента вариации предела выносливости [4], который для конструкционных деформируемых алюминиевых сплавов, как уже отличалось ранее, составляет = 5...7%, для титановых сплавов = 7...15%, для углеродистых и легированных сталей = 5...10%.

Как показали расчеты в соответствии с формулой для дисперсии функции случайных аргументов [28], коэффициент вариации величины в 6-7 раз превышает величину коэффициента вариации пределов выносливости. Это означает, что при испытании на усталость двух партий по 8...10 образцов с целью экспериментального определения величины , относительная средняя квадратическая ошибка составит для алюминиевых сплавов 30...50%, для титановых 40...100%, для сталей 30...70%, что не может быть приемлемо для практических целей.

Увеличение же объемов партий образцов для испытания на усталость до 30...40 штук приводит к весьма большим материальным и временным затратам.

2.7.2. Эмпирический метод

Эмпирический метод оценки коэффициента чувствительности материала к асимметрии цикла напряжений заключается в статистическом обобщении накопленных в отечественной и зарубежной практике результатов экспериментов по отдельным близким группам конструкционных материалов.

Так, например, в ныне действующем стандарте [14] и работе [8] рекомендуется формула для расчетов применительно к сталям

, (2.65)

где в МПа.

Следует отметить, что формула (2.65) противоречит опытным данным и, как будет показано ниже (формула (2.76)), теоретическим расчетам. Корреляционный и регрессионный анализ опытных данных отечественных и зарубежных исследователей (рис. 2.8) указывает на убывание величины коэффициента чувствительности асимметрии цикла с ростом статической прочности сталей. Коэффициент корреляции между наблюдаемыми в экспериментах значениями и оказался отрицательным и равным r = -0.28, что говорит о снижении чувствительности асимметрии цикла напряжений с ростом статической прочности сталей [15].

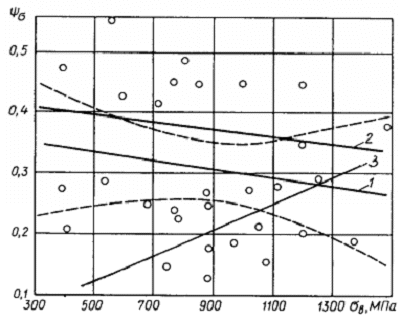
Рис. 2.8. Зависимости коэффициента сталей от предела прочности:
1- линия регрессии [уравнение (2.66)]; 2- расчет по формуле (2.76); 3- расчет по формуле (2.65); o — экспериментальные значения; штриховые линии – границы 95% -ой доверительной области.

Уравнение эмпирической линии регрессии для сталей по результатам, представленным на рис. 2.8, имеет вид

. (2.66)

Статистическому анализу было подвержено 30 вариантов марок сталей и их состояний.

Большой разброс экспериментальных значений , связанный с упомянутым ранее малым объемом испытаний на каждую кривую усталости (8...10 образцов), при сравнительно ограниченным объеме выборке (30 вариантов сталей) определили высокую меру индивидуального рассеяния вокруг линии регрессии = 0.11 и весьма широкую 95%-ную доверительную область линии регрессии.

В связи с этим формулой (2.66) можно пользоваться только для приблизительной оценки . Для повышения точности этой формулы следует привлечь к статистическому анализу дополнительные экспериментальные данные, доведя объем выборки до 100...150 вариантов сталей и их состояний, что в настоящее время представляется трудно выполнимой задачей.

Экспериментальные данные для 30 вариантов алюминиевых сплавов, представлены на рис. 2.9. Коэффициент корреляции между коэффициентов чувствительности к асимметрии для базы N = 10⁷ циклов и пределом прочности тоже оказался отрицательным и равным r = - 0.23. Индивидуальная мера рассеяния вокруг линии регрессии достигает = 0,14, что соответствует средней квадратической ошибке оценки по корреляционному уравнению (40...60%).

Однако, осреднение по ряду баз испытания позволяет снизить указанную ошибку в 2 раза. В этом случаи, корреляционное уравнение имеет вид [1, 10, 11]

, (2.67)

где N — база испытания.

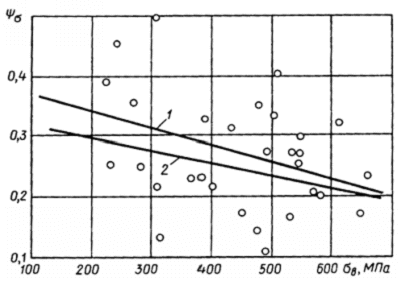
Рис.2.9. Зависимости коэффициента алюминиевых сплавов от предела прочности: 1 - линия регрессии [уравнение (2.67)]; 2 - расчет по формуле (2.78); o - экспериментальные значения

Таким образом, экспериментальный и эмпирический подходы к оценке величины коэффициента чувствительности материала к асимметрии нагружения не являются надежными.

2.7.3. Теоретический метод

Для теоретического метода определения коэффициента чувствительности требуется выбрать наиболее достоверное уравнение диаграммы предельных амплитуд и корреляционное соотношение между пределом выносливости при симметричном цикле и пределом прочности материала [15].

Связь между пределом выносливости и пределом прочности металлических конструкционных материалов, как уже частично отмечалось ранее, обычно представляют одним из следующих трех уравнений ( в МПа):

, (2.68)

, (2.69)

. (2.70)

Параметры уравнений (2.68) и (2.69), найденные путем статистического анализа больших по объему совокупностей (нескольких сотен на вариант) экспериментальных данных представлены в табл. 2.4. Уравнение (2.70) рекомендуется стандартом [14] только для сталей.

Все уравнения (2.68)...(2.70) для соответствующих групп материалов приводят к близким результатам, однако предпочтение следует отдавать формуле (2.69), так как она не противоречит, в отличие от (2.68), граничным условиям и, как показал анализ, обеспечивает наибольшую точность оценки предела выносливости [1, 5, 6, 12].

Таблица 2.4. Значения параметров уравнений (2.68) и (2.69) для базы N_б = 10⁷ циклов при переменном растяжении-сжатии

Материал	a	b	с		Источник
Углеродистые стали	33,5	0,379	1,13	0,850	[5]
Легированные стали	105	0,329	2,02	0,777	[5]
Общая совокупность сталей	69,2	0,354	1,60	0,820	[5]
Титановые сплавы	56,5	0,347	1,29	0,831	[6]
Алюминиевые сплавы	76,6	0,175	3,33	0,630	[1, 5, 10, 11, 12]

Как уже отмечалось ранее, существует достаточно широкий круг уравнений для диаграмм предельных амплитуд цикла напряжений, в соответствии с которыми получаются различные формулы для теоретического расчета коэффициента чувствительности материала к асимметрии нагружения .

Эти формулы, наряду с широко используемыми в расчетной практике уравнениями диаграмм предельных амплитуд цикла напряжений, приведены в таблице 2.5.

Совместные решения уравнений (2.71).(2.74) с одним из уравнений (2.68)...(2.70) открывает возможность теоретической (расчетной) оценки коэффициента чувствительности материала к асимметрии цикла напряжений [15].

Таблица 2.5. Формулы для вычисления на базе различных уравнений диаграмм предельных амплитуд

Уравнение диаграммы предельных амплитуд (автор)	Номер формулы	Формула для вычисления коэффициента	Номер формулы
(Гудман)	1.8		2.71
(Гербер)	1.9		2.72
(Петерсон)	1.11		2.73
(Биргер)	1.12		2.74

В качестве примере на рис. 2.10 для сталей показана зависимость коэффициента , рассчитанного по формулам (2.71)...(2.74) с использованием уравнения (2.69), от уровня статической прочности.

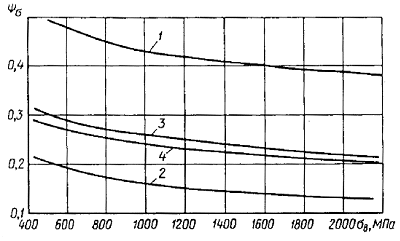
Рис. 2.10. Расчетные значения коэффициента для сталей: 1, 2, 3, 4 – расчет по уравнениям (2.71), (2.72), (2.73), (2.74) соответственно

Для легированных и углеродистых сталей приведенные графики практически совпадают, поэтому здесь и далее для этих групп сталей будут приводиться осредненные данные.

Как видно из рис.2.10, величина коэффициента чувствительности монотонно убывает с увеличением статической прочности сталей для всех видов используемых уравнений диаграммы предельных амплитуд (1.8), (1.9), (1.11), (1.12), что соответствует экспериментальным данным, представленным на рис.2.8, и противоречит уравнению (2.65), рекомендуемому стандартом [14]. Причем, как и следовало ожидать, выбор уравнения, связывающего предел выносливости материала с пределом прочности, не имеет сколько-нибудь значимого влияния. Для иллюстрации этого на рис. 2.11 приведены зависимости величины коэффициента чувствительности от предела прочности сталей, причем для расчета использовались все уравнения (2.68)...(2.70).

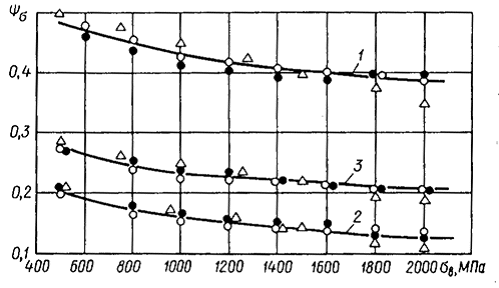
Рис.2.11. Расчетные значения коэффициента для сталей: 1,2,3– расчет по уравнениям (2.71), (2.72), (2.74) соответственно, , , — расчет на базе формул (2.68), (2.69), (2.70) соответственно

Аналогичные результаты имеют место для титановых и алюминиевых сплавов.

Обращает на себя внимание весьма сильная зависимость значений коэффициента , получаемых расчетным путем, от вида выбранного уравнения диаграммы предельных амплитуд цикла напряжений. Причем, при использовании уравнений Гудмана и Гербера отношение расчетных значений , получаемых по формулам (2.71) и (2.72), достигает 2,5...3 раз для сталей и титановых сплавов и 3...3,5 раз для алюминиевых сплавов.

Таким образом, точность теоретической оценки коэффициента чувствительности к асимметрии цикла нагружения зависит от степени обоснованности соответствующего уравнения для диаграммы предельных амплитуд. Следует заметить, что уравнения (1.8), (1.9), (1.11), (1.12) не имеют строгого теоретического обоснования, а были получены путем анализа граничных условий и чисто умозрительных построений.

Известное уравнение И. А. Одинга

(1.10)

приводит к значению = 0,41 для всех групп конструкционных металлических материалов, что также не согласуется с опытными данными.

Ранее было дано обоснование уравнения диаграммы предельных амплитуд цикла напряжений в виде

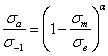(2.58)

или с учетом (2.3)

(2.59)

Значения параметров этих уравнений приведены в таблице 2.3.

Использование формул (2.3), (2.58) и (2.59) для теоретического определения коэффициента чувствительности к асимметрии цикла нагружения приводит к уравнениям, решение которого возможно методом последовательных приближений,

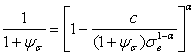, (2.75)

где c и — параметры материала, представленные в табл. 2.3.

На рис. 2.12 показана зависимость теоретической оценки коэффициента чувствительности (2.75) от статической прочности исследуемых материалов. Представленные графики указывают на возможность в первом приближении их аппроксимации прямыми линиями, что значительно упрощает теоретический расчет величины , который проводится соответственно для сталей, титановых и алюминиевых сплавов по формулам

, (2.76)

, (2.77)

, (2.78)

где - предел прочности в МПа.

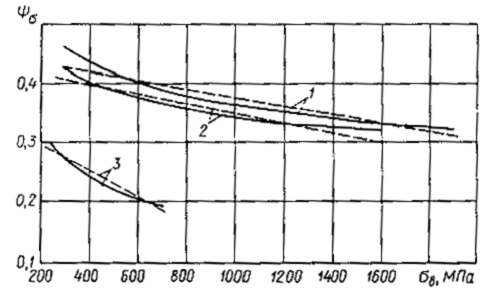
Рис. 2.12. Значения коэффициента при различной статической прочности конструкционных материалов: 1,2,3 – соответственно для сталей, титановых и алюминиевых сплавов; сплошные линии – расчетные данные по уравнению (2.75); штриховые – аппроксимация по формулам (2.76)...(2.78).

Указанная линейная аппроксимация приводит к максимальной ошибке оценки до 5%.

Большую точность обеспечивает аппроксимация полином 2-ой степени

, (2.79)

параметры которого представлены в табл. 2.6, где приведена также максимальная ошибка оценки .

Таблица 2.6. Значения параметров уравнения (2.79) и максимальной ошибки

Материал	a	b	c	, %
Стали	0.5085	-2.03·10^-4	5.4375·10^-8	3
Титановые сплавы	0.4676	-1,871·10^-4	5.7685·10^-8	2
Алюминиевые сплавы	0.4032	-5,4783·10^-4	3.6833·10^-7	1

Таким образом, из теоретического анализа следует, что с увеличением статической прочности конструкционного материала внутри одной группы коэффициент уменьшается. Причем эта закономерность проявляется в теоретических расчетах при использовании любого из известных уравнений диаграммы предельных амплитуд и линии регрессии между пределом выносливости и статической прочностью. Поэтому ограниченные по объему экспериментальные данные, опубликованы в книге [16], говорящие о росте величины с увеличением σ_в, следует считать заблуждением, объясняющимся указанным выше разбросом этой характеристики при применении ныне действующей методики усталостных испытаний.

Как показывает анализ уравнений (2.71)...(2.75), увеличение расчетного значения с ростом статической прочности материалов возможно только в том случае, если отношение будет увеличиваться с повышением статической прочности материалов, что противоречит опытным данным и уравнениям (2.2), (2.3) и (2.12). Если принять, как это было сделано Р. Хейвудом [3], постоянное отношение для всех марок сталей = 0.5, то расчетные значения окажутся также постоянными.

В частности, для всех марок сталей уравнение Р. Хейвуда [3] приводит к одинаковому значению = 0.26.

Как уже отмечалось, коэффициент чувствительности материала к асимметрии цикла оценивается на основании пределов выносливости при симметричном и отнулевом циклах напряжений. Однако, в расчетах на прочность и при схематизации циклов нагружения этот коэффициент используется и для других уровней асимметрии цикла напряжений. Более правильно, в этом случаи следует использовать изменяющийся коэффициент чувствительности к асимметрии нагружения, который можно представить в виде

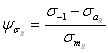(2.80)

где и - предельные амплитуда и среднее напряжение цикла для заданного коэффициента асимметрии .

С учетом уравнения диаграммы предельных амплитуд (2.58) значение подсчитывается методом последовательных приближений по формуле

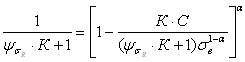, (2.81)

где

Как показывали расчеты (рис. 2.13), наибольшее отклонение от имеет у алюминиевых сплавов так при R = 0.7...0.9 отношение составляет 1.15...1.35.

Причем, величина этого отношения практически не зависит от предела прочности сплавов. Для значений R = - 1.2...- 0.5 отношение указанных коэффициентов у алюминиевых и титановых сплавов, а также сталей составляет 0.93...0.97.

Максимальное значение соответствует R = 1 и может быть подсчитано по формуле

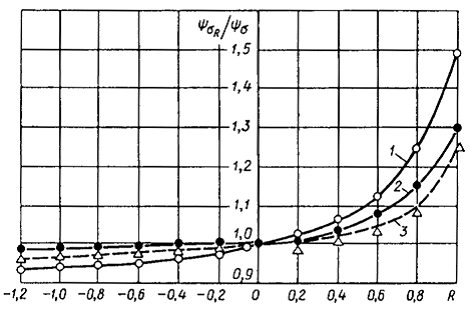
Рис. 2.13. Зависимости коэффициента от степени асимметрии цикла напряжений: 1, 2, 3 – расчетные данные по уравнению (2.81) соответственно для алюминиевых, титановых сплавов и сталей

Таким образом, теоретический анализ и экспериментальные данные показывают на снижение величины коэффициента чувствительности к асимметрии цикла напряжений с ростом статической прочности материала. В связи с этим, оказываются неприемлемыми рекомендации стандарта [14] и других источников [8, 16] по методике оценки коэффициента .

Теоретически обосновано и экспериментально подтверждено уравнение диаграммы предельных амплитуд (2.58) для металлических конструкционных материалов. Ранее известные и широко используемые на практике уравнения диаграммы (1.8), (1.9), (1.11) и (1.12) находятся в противоречии с опытными данными.

2.8. Расчетный метод оценки эффективного коэффициента концентрации напряжений

Эффективный коэффициент концентрации напряжений

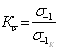(2.82)

в случае его экспериментального определения требует испытания на усталость двух серий образцов одинакового диаметра. На основании испытаний гладких стандартных образцов (первая серия) определяют предел выносливости , характеризующий свойства материала.

Испытания на усталости второй серии образцов, несущих на себе концентратор напряжений, позволяет определить предел выносливости , который зависит как от свойств материала, так и от характера и степени концентрации напряжений.

Длительность испытаний на усталость и их высокая стоимость определяют необходимость разработки расчетных методов оценки эффективного коэффициента концентрации напряжений.

Оценку эффективного коэффициента концентрации напряжений часто определяют путем использования коэффициента чувствительности материала к концентрации напряжений:

, (2.83)

. (2.84)

Однако, как показывают многочисленные результаты экспериментов, коэффициент чувствительности к концентрации напряжений (, ) не является константой материала и зависит от ряда дополнительных факторов (градиента напряжений в зоне концентрации, базы испытаний, вероятности разрушения и др.). Тем не менее, оценка и по формулам (2.83) и (2.84) возможна в первом приближении. Погрешность оценки в этом случаи может достигать 20%.

2.8.1. Метод Г. Нейбера

Для оценки эффективного коэффициента концентрации напряжений в случаи V-образного концентратора Нейбер предложил следующую эмпирическую зависимость:

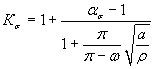, (2.85)

где a – постоянная величина для данного материала, имеющая размерность длины, — радиус кривизны у основания надреза, — входящий угол V-образного надреза, выражающийся в радианах.

Формула (2.85) не нашла широкого применения из-за значительных погрешностей и, особенно, в случаях тупых углов V-образного надреза и малых радиусов закругления [3].

2.8.2. Метод Р.Петерсона

На основании принятой гипотезы о том, что выносливость зависит от напряжения на некотором заданном расстоянии от поверхности, Петерсон получил следующую формулу для расчета величины эффективного коэффициента концентрации напряжений:

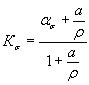, (2.86)

где - радиус кривизны дна надреза, a – постоянная материала, имеющая размерность длины и существенно зависящая от критической глубины, на которой измеряется напряжение.

К сожалению это постоянная очень сильно зависит от состояния стали (для закаленных углеродистых сталей a=0.0623 мм, для нормализованных сталей a=0.254 мм).

Для одного и того же состояния материала, но для разных видов полуфабрикатов (профиль, лист) величина a может различаться в 5...6раз [3]. Это обстоятельство затрудняет использование формулы (2.86).

2.8.3. Метод Р. Хейвуда

Для расчетной оценки эффективного коэффициента концентрации напряжений Р. Хейвуд [3] рекомендует использование следующей эмпирической формулы:

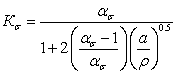, (2.87)

где a – коэффициент ослабления концентрации напряжений, выраженный в мм, величина которого зависит от вида концентратора и статической прочности сталей.

Для стальных цилиндрических образцов с поперечным отверстием диаметром при симметричном растяжении-сжатии эмпирически установлено, что

, (2.88)

где a – выражено в мм, а в МПа.

Средняя арифметическая ошибка оценки в том случае составляет .

Для стальных образцов с галтелью при симметричном растяжении-сжатии

, (2.89)

средняя арифметическая ошибка оценки при этом, как показал анализ опытных и расчетных значений, составляет 11%.

В случае стальных образцов с кольцевой выточкой в указанных выше условиях нагружения

, (2.90)

при этом 17%.

Для образцов из алюминиевых сплавов с любыми из перечисленных концентраторов напряжений при 455 МПа

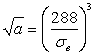, (2.91)

а при 455 МПа - =0.25^0.5 или a=0.0625 мм.

Эффективный коэффициент концентрации напряжений в этом случаи оценивают для базы N=10⁷ циклов. Погрешность расчетной оценки для алюминиевых сплавов по формуле (2.87) составляет в среднем 19%.

2.8.4. Метод Зибеля-Штилера (по ГОСТ 25.504-82)

Эффективные коэффициенты концентрации напряжений для сталей с погрешностью до 20% могут оцениваться по формулам

(2.92)

(2.93)

Коэффициент n вычисляют по формуле

(2.94)

или по графику рис. 2.14 в зависимости от значений относительного градиента в мм^-1 (см. п. п. 1.4.20 и 1.4.22) и предела текучести в МПа.

Значения относительного градиента напряжений в зависимости от типа деформации и геометрии объекта определяют по формулам, приведенным в таблице 2.7.

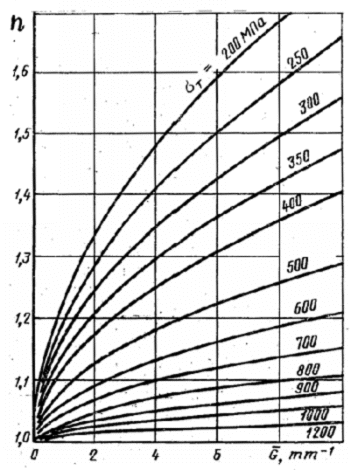
Рис. 2.14. Значения коэффициента n, вычисленные по формуле 2.94

Таблица 2.7. Формулы для вычисления значений относительного градиента напряжений

Эскиз детали	Относительные размеры	Изгиб	Растяжение-сжатие	Кручение
				-
				-
				-
				-
	-	-		-

Примечание к таблице 2.7:

.

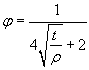Формулы (1), (2), (4), (6), (7) получены из соответствующих решений Нейбера. Формула (4) получена Н.В. Макаровой из решений Нейбера. Формулы (3), (8), (9) записаны по аналогии с формулой (4).

Формула (12) получена А.К. Прейссом.

Формулы (11), (13), (14), (15), (17), (18), (19), (20) записаны по аналогии с соответствующими формулами для образцов с выточкой или двусторонними надрезами.

Формула (21) получена поляризационно-оптическим методом Валем и дает результаты, близкие к полученным из решения Гоуланда.

2.8.5. Метод В.П. Когаева

В отличии от эмпирических методов, изложенных в п.п. 2.8.1...2.8.5, метод В.П. Когаева [8] носит теоретический характер и хорошо согласуется с экспериментальными данными для широкого круга конструкционных материалов.

Эффективный коэффициент концентрации напряжений в соответствии в методом В.П. Когаева [8] при переменном изгибе и растяжении-сжатии определяют по формуле

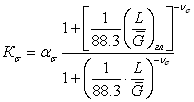, (2.95)

где L - периметр рабочего сечения образца (детали) или его часть, в точках которого действуют максимальные напряжения, в мм; - критерий подобия усталостного разрушения для гладкого образца, поперечные размеры которого равны размерам детали, в мм²; - критерий подобия усталостного разрушения детали, в мм²; величина 88.3 — критерий подобия усталостного разрушения гладкого лабораторного стандартного образца диаметром d₀=7.5 мм,

;

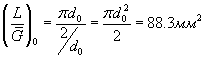- параметр уравнения подобия усталостного разрушения, являющейся постоянной для данного материала (при определенной температуре, частоте и базе испытания), определяющий чувствительность к концентрации напряжений и влиянию абсолютных размеров поперечного сечения при изгибе или при растяжении-сжатии.

Значения для различных конструкционных материалов, найденные экспериментальным путем для базы N=10⁷ циклов, приведены в таблице 2.8 [8].

Для других баз испытания параметр , как установил Агамиров Л.В. [24], вычисляют по формуле

, (2.96)

где и - пределы выносливости соответственно для базы 10⁷ циклов и рассматриваемой базы N.

При отсутствии опытных данных для конструкционных сталей величину приблизительно вычисляют по формуле [8]

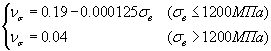(2.97)

При кручении эффективный коэффициент концентрации напряжений вычисляют по формуле, аналогичной (2.95), путем замены на . Величину определяют по таблице 2.8 или приблизительно принимают равной .

Таблица 2.8. Значения параметра уравнения подобия усталостного разрушения и .

Материал	Вид деформации	, МПа	, МПа
Осевая сталь	Изгиб	———	252	0,18
Углеродистая сталь SAE 1035	Изгиб	———	274	0,10
Углеродистая сталь SAE 1020	Изгиб	———	232	0,11
Сталь 45, t = 20 ^0C	Изгиб	———	442	0,19
Сталь 45, t = - 60 ^0C	Изгиб	———	460	0,23
Углеродистая сталь	Изгиб	———	253	0,10
Сталь 45	Изгиб	———	272	0,11
Сталь 45	Изгиб	———	309	0,11
Легированная сталь CNCM	Изгиб	———	352	0,04
Легированная сталь SAEX 4130	Изгиб	———	488	0,05
Сталь 40X и 40XН	Изгиб	———	437	0,10
Легированная сталь SAEX 2345	Изгиб	———	250	0,07
Легированная сталь	Изгиб	———	385	0,06
Коррозионно-стойкая сталь 18-8, t = 450 ^0C	Изгиб	———	240	0,30
Коррозионно-стойкая сталь 18-8, t = 630 ^0C	Изгиб	———	240	0,27
Углеродистая сталь	Изгиб	———	269	0,14
Легированная сталь	Кручение	———	327	0,29
Углеродистая сталь	Кручение	———	160	0,20
Сталь 45	Кручение	———	196	0,19
Сталь 45	Изгиб	660	307	0,10
Сталь 40X	Изгиб	2020	840	0,11
Модифицированный чугун	Изгиб	830	350	0,15
Модифицированный чугун	Кручение	830	262	0,28
Сталь 30XГСНА	Изгиб	———	730	0,10
Алюминиевый сплав АВТ	Изгиб	364	135	0,08
Алюминиевый сплав В95	Изгиб	618	174	0,09
Алюминиевый сплав АД33	Изгиб	333	127	0,09
Алюминиевый сплав Д16	Изгиб	523	184	0,08
Магниевый сплав ВМ65	Изгиб	267	113	0,10
Магниевый сплав МЛ5	Изгиб	221	67	0,30
Алюминиевый сплав ВД17	Изгиб	483	170	0,085
Алюминиевый сплав АК6	Изгиб	460	148	0,06
Алюминиевый сплав АКЧ-1	Изгиб	381	150	0,09
Титановый сплав ВТ22	Изгиб	———	560	0,07
Титановый сплав ОТ4	Изгиб	———	390	0,02
Титановый сплав ПТ38	Изгиб	———	246	0,21

2.9. Расчетный метод оценки коэффициента влияния абсолютных размеров поперечного сечения при отсутствии концентрации напряжений

Коэффициент влияния абсолютных размеров в случае экспериментального определения требует испытаний на усталость двух серий гладких образцов. Одна серия образцов имеет диаметр 7.5...10 мм, диаметр другой серии соответствует размеру поперечного сечения детали.

Разработанная В.П. Когаевым теория подобия усталостного разрушения позволяет оценивать указанный коэффициент расчетным методом [8] по уравнению для переменного изгиба и растяжения-сжатия

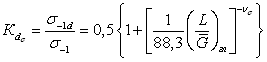, (2.98)

параметры которого аналогичны параметрам уравнения (2.95).

В случаи переменного кручения вычисляют по уравнению (2.98) путем замены на .

2.10. Расчетный метод оценки коэффициента, учитывающего совместное влияние концентрации напряжений и абсолютных размеров поперечного сечения

Расчетная оценка указанного коэффициента стала возможной на основании теории подобия усталостного разрушения В.П. Когаева [8].

Величину коэффициента при переменном изгибе и растяжении-сжатии оценивают по следующей формуле [8]:

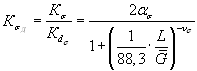(2.99)

или, исходя из модифицированной модели подобия усталостного разрушения Агамирова Л.В. [24], по уравнению

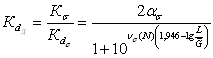(2.100)

Для случая переменного кручения коэффициент совместного влияния концентрации напряжений и абсолютных размеров поперечного сечения детали оценивают по формулам (2.99) и (2.100) путем замены на .

2.11. Расчет предела выносливости детали при симметричном цикле нагружения с учетом технологических и конструкционных факторов. Метод В. П. Когаева

При переменном изгибе и растяжении-сжатии в случаи симметричного цикла нагружения предел выносливости детали оценивают по формуле

, (2.101)

где - медианное значение предела выносливости по совокупности всех плавок металла, вычисляют по формуле (2.3); K - коэффициент снижения предела выносливости, вычисляют по формуле

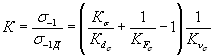(2.102)

где - коэффициент влияния шероховатости поверхности; - коэффициент влияния поверхностного упрочнения.

2.11.1. Коэффициент влияния шероховатости поверхности

Коэффициент влияния шероховатости поверхности сталей определяют либо по графику (рис.2.15) либо по формуле [8]

, (2.103)

где R_z — высота неровностей в мкм, - предел прочности в МПа.

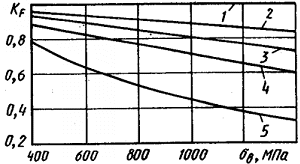
Рис 2.15. Зависимость коэффициента влияния шероховатости поверхности от предела прочности стали:
1- полирование, 2 - шлифование; 3 - тонкое точение; 4 - грубое точение; 5 - наличие окалины.

Значение коэффициента влияния шероховатости поверхности для деформируемых алюминиевых сплавов приведены в таблице 2.9 [1].

Таблица 2.9. Значения коэффициента для деформируемых алюминиевых сплавов

Окончательная обработка	Высота неровностей Rz, мкм
Полирование	0.5-1	1.00
Шлифование	1.5-2	0.96-0.98
Чистое точение	4-10	0.87-0.94
Точение	10-15	0.84-0.88
Грубое точение	20-30	0.78-0.83
Очень грубое точение	50-100	0.70-0.75

Коэффициент влияния шероховатости поверхности при переменном кручении вычисляют по формуле [8]

2.11.2. Коэффициент влияния поверхностного упрочнения

Коэффициент влияния поверхностного упрочнения для сталей определяют на основании данных, приведенных в таблице 2.10 [8].

Таблица 2.10. Влияние технологических методов поверхностного упрочнения на пределы выносливости сталей при переменном изгибе и растяжении-сжатии

Поверхностная закалка с нагрева ТВЧ (глубина закаленного слоя 0,9-1,5 мм)
		для образца диаметром, мм
	Вид образца	7-20	30-40
	Без концентрации напряжений	1.30 – 1.60	1.20 – 1.50
	С концентрацией напряжений	1.60 – 2.80	1.50 – 2.50
Химико-термическая обработка
Характеристика химико-термической обработки	Вид образца	для образца диаметром, мм
		8 – 15	30 – 40
Азотирование при глубине слоя 0,1–0,4 мм	Без концентрации напряжений	1.15 – 1.25	1.10 – 1.15
	С концентрацией напряжений (поперечное отверстие, надрез)	1.90 – 3.00	1.30 – 2.00
Цементация при глубине слоя 0.2–0.6 мм	Без концентрации напряжений	1.20 – 2.10	1.10 – 1.50
	С концентрацией напряжений	1.50 – 2.50	1.20 – 2.00
Цианирование при глубине слоя 0.2 мм	Без концентрации напряжений	1.80	-
Поверхностный наклеп
Способ обработки	Вид образца	для образца диаметром, мм
		7 – 20	30 – 40
Обкатка роликом	Без концентрации напряжений	1.20 – 1.40	1.10 – 1.25
	С концентрацией напряжений	1.50 – 2.20	1.30 – 1.80
Обдувка дробью	Без концентрации напряжений	1.10 – 1.30	1.10 – 1.20
	С концентрацией напряжений	1.40 – 2.50	1.10 – 1.50

Поверхностное пластическое деформирование (обработка роликами, обдувка дробью, алмазное выглаживание и т. д.) магниевых и алюминиевых сплавов при отсутствии концентрации напряжений обеспечивает значение =1.25...1.30.

При наличии концентрации напряжений = (0.7...0.9) , где — теоретический коэффициент концентрации напряжений [1].

Нижнее значение сомножителя при соответствует высоким уровням концентрации напряжений ( = 2.5...3.5), а верхние значения – для <2.0.

Расчет предела выносливости при переменном кручении производят по формулам (2.101) и (2.102) путем замены на .

2.12. Расчетный метод оценки коэффициента чувствительности к асимметрии цикла напряжений с учетом технологических и конструкционных факторов

Изложенная ранее методика расчета и даёт возможность оценить эту характеристику для гладких лабораторных образцов из рассматриваемого конструкционного материала, т.е. без учёта влияния конструкционных и технологических факторов. Для реальных же деталей машин и элементов конструкций расчёт коэффициента чувствительности к асимметрии цикла напряжений в соответствии с [8,14] производят по формулам

; , (2.104)

где и — коэффициенты чувствительности к асимметрии цикла конструкционного материала, определяемые по методике, изложенной выше; К - коэффициенты снижения предела выносливости, вычисляемые по формуле (2.102).

2.13. Расчетный метод построения диаграммы предельных амплитуд при наличии концентрации напряжений

Единого мнения о методике расчетного построения диаграммы предельных амплитуд для образцов с концентрацией напряжений не существует, в основном, в связи с ограниченным объёмом соответствующих экспериментальных данных.

Известные методы расчёта координат точек диаграммы предельных амплитуд [3, 7, 11, 17] при наличии концентрации напряжений базируется на предварительно построенной расчётом [11] или экспериментально [3, 7, 17] диаграмме для гладких образцов, координаты точек которой уменьшают в и раз (рис. 2.16). Величины и представляют собой эффективные коэффициенты концентрации по амплитуде и среднему напряжению предельного цикла, т. е.

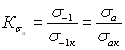и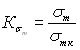, (2.105)

где , , — соответственно номинальные значения предела выносливости, предельной амплитуды и предельного среднего напряжения цикла образцов с концентратором напряжений.

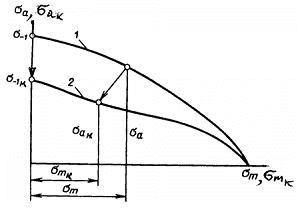
Рис. 2.16. Диаграммы предельных амплитуд для гладких образцов (кривая 1) и образцов с концентратором напряжений (кривая 2).

Расхождения в существующих методах расчётного построения диаграммы предельных амплитуд с учётом концентрации напряжений [3, 7, 11, 17] заключаются в различных подходах к определению эффективных коэффициентов концентрации (2.105) на различных участках диаграммы.

2.13.1. Метод Серенсена С.В., Кинасошвили Р.С.

С.В. Серенсеном, Р.С. Киносошвили и позднее В. П. Когаевым [3] на основании обобщения результатов испытаний стальных образцов с концентраторами напряжений при асимметричном осевом нагружении сделан вывод о возможности принятия

и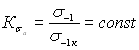

для всего диапазона значений средних напряжений (рис.2.17). Следует отметить, что этот подход широко используется при определении коэффициента запаса прочности деталей, работающих в условиях переменных напряжений.

Как показал последующий анализ опытных данных, построенные таким образом диаграммы предельных амплитуд для деформируемых алюминиевых сплавов содержат значительную систематическую ошибку, приводящую к завышению расчётного значения коэффициента запаса, связанную с недооценкой влияния концентратора на величину среднего напряжения предельного цикла (таблица 2.11).

Аналогичные результаты следует ожидать и для сталей, если к анализу привлечь белее представительный экспериментальный материал, чем рассмотренный в работе [7].

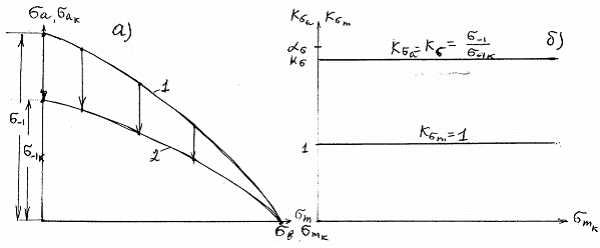
Рис. 2.17. Схема построения диаграммы предельных амплитуд при наличии концентрации напряжений:
а) диаграммы предельных амплитуд гладких образцов (1) и образцов с концентратором напряжений (2);
б) значения эффективных коэффициентов концентрации.

2.13.2. Метод Ганна

К.Ганн [17] предложил графический метод построения диаграммы предельных амплитуд образцов с концентрацией напряжений (рис. 2.18)

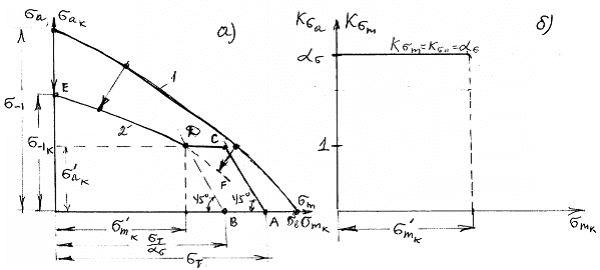
Рис. 2.18. Схема построения диаграммы предельных амплитуд при наличии концентрации напряжений:
а) диаграммы предельных амплитуд гладких образцов (1) и образцов с концентратором напряжений (2);
б) значения эффективных коэффициентов концентрации.

Вначале строят расчётным или экспериментальным путем диаграмму предельных амплитуд цикла напряжений для гладких лабораторных образцов (рис. 2.18,а). Из точки А, абсцисса которой равна пределу текучести материала , проводят луч под углом 45⁰. Точки этого луча соответствуют циклам, для которых максимальные напряжения в гладких образцах и максимальные напряжения в надрезанных образцах после полного их перераспределения из-за пластического деформирования в зоне концентрации равны пределу текучести материала.

Аналогичный луч проводят из точки В. Точки этого луча соответствуют действительным максимальным напряжениям циклов, действующим в точках наибольшей концентрации в надрезанных образцах, равным пределу текучести.

При построении диаграммы предельных амплитуд с учётом концентрации напряжений (линия ЕДF на рис. 2.18, а) принимают

.

Окончательно в качестве диаграммы предельных амплитуд циклов напряжений для образцов с концентраторами рассматривают линию ЕДСА. Участок ЕД соответствует упругим деформациям при действии максимальных нагрузок.

Анализ опытных данных показывает, что методика построения диаграммы предельных амплитуд, предложенная К.Ганном, приводит к заметному занижению расчётных значений предельных амплитуд цикла напряжений для образцов с концентратором (таблица 2.11).

2.13.3. Метод Хейвуда

Р.Б. Хейвуд [3] также рассматривает случай, когда

,

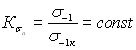однако значение эффективного коэффициента концентрации средних напряжений принимает в зависимости от уровня (см. рис. 2.19).

Величину этого коэффициента рекомендуется [3] подсчитывать методом последовательных приближений по формуле

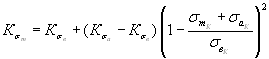, (2.106)

где - номинальное значение предела прочности образцов с концентратором напряжений,

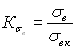- эффективный коэффициент концентрации по пределу прочности.

Для материалов с определенным запасом пластичности, к которым относятся конструкционные стали и деформируемые алюминиевые, магниевые и титановые сплавы, Р.Хейвуд рекомендует принять . В этом случае формула (2.106) запишется в виде

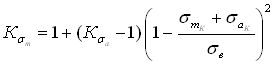. (2.107)

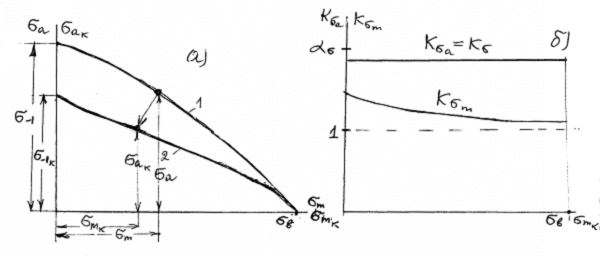
Рис. 2.19. Схема построения диаграммы предельных амплитуд при наличии концентрации напряжений: а) диаграммы предельных амплитуд гладких образцов (1) и образцов с концентратором напряжений (2); б) значения эффективных коэффициентов концентрации.

Формулы (2.106) и (2.107) Р. Хейвуд выбрал из большого ряда аналогичных формул, полученных на основании удовлетворения граничным условиям и других логических построений, как наиболее близко соответствующие опытным данным.

Недостатком изложенного метода построения диаграммы предельных амплитуд образцов с концентратором напряжений является то обстоятельство, что эффективный коэффициент концентрации средних напряжений заметно ниже эффективного коэффициента концентрации амплитуд даже при малой асимметрии цикла и что он непрерывно убывает по мере роста средних напряжений даже в том случае, когда максимальные напряжения цикла в зоне концентрации существенно ниже значения предела текучести материала, т.е.в случае упругих деформаций при циклическом нагружении. Появление пластических деформаций, приводящих к перераспределению напряжений в зоне концентрации, никак не отражается на значении коэффициента и поведении диаграммы предельных амплитуд.

Анализ опытных данных показывает, что метод построения диаграммы предельных амплитуд с учётом концентрации напряжений, предложенный Р. Хейвудом [3], приводит к завышению расчетных значений предельных амплитуд цикла напряжений (таблица 2.11).

2.13.4. Метод Степнова М.Н.

Автор настоящей работы [11] предложил метод построения диаграммы предельных амплитуд для образцов с концентраторами напряжений, который включает в себя положительные элементы рассмотренных выше подходов [3, 7, 17] и свободен от их недостатков.

Вначале по уравнению (2.59) строят диаграмму предельных амплитуд для гладких образцов (линия АВСD на рис. 2.20).

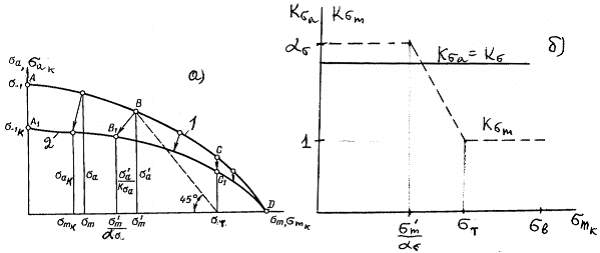
Рис. 2.20. Схема построения диаграммы предельных амплитуд при наличии концентрации напряжений:
а) диаграммы предельных амплитуд гладких образцов (1) и образцов с концентрацией напряжений (2);
б) значения эффективных коэффициентов концентрации.

В соответствии со значением предела текучести диаграмму предельных амплитуд делят на три участка. На участке АВ предельные максимальные напряжения цикла не превышают предела текучести материала . Для участка СD характерно превышение средними напряжениями цикла величины . Для среднего участка ВС предельные максимальные напряжения , а .

В соответствии с тремя участками диаграммы предельных амплитуд для гладких образцов строят три участка диаграммы A₁B₁C₁D для образцов с концентраторами напряжений. Причём, для всех трёх участков принимают

.

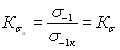Значение этого коэффициента оценивают расчётным методом (см. параграф «Расчетный метод оценки эффективного коэффициента концентрации напряжений»), либо определяют экспериментально. Эффективный коэффициент концентрации средних напряжений цикла для каждого участка принимает различные значения.

Для участка A₁B₁ только упругих деформаций принимают

.

Уравнение кривой A₁B₁ в соответствии с формулой (2.58) имеет вид:

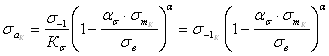. (2.108)

Для участка C₁D эффективный коэффициент концентрации средних напряжений принимают равным единице

,

так как при за счет пластических деформаций происходит выравнивание распределения напряжений в зоне концентратора.

Уравнение кривой C₁D принимает вид:

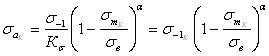. (2.109)

На среднем участке B₁C₁ диаграммы эффективный коэффициент концентрации средних напряжений меняется от в точке B₁ до единицы в точке C₁, так как за счет пластических деформаций происходит частичное выравнивание эпюры напряжений.

Для упрощения построения этого участка диаграммы целесообразно принять изменение коэффициента по линейному закону. В этом случае

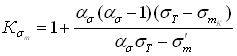. (2.110)

Значение определяется из условия или

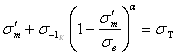, (2.111)

либо графическим путем (см. рис. 2.20 б).

Уравнение среднего участка B₁C₁ имеет вид:

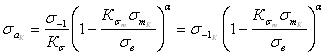. (2.112)

Уравнение (2.112) носит общий характер и может быть использовано для всех трех участков диаграммы с учетом изменения параметра , который выражается формулой

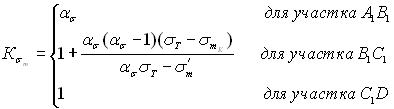(2.113)

На рис. 2.21 для иллюстрации предлагаемой методики показаны построенные расчётным путем диаграммы предельных амплитуд образцов с различной степенью концентрации напряжений. Соответствие экспериментальных [18,19] и расчётных значений предельных амплитуд вполне удовлетворительно.

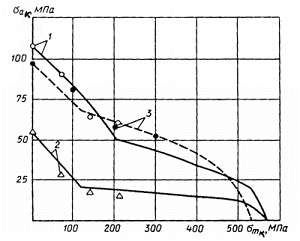
Рис. 2.21. Схема построения диаграммы предельных амплитуд при наличии концентрации напряжений:
линии – расчёт по формуле (2.112); точки – эксперимент: , — работа [18]; — работа [19];
1 — сплав 75S — T6; =2.0, =1.94;
2 – сплав 75S — T6; =4.0, =3.86;
3 — сплав Д16; =2.18, =1.85.

Для количественной оценки точности рассмотренных в настоящем разделе методов расчёта ординат диаграммы предельных амплитуд для образцов с концентраторами напряжений были сопоставлены расчетные и экспериментальные значения предельных амплитуд на основании 40 кривых усталости, построенных для образцов с различной степенью концентрации напряжений из деформируемых алюминиевых сплавов, испытанных при асимметричном осевом нагружении.

В результате этого сопоставления вычислены значения относительных систематической и средней квадратической ошибок (таблица 2.11) для базы испытаний N = 10⁷ циклов, которые подсчитывались по формулам

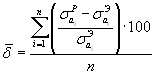, в % (2.114)

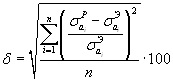, в % (2.115)

где и — соответственно расчетные и экспериментальные значения предельных амплитуд цикла напряжений для базы N = 10⁷ циклов при наличии концентрации напряжений.

Таблица 2.11. Значения систематической и средней квадратической ошибок оценивания предельных амплитуд различными методами

Ошибка	Значение ошибки, %, при расчете по методу
	Серенсена С. В. и др. [7]	Ганна К. [17]	Хэйвуда Р. Б. [3]	Степнова М. Н. [11]
	+ 34,6	- 14,6	+ 13,3	+ 0,5
	48,2	22,8	24,7	17,2

Как следует из таблицы 2.11, метод [7] непригоден для расчета предельной амплитуды цикла образцов с концентраторами напряжений из деформируемых алюминиевых сплавов. Погрешность метода из-за большой систематической ошибки отрицательно скажется на надежности элементов конструкций, рассчитанных на усталость с использованием найденных таким образом оценок характеристик сопротивления усталости при наличии концентрации напряжений.

Методы Ганна [17] и Хэйвуда [3] по степени соответствия экспериментальным данным являются равноценными, однако, подход Ганна приводит к более осторожным результатам из-за отрицательного знака систематической ошибки.

Метод Степнова [11] для расчета предельной амплитуды цикла для образцов из деформируемых алюминиевых сплавов при наличии концентрации напряжений практически не содержит систематической ошибки и обеспечивает наименьшую случайную погрешность по сравнению с другими известными методами. Уровень случайной ошибки =17,2% не следует считать высоким из-за большого разброса экспериментальных значений предельных амплитуд цикла напряжений при испытании на осевое растяжение-сжатие как гладких образцов, так и в особенности образцов с концентраторами напряжений.

2.14. Расчетный метод оценки коэффициента чувствительности к асимметрии цикла напряжений с учетом их концентрации

Выше был рассмотрен метод оценки коэффициента чувствительности детали к асимметрии цикла нагружения с учетом комплекса конструкционных и технологических факторов. Однако, широкого теоретического или экспериментального обоснования этот метод не получил, хотя и нашел применение на практике.

В настоящем разделе с учетом материала, изложенного в п.2.13, дается теоретическое обоснование оценки влияния концентрации напряжений на уровень коэффициента чувствительности детали к асимметрии нагружения для рассмотренных выше подходов к построению диаграммы предельных амплитуд при наличии концентрации напряжений.

В соответствии с формулой (2.104) при отсутствии других факторов, влияющих на величину К, коэффициент чувствительности к асимметрии цикла нагружения при наличии концентратора напряжений определяется соотношением

. (2.116)

Опытные данные, заимствованные из ряда литературных источников различных авторов и представленные на рис. 2.22, и результаты проведенных корреляционного и регрессионного анализов [4] указывают на отсутствие зависимости, представленной формулой (2.116). Так, например, коэффициент корреляции между случайными величинами и оказался незначимо отличающимся от нуля (r = -0.066 при =0,457). Поэтому линия регрессии 1на рис. 2.22 почти горизонтальна. Более того, она проходит заметно выше линии с ординатами точек, равных единице, что говорит о более высокой чувствительности материала к асимметрии цикла при наличии концентрации напряжений в образцах. Обращает на себя внимание значительный разброс экспериментальных данных вокруг линии регрессии. Мера индивидуального рассеяния составляет =0.43.

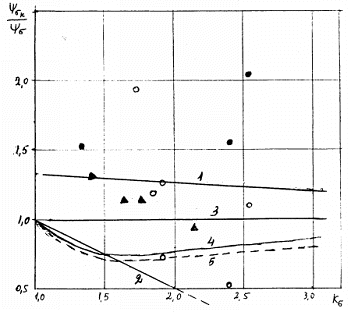
Рис. 2.22. Величины отношения для различных значений коэффициента концентрации напряжений :
Точки — эксперимент: — алюминиевые сплавы,  — титановые сплавы, — стали;
Линии — расчет: 1 — на базе регрессионного анализа,
2 — по формуле (2.119),
3 — по методике К.Ганна,
4 — по методике Р.Хэйвуда для алюминиевых сплавов,
5 — по методике Р.Хэйвуда для сталей.

При использовании для построения диаграммы предельных амплитуд метода С.В.Серенсена, Р.С.Киносошвили и В.П.Когаева уравнение диаграммы с учетом концентрации напряжений в соответствии с (2.3) и (2.33) будет иметь вид

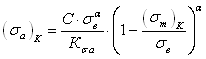. (2.117)

В этом случае коэффициент чувствительности к асимметрии цикла напряжений

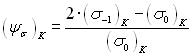, (2.118)

где и — пределы выносливости образцов с концентраторами напряжений при симметричном и отнулевом циклах соответственно, вычисляют методом последовательных приближений из уравнения

. (2.119)

Для всех рассмотренных конструкционных материалов (алюминиевые и титановые сплавы, стали) величина , найденная из уравнения (2.119), примерно в раз ниже соответствующей характеристики для гладких образцов, причем, коэффициент монотонно убывает с ростом предела прочности материала.

Сопоставление расчетных значений и результатов экспериментов для алюминиевых сплавов показало, что рассмотренный метод дает значительное (от 2 до 5 раз) занижение коэффициента чувствительности к асимметрии цикла нагружения по сравнению с опытными данными. Аналогичные результаты следует ожидать и для других конструкционных материалов. На рис.2.22 расчетные данные по формуле (2.119) показаны линией 2.

В связи с этим соответствующие рекомендации действующего стандарта должны быть подвергнуты корректировке.

Использование метода К. Ганна для построения диаграммы предельных амплитуд цикла нагружения при наличии концентрации напряжений в пределах упругих деформаций, что имеет место при предельном отнулевом цикле, приводит к следующему уравнению диаграммы:

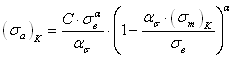. (2.120)

Коэффициент чувствительности к асимметрии цикла образца с концентратором напряжений с учетом (2.120) вычисляют с помощью уравнения

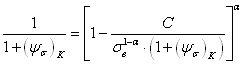, (2.121)

которое в точности совпадает с уравнением (2.75), соответствующим гладким лабораторным образцам. Таким образом, из метода К.Ганна следует вывод о равенстве коэффициентов чувствительности к асимметрии цикла напряжений гладких и надрезанных образцов, то есть , что так же не согласуется с имеющимися опытными данными. На рис.2.22 расчетные данные по формуле (2.121) представлены линией 3.

Рассмотренный ранее метод Р. Хэйвуда для построения диаграммы предельных амплитуд цикла напряжений при наличии концентратора напряжений определяет следующий вид уравнения диаграммы:

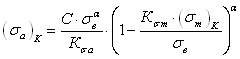, (2.122)

которое приводит к уравнению для вычисления коэффициента чувствительности к асимметрии цикла напряжений в виде

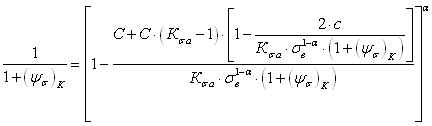(2.123)

В качестве примера в таблице 2.12 приведены результаты расчетов по формуле (2.123) значений для сталей различной прочности и величины эффектного коэффициента концентрации напряжений .

Таблица 2.12. Значения коэффициента чувствительности к асимметрии цикла напряжений для сталей, вычисленные по уравнению (2.123).

	1,0	1,1	1,3	1,5	2,0	3,0	4,0
, МПа
300	0,489	0,447	0,389	0,354	0,319	0,325	0,346
600	0,430	0,395	0,347	0,319	0,292	0,298	0,316
900	0,399	0.367	0,324	0,300	0,277	0,283	0,298
1200	0,379	0,349	0,309	0,287	0,266	0,272	0,287
1500	0,363	0,335	0,298	0,277	0,258	0,264	0,278
1800	0,351	0,325	0,289	0,270	0,252	0,258	0,271
2100	0,341	0,316	0,282	0,263	0,247	0,252	0,265

Как следует из приведенных данных, поведение коэффициента с изменением не однозначно. Так, например, для сталей с =1200 МПа при увеличении от 1,0 до 2,0 значение убывает с 0,379 до 0,266, то есть в 1.42 раза. При =2 снижение прекращается, а при дальнейшем увеличении до 4,0 коэффициент возрастает до величины 0,287. Таким образом, при =4 снижение в соответствии с уравнением (2.123) составляет лишь 1.32 раза. На рис. 2.22 расчетные данные по формуле (2.123) представлены линиями 4 и 5 для алюминиевых сплавов и сталей соответственно. Этот график демонстрирует еще большее несоответствие расчетных и опытных данных. К указанной ранее случайной ошибке (мере индивидуального рассеяния) =0.43 добавляется систематическая =0.5.

Расчетные значения коэффициента по уравнению (2.123) для алюминиевых сплавов в 1,5...2 раза меньше опытных данных. Аналогичные результаты следует ожидать и для других конструкционных материалов.

Для всех рассмотренных групп конструкционных материалов чувствительность к асимметрии цикла напряжений при наличии концентратора монотонно убывает с ростом статической прочности, как это отмечалось и для гладких образцов.

Метод расчетного построения диаграммы предельных амплитуд образцов с концентрацией напряжений автора [11], рассмотренный выше, приводит в пределах упругого деформирования (участок A₁B₁ на рис. 2.20) к уравнению диаграммы следующего вида

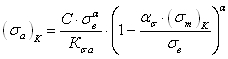, (2.124)

которое определяет расчетную формулу для ,

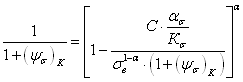. (2.125)

Как следует из уравнения (2.125), коэффициент чувствительности материала к асимметрии цикла напряжений зависит от чувствительности материала к концентрации напряжений, что учитывается в указанном уравнении наличием отношения .

Вычисленные значения для рассматриваемых групп конструкционных материалов приведены в таблице 2.13. На рис. 2.23 для наглядности показана зависимость от предела прочности сталей для различных значений отношения .

Для материалов, абсолютно чувствительных к концентрации напряжений, то есть при , формула (2.125) полностью совпадает с уравнением (2.75), что говорит о независимости коэффициента чувствительности к асимметрии цикла напряжений от степени концентрации напряжений, то есть .

Экспериментальные данные, ранее представленные на рис. 2.22, показаны на рис. 2.24 в координатах , .

Таблица 2.13. Значения коэффициента чувствительности к асимметрии цикла напряжений , вычисленные по формуле (2.125).

Материал		1,00	1,05	1,10	1,20	1,30	1,50	2,00
	, МПа
алюминиевые сплавы	100	0,420	0,443	0,465	0,512	0,558	0,653	0,898
	200	0,319	0,336	0,353	0,388	0,423	0,493	0,676
	300	0,272	0,286	0,301	0,330	0,360	0,419	0,573
	400	0,243	0,256	0,269	0,295	0,321	0,374	0,510
	500	0,223	0,234	0,246	0,270	0,294	0,342	0,467
	600	0,207	0,218	0,229	0,251	0,274	0,319	0,434
	700	0,195	0,206	0,216	0,237	0,258	0,300	0,408
титановые сплавы	300	0,423	0,445	0,466	0,510	0,554	0,642	0,865
	500	0,387	0,407	0,427	0,467	0,507	0,587	0,791
	700	0,365	0,384	0,403	0,440	0,478	0,554	0,746
	900	0,349	0,367	0,385	0,421	0,457	0,530	0,714
	1100	0,338	0,355	0,372	0,407	0,442	0,512	0,689
	1300	0,328	0,345	0,362	0,395	0,429	0,497	0,669
	1500	0,320	0,336	0,353	0,386	0,419	0,485	0,653
стали	300	0,489	0,515	0,540	0,591	0,642	0,745	1,005
	600	0,430	0,453	0,475	0,519	0,564	0,654	0,882
	900	0,399	0,420	0,440	0,482	0,523	0,607	0,818
	1200	0,379	0,398	0,417	0,457	0,496	0,575	0,775
	1500	0,363	0,382	0,401	0,438	0,476	0,552	0,743
	1800	0,351	0,369	0,387	0,424	0,460	0,533	0,718
	2100	0,341	0,359	0,376	0,412	0,447	0,518	0,698

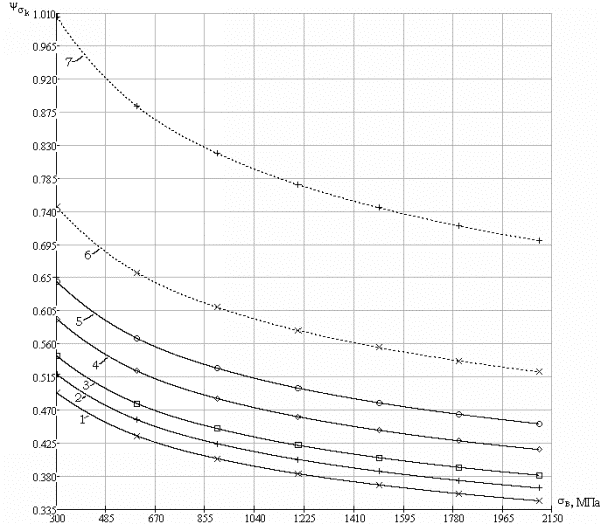
Рис. 2.23 Зависимость коэффициента чувствительности к асимметрии цикла напряжений от предела прочности сталей в связи с влиянием концентрации напряжений:
1, 2, 3, 4, 5, 6, 7 – соответственно для

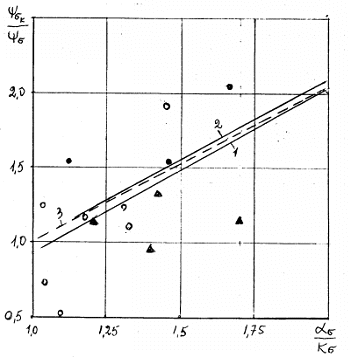
Рис. 2.24 Зависимость отношения от величины :
Точки — эксперимент: — алюминиевые сплавы,  — титановые сплавы, — стали;
Линии — расчет: 1 — на основании регрессионного анализа (линия регрессии), 2 и 3 — по уравнениям (2.125) и (2.126) соответственно для алюминиевых сплавов и сталей.

Корреляционный и регрессионный анализы этих данных указывают на наличие достаточно тесной корреляционной связи между величинами x и у. Коэффициент корреляции достиг значения r=0.514, что больше критического значения r_0.95=0.457 для уровня значимости =0.05 [4]. Мера индивидуального рассеивания снизилась до =0.367, хотя сохранилась достаточно высокой, что, как уже отмечалось выше, связано с возможными ошибками при испытании на усталость при растяжении-сжатии образцов с концентраторами напряжений.

Таким образом, для реальных конструкционных материалов, у которых , коэффициент чувствительности к асимметрии цикла напряжений при наличии концентратора увеличивается по сравнению с соответствующим значением для гладких образцов, и это увеличение тем больше, чем ниже чувствительность материала к концентрации напряжений.

Анализ расчетных данных по формуле (2.125) (таблица 2.13) и результатов регрессионного анализа показал, что вычисление можно производить по линейному соотношению

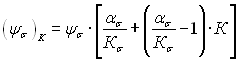, (2.126)

где К — поправочный коэффициент, равный 0.05; 0.04; 0.10 для сталей, титановых и алюминиевых сплавов соответственно.

Это уравнение не дает систематической ошибки, поскольку ее графики (2 и 3 на рис. 2.24) практически совпадают с линией регрессии (1 на рис. 2.24).

Среднее квадратическое отклонение экспериментальных результатов от рассчитанных по уравнениям (2.125) и (2.126) составляет 30...40%, при этом нужно иметь в виду, что экспериментальная ошибка при оценке путем непосредственных испытаний на усталость заметно превышает эту величину.

Приведенные данные указывают на значительное преимущество теоретического метода определения коэффициентов чувствительности к асимметрии цикла нагружения и перед экспериментальным.

Расчетный метод оценки коэффициента чувствительности к асимметрии цикла нагружения при наличии концентрации напряжений является значительно более надежным, чем другие расчетные методы (Серенсена-Кинасошвили, Ганна, Хейвуда), что определяется более обоснованной методикой построения диаграммы предельных амплитуд при наличии концентрации напряжений, изложенной в методе Степнова М.Н.

Итак, подводя итог этого параграфа необходимо отметить, что наличие концентрации напряжений увеличивает чувствительность конструкционных материалов к асимметрии цикла нагружения, которая снижается по мере роста статической прочности материала. В связи с этим возникает необходимость корректировки соответствующего раздела ГОСТа 25.504-82.

3. Методы ускоренных и форсированных испытаний на усталость

Применение ускоренных и форсированных методов испытаний на усталость вызвано необходимостью сокращения времени "доводки" новых конструкций, внедрения новой технологии производства полуфабрикатов и деталей, корректировки химического состава сплавов ит.д. По результатам таких испытаний можно выбрать оптимальные режимы технологии производства сплавов и деталей, установить наиболее целесообразные, с точки зрения прочности и долговечности, геометрические параметры силовых элементов, оценить расчетные характеристики сопротивления усталостному разрушению, определить оптимальный состав и структуру конструкционных материалов и т.д.

Рассмотренные в настоящем разделе ускоренные и форсированные методы могут быть применены для испытания на усталость образцов, моделей, деталей машин и элементов конструкций в условиях нормальной температуры, отсутствия агрессивной среды и коррозии трения.

Ускоренные и форсированные методы испытания на усталость не могут быть использованы для оценки сопротивления усталости объектов, получивших поверхностное упрочнение, в связи с возможной релаксацией остаточной напряженности при действии высоких переменных напряжений, свойственных ускоренным и форсированным методам. Нужно иметь в виду, что оценка сопротивления усталости с помощью различных методов будет надежной лишь при совпадении места и характера усталостного разрушения (по зерну или границам зерен) при обычных и ускоренных или форсированных испытаниях.

3.1. Ускоренный метод Про для оценки медианы предела выносливости

Ускоренный метод усталостных испытаний Про предусматривает испытание образцов до разрушения при линейно возрастающей амплитуде цикла напряжений. В зависимости от конструкции испытательной машины возрастание напряжений может быть ступенчатым или непрерывным (рис. 3.1).

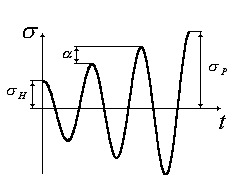
Рис 3.1. Схема испытаний с непрерывно возрастающей амплитудой цикла напряжений.

Для определения предела выносливости методом Про необходимо испытывать не менее трех-четырех серий образцов. Скорость возрастания амплитуды напряжений для каждой серии принимают различной.

Максимальную скорость нагружения выбирают с таким расчетом, чтобы напряжение σ_p в момент разрушения не превышало предела текучести материала. Минимальную скорость назначают по возможности низкой. Однако, необходимо учитывать, что длительность испытаний по методу Про определяется в основном испытаниями при минимальной скорости нагружения, т.е. эффективность рассматриваемого метода во многом зависит от уровня минимальной скорости возрастания напряжений. Обычно скорости возрастания амплитуды напряжений выбирают в диапазоне МПа/цикл.

Испытания всех серий проводят при одинаковой начальной амплитуде цикла напряжений σ_H, величину которой для чугунов и сталей выбирают на 10-15% выше предполагаемой величины предела выносливости. Для легких сплавов начальную амплитуду цикла напряжений принимают равной ожидаемой величине предела выносливости для базы 10⁷ циклов. Снижение уровня начальной амплитуды цикла напряжения по сравнению с указанными значениями уменьшает эффективность ускоренных испытаний.

Исследованиями установлено, что снижение начального уровня напряжения не оказывает значительного влияния на определяемую величину предела выносливости для материалов, не чувствительных к тренировке.

Предел выносливости при ускоренных испытаниях по методу Про определяется из уравнения

(3.1)

где - скорость возрастания амплитуды напряжения; - медиана разрушающего напряжения при испытании с данной скоростью возрастания напряжений; k, c — параметры уравнения.

Зависимость, построенная по уравнению (3.1) в координатах и , изображается прямой линией, уравнение которой

, (3.2)

где и b = k.

Для определения предела выносливости подбирают методом последовательных приближений такое значение параметра с, при котором отклонение экспериментальных точек от прямой будет минимальным.

В этом случае функция

(3.3)

должна иметь минимальное значение, т.е.

(3.4)

(3.5)

Отсюда

, (3.6)

(3.7)

В приведенных формулах и представляют собой начальные моменты величин и , вычисляемые по формулам

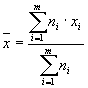, (3.8)

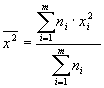, (3.9)

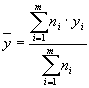, (3.10)

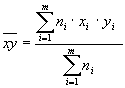, (3.11)

где m — число скоростей возрастания амплитуды напряжения; n_i — число образцов, испытанных при i-й скорости возрастания амплитуды напряжения; x_i — величина, соответствующая скорости возрастания амплитуды напряжений; y_i — медиана разрушающего напряжения при i-й скорости его возрастания.

За медиану разрушающего напряжения при нечетном числе образцов, испытанных при одной скорости возрастания амплитуды напряжений, принимается разрушающее напряжение среднего образца в вариационном ряду. При четном числе образцов медиана разрушающего напряжения определяется как полусумма разрушающих напряжений двух средних образцов в вариационном ряду.

Мерой рассеяния экспериментальных точек вокруг линии является величина Q, определяемая выражением

(3.12)

Значение параметра с выбирается так, чтобы значение Q (3.12) было минимальным (рис 3.2). Для многих материалов значение параметра с лежит в диапазоне 0.3-0.5.

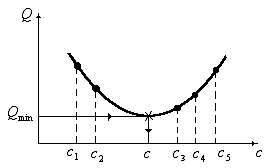
Рис. 3.2. Схема определения значения параметра с уравнения (3.1).

Для легких сплавов, сталей и чугунов систематическая ошибка при определении предела выносливости методом Про в большинстве случаев не превышает 4-6%. Случайная ошибка зависит от объема испытаний. Анализ результатов ускоренных испытаний показал, что для материалов с коэффициентом вариации предела выносливости 10% число образцов для надежного определения медианы предела выносливости должно составлять 8-12 штук. Для сплавов с >15%, требуется испытание 12-20 образцов.

Для легких сплавов величина предела выносливости, найденная из уравнения (3.1), соответствует базе 10⁷ циклов [1].

Определение предела выносливости деформируемых алюминиевых и титановых сплавов для других баз по результатам испытаний с возрастающей амплитудой напряжений может производиться с помощью уравнений (2.38) и (2.43) после предварительной оценки величины для базы 10⁷ циклов на основании формулы (3.1).

Метод Про при определении медианы предела выносливости дает экономию во времени примерно до 10 раз и не дает экономии в числе образцов по сравнению с обычным методом [20].

Определение предела выносливости по методу Про производится в следующей последовательности:

1) разрушающие напряжения для образцов, испытанных на одном уровне скорости возрастания амплитуды, располагают в порядке возрастания, то есть в вариационный ряд;

2) определяют медианы разрушающих напряжений для каждого уровня скорости возрастания амплитуды;

3) задаются рядом значений параметра с и вычисляют параметры a и b по формулам (3.6) и (3.7), и меру рассеяния экспериментальных данных вокруг прямой линии по формуле (3.12);

4) определяют значение параметра с, дающее минимум отклонения экспериментальных точек от прямой ;

5) находят предел выносливости для установленного значения параметра с.

Объем испытаний методом Про можно сократить в 1.5-2 раза при использовании заранее известного значения параметра с уравнения (3.1).

В этом случае испытания целесообразно проводить при двух скоростях возрастания амплитуды цикла напряжения.

Оценка параметра с для этой цели может быть произведена по результатам ранее проведенных испытаний на усталость аналогичных материалов и элементов конструкций.

Так, например, при переменном изгибе образцов из сталей 45 и 30ХГСА и переменном кручении образцов из высокопрочного чугуна параметр с принимает значения, близкие к 0.3 [20]. Для алюминиевых сплавов средней прочности при испытаниях на переменный изгиб можно принять с = 0.33, для высокопрочных сплавов с = 0.37 [20]. Абсолютные размеры поперечного сечения образцов не оказывают заметного влияния на величину параметра с. Концентрация напряжений приводит к снижению его значения.

Следует иметь в виду, что абсолютная погрешность в оценке значения параметра с, равная 0.1 (т.е. примерно 30%) приводит к ошибке определения предела выносливости в среднем лишь на 8-10%.

Опыт использования ускоренного метода Про указывает на возможность его применения для оценки предела выносливости образцов и натурных деталей, причем в качестве критерия разрушения можно принимать как образование макротрещины усталости определенного размера, так и окончательное разрушение.

3.2. Ускоренный метод испытания на усталость Эномото

Ускоренный метод Эномото предусматривает испытание одной серии из четырех-пяти образцов при постоянной скорости возрастания амплитуды цикла напряжений. Начальный уровень напряжения выбирается так же, как в методе Про.

Определение предела выносливости по результатам ускоренных испытаний по методу Эномото основано на предположении, что при постоянной скорости возрастания амплитуды напряжения отношение разрушающих напряжений к величине предела выносливости является постоянной величиной для материалов одного типа, т.е.

(3.13)

где - коэффициент, зависящий только от скорости возрастания амплитуды напряжения; - медиана разрушающей амплитуды цикла напряжений.

Значение коэффициента K и его средней квадратической ошибки , подсчитанные по результатам испытаний различных марок сталей и чугунов, алюминиевых и магниевых сплавов для различных скоростей возрастания амплитуд цикла напряжений, приведены в таблице 3.1.

Таблица 3.1. Значения K и при различных скоростях возрастания амплитуды цикла напряжений

Материал	10^4, МПа/цикл	K
Стали, Чугуны	0,1	1,08	0,08
	0,5	1,13	0,12
	1,0	1,18	0,14
Алюминиевые и магниевые сплавы, база 10^7циклов	0,3	1,30	0,05
	0,5	1,33	0,06
	1,0	1,38	0,07
	2,0	1,46	0,10
	4,0	1,63	0,12
	6.0	1,76	0,18

Определение предела выносливости методом ускоренных испытаний Эномото проводится в следующей последовательности:

1) разрушающие напряжения располагают в возрастающем порядке;

2) определяют медиану разрушающих напряжений аналогично методу Про;

3) в зависимости от принятой скорости возрастания амплитуды напряжения по таблице 3.1 или на основании имеющихся результатов испытаний выбирают значение коэффициента K;

4) по формуле (3.13) вычисляют значение предела выносливости.

Анализ результатов показывает, что погрешность в определении предела выносливости при использовании метода Эномото достигает 10-15%. В связи с этим указанный метод может быть использован для ориентировочной оценки предела выносливости.

3.3. Оценка предела выносливости методом Локати

Метод Локати применим для материалов, правая ветвь кривой усталости которых может быть аппроксимирована прямой линией, параллельной оси абсцисс (углеродистые стали).

Испытаниям подвергается одна серия образцов при постоянной скорости возрастания амплитуды напряжений. Увеличение напряжений обычно принимают ступенчатым.

Для каждого испытанного образца подсчитывают величину накопленного повреждения

(3.14)

на основании трех условных (предполагаемых) кривых усталости а, б и в (рис. 3.3), охватывающих возможную область рассеяния усталостных характеристик материала.

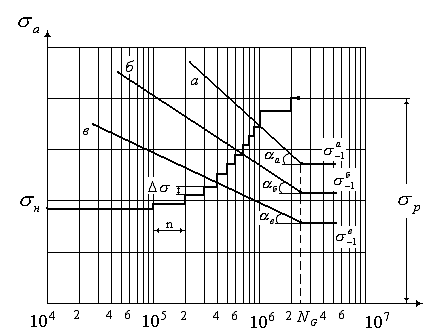
Рис. 3.3. Условные кривые усталости для вычисления предельной суммы накопленных повреждений (3.14)

Далее строят график зависимости суммы накопленных повреждений (3.14), соответствующих данным кривым усталости, от принятого значения предела выносливости (рис. 3.4). По этому графику определяют искомое значение предела выносливости как значение абсциссы, соответствующей ординате, равной единице, то есть для.

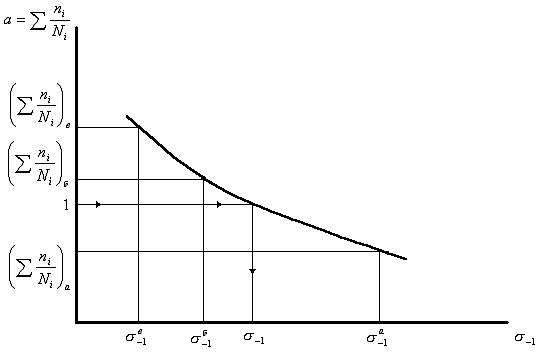
Рис. 3.4. График для определения предела выносливости ускоренным методом Локати

Опыт использования ускоренного метода Локати позволил сформулировать рекомендации по выбору режимов испытания и параметров условных кривых усталости [20].

Принимают скорость возрастания амплитуды напряжения МПа/цикл. Длительность испытания на каждом из уровней напряжений выбирают в диапазоне n=5·10⁴...10⁵ циклов. При этом число ступеней нагружения должно быть не менее 8-10. В противном случае следует снизить длительность испытаний n. Приращение амплитуды напряжения зависит от принятых значений и n и должно находиться в интервале от 5 МПа до 15% значения ожидаемого предела выносливости . Уровень начального напряжения принимают равным ожидаемому значению предела выносливости .

При построении условных кривых усталости долговечность N_G, соответствующую точке перелома, выбирают в диапазоне циклов. Как показывает анализ опытных данных, изменение N_G от 10⁶ до циклов не оказывает существенного влияния на результат ускоренного определения предела выносливости. Дисперсионный и регрессионный анализы показали, что абсолютные размеры образцов и степень концентрации напряжений практически не влияют на абсциссу точки перелома кривой усталости для углеродистых сталей [9].

Абсолютное значение тангенса угла наклона левой ветви кривой усталости (рис. 1.5) для образцов из углеродистых сталей при переменном изгибе можно определить по корреляционному уравнению через предел прочности стали при статическом растяжении [9]

(3.15)

Для крайних условных кривых усталости характеристику наклона левой ветви устанавливают на основании соотношений [20]

(3.16)

(3.17)

При наличии априори достоверных данных относительно значения угла наклона левой ветви кривой усталости принимают

(3.18)

Ожидаемое значение предела выносливости для гладких стальных лабораторных образцов при изгибе с вращением целесообразно определять по корреляционному уравнению (2.10)

Значения пределов выносливости и , соответствующие крайним условным кривым усталости, принимают на 10-15% соответственно выше и ниже ожидаемого предела выносливости .

После определения описанным методом предела выносливости для каждого образца проводят осреднение результатов, то есть

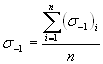(3.19)

где n — число испытанных образцов.

Величина является оценкой предела выносливости исследуемого элемента конструкции. В связи со значительным рассеиванием значений величин испытаниям следует подвергать не менее трех элементов. Увеличение числа образцов (>5) не приводит к заметному снижению погрешности в оценке предела выносливости, которая в основном не превышает 8%. Машинное время при использовании метода Локати сокращается в 10-15 раз в зависимости от объема серии испытаний. Повысить точность оценки предела выносливости ускоренным методом Локати можно уточнением предельной суммы накопленных повреждений (3.14) исследуемого материала при ступенчато возрастающем спектре переменных напряжений.

Следует отметить, что дисперсия величины , получаемая по результатам испытаний серии одинаковых образцов методом Локати, не может служить оценкой меры рассеяния предела выносливости, связанного с неоднородностью свойств материала, состоянием поверхности и т.д., так как разброс результатов ускоренных испытаний по методу Локати в значительной мере обусловлен ошибками в выборе формы и параметров условных кривых усталости.

3.4. Оценка параметров уравнения кривой усталости по результатам форсированных испытаний

Форсирование может осуществляться применением высокочастотных испытательных установок, а также путем испытаний образцов и элементов конструкций при напряжениях, существенно превышающих предел выносливости.

Применение высокочастотных испытательных установок (с частотой 1000 Гц и более) ограничено, так как в процессе испытаний на указанных частотах происходит интенсивный разогрев образцов, в связи с чем возникает необходимость их охлаждения, что искажает результаты испытаний. Кроме этого, рассматриваемый метод форсирования испытаний оказывается малопригодным для образцов с концентратором напряжений и образцов больших сечений. В первом случае — из-за локального разогрева материала в зоне концентратора, во втором — из-за чрезмерного возрастания мощности испытательных установок и наличия заметного градиента температуры по сечению элемента.

Известно, что основное машинное время затрачивается на испытания образцов или элементов конструкций при напряжении, равном или меньшем предела выносливости. Длительность испытаний можно значительно сократить, если ограничиться испытаниями образцов или элементов конструкций лишь при напряжениях, больших предела выносливости, а величину предела выносливости определять путем экстраполяции с помощью уравнения кривой усталости, параметры которого могут быть определены на основании испытаний при высоких уровнях напряжений. В этом заключается суть форсированных испытаний на усталость.

Следует иметь в виду, что приемлемая точность оценки предела выносливости форсированным методом испытания на усталость достигается в случае экстраполяции кривой усталости не более чем на один — два порядка по долговечности, а также при использовании достаточно обоснованных уравнений кривых усталости. Графическая же экстраполяция кривой усталости на один порядок по долговечности приводит к неприемлемой величине ошибки оценки предела выносливости.

Форсированный метод может быть использован для определения как характеристик сопротивления образованию трещины усталости, так и характеристик сопротивления усталостному разрушению.

Применительно к высокопрочным углеродистым и легированным сталям, а также для титановых сплавов, в качестве уравнения кривой усталости следует использовать уравнение Штромейера (1.3), которое в данном случае целесообразно представить в виде

(3.20)

или

(3.21)

где , , a=C, b=-d.

Параметры a и b уравнения (3.21) определяют методом наименьших квадратов по формулам (3.6)- (3.11), в которых m представляет собой число уровней напряжения при испытании на усталость, а n_i – число образцов, испытанных на i-ом уровне напряжения. Оценку указанных параметров производят методом последовательных приближений. Для этого задаются рядом значений и для каждого значения оценивают параметры a и b, а также меру рассеяния Q экспериментальных точек вокруг линии (3.21) по формуле (3.12).

В качестве окончательной оценки параметра уравнения (3.20), представляющего собой предел неограниченной выносливости, принимают величину, которой соответствует минимальное значение Q. Для этого значения окончательно оценивают значения параметров уравнения (3.21). Схема оценки параметра показана на рис. 3.5.

Вычисление предела ограниченной выносливости для выбранной базы производится по формуле (1.3) на основании найденных значений параметров C, d и .

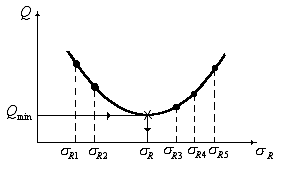
Рис. 3.5. Схема оценки параметра уравнения кривой усталости (3.20)

Точность метода тем выше, чем ближе нижний уровень напряжений при испытании к пределу ограниченной выносливости. Не рекомендуется экстраполяция опытных данных более чем на один — два порядка по долговечности. При выполнении этих условий погрешность метода составляет около 10% при десятикратном сокращении времени испытаний. Экономия в образцах практически отсутствует.

Для алюминиевых, магниевых и титановых сплавов в качестве уравнения кривой усталости принимают уравнение М.Н.Степнова (1.6) при N₁=0. Для случая форсированных испытаний на усталость это уравнение целесообразно представить в виде

(3.22)

или

(3.23)

которое приводят к линейному

(3.24)

где, , , .

Оценку параметров уравнений (3.23) и (3.24) производят методом последовательных приближений. Для этого задаются рядом значений , по формулам (3.6) - (3.11) вычисляют значения параметров уравнения (3.24), и по формуле (3.12) определяют меру рассеяния Q экспериментальных точек вокруг линии (3.24).

В качестве оценки параметра уравнения (3.23) принимают величину, которой соответствует минимальное значение Q. Для полученной величины окончательно по формулам (3.6)- (3.11) вычисляют значения параметров уравнения (3.24), а затем и значения параметров уравнения кривой усталости (3.22) и (3.23).

Схема оценки параметра показана на рис. 3.6.

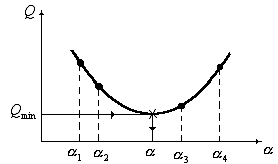
Рис. 3.6. Схема оценки параметра уравнения кривой усталости (3.22) и (3.23)

Экстраполяция кривой усталости при числе испытанных образцов n = 8-10 на два порядка (от N=10⁶циклов до N=10⁸циклов) приводит к относительной средней квадратической ошибке, не превышающей 5-6%.

Этот подход был успешно апробирован и для натурных конструкций из деформируемых алюминиевых сплавов (бурильные трубы, лонжерон несущего винта вертолета, лонжерон хвостового винта вертолета, винт самолета и др.).

3.5. Оценка параметров уравнения кривой усталости по результатам испытаний с возрастающей амплитудой цикла напряжений

Евстратовой С.П. [22] была показана возможность использования ускоренного метода испытания на усталость с возрастающей амплитудой цикла напряжений для оценки параметров уравнения кривой усталости Штромейера (1.3) и М.Н.Степнова (1.6).

Пусть скорость возрастания амплитуды цикла напряжений

(3.25)

Разрушение наступает при амплитуде напряжения и числе циклов n_p в момент, когда сумма накопленных повреждений достигает своего предельного значения

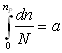(3.26)

Применительно к сталям и титановым сплавам с использованием уравнения Штромейера (1.3) в виде

(3.27)

будем иметь

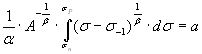(3.28)

где — начальная амплитуда напряжений.

Если принять, предельную сумму независимой от скорости возрастания амплитуды цикла напряжения (что подтверждается результатами испытаний углеродистых и легированных сталей, высокопрочного чугуна и деформируемых алюминиевых сплавов), то уравнение (3.28) можно использовать для определения параметров кривой усталости A, и . Для этой цели следует испытать три группы объектов при различных скоростях нагружения и по полученным значениям амплитуды разрушающих напряжений составить три уравнения по формуле (3.28). Четвертую группу образцов следует испытать при постоянном уровне амплитуды цикла напряжений.

Для деформируемых титановых, алюминиевых и магниевых сплавов с использованием уравнения кривой усталости М.Н.Степнова (1.6) в виде

(3.29)

и с учетом формул (3.25) и (3.26) получим

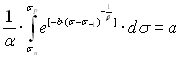, (3.30)

где.

Опыт использования указанной методики позволяет сформулировать последовательность определения параметров уравнения кривой усталости.

Вначале из системы уравнений типа (3.28) и (3.30) определяют параметры и . Далее по результатам усталостных испытаний нескольких образцов на высоком уровне амплитуды напряжения на основании уравнений кривой усталости (3.27) и (3.29) находят параметр A. При необходимости оценку предельной суммы накопленных повреждений можно произвести для найденных значений параметров A, и по уравнениям (3.28) и (3.30).

Точность определения параметров уравнений кривой усталости практически соответствует точности, получаемой при обычных усталостных испытаниях такого же количества образцов, а время испытаний сокращается приблизительно в 10 раз.

Объем и время испытаний дополнительно сокращается на 20-30%, если для исследуемого объекта уже известна предельная сумма накопленных повреждений, которую можно определить, анализируя результаты ускоренных испытаний аналогичных материалов и элементов конструкций.

Рассмотренная методика позволяет производить оценку параметров уравнения кривых усталости как по окончательному разрушению, так и по образованию макротрещины усталости заданной протяженности. В последнем случае в уравнениях (3.28) и (3.30) в качестве принимается амплитуда напряжения, соответствующая появлению макротрещины усталости заданного размера.

4. Оценка характеристик рассеяния усталостных свойств на основании результатов испытаний на усталость форсированным и ускоренным методами

Отсутствие корреляционных связей между числовыми характеристиками рассеяния статических и усталостных свойств конструкционных материалов, а также большая трудоемкость их экспериментальной оценки путем стандартных испытаний на усталость, определяет необходимость разработки и применения форсированных и ускоренных методов испытаний на усталость с целью оценки характеристик рассеяния усталостных свойств материалов и элементов конструкций.

Применительно к числовым характеристикам рассеяния усталостных свойств материалов и элементов конструкций приняты следующие обозначения [4]:

X — случайная величина ( или );

— математическое ожидание случайной величины X (или );

— дисперсия случайной величины X (или );

— среднее квадратическое отклонение случайной величины X (или ),

(4.1)

— коэффициент вариации случайной величины X (или ),

(4.2)

Эмпирические оценки указанных характеристик рассеяния обозначаются теми же буквами с галочкой наверху (,,,) или специальными буквами (,,,соответственно). Часто нижний индекс в обозначении числовой характеристики рассеяния отбрасывают, если он очевиден из условий рассматриваемой задачи (,,, или , , , и т.д.).

4.1. Некоторые эмпирические закономерности рассеяния характеристик усталости

В ходе многих исследований было установлено, что рассеяние долговечности увеличивается с уменьшением уровня амплитуды напряжения при испытании и с увеличением средней долговечности образцов как из черных, так и из цветных сплавов. На рис. 4.1 и 4.2 показаны эти зависимости для конструкционных алюминиевых сплавов АД33, АВ, Д16 и В95 различных плавок. Каждая точка была построена по результатам испытаний на усталость при изгибе с вращением десятков и сотен гладких образцов [1].

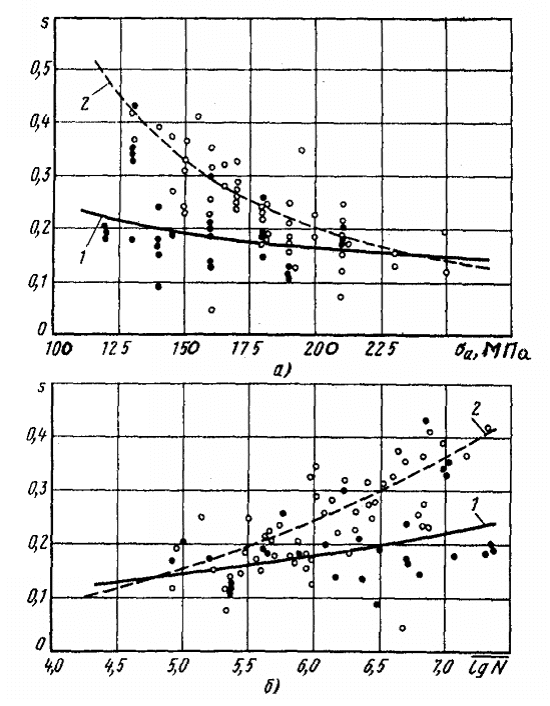
Рис. 4.1. Зависимость среднего квадратического отклонения логарифма долговечности от уровня амплитуды цикла напряжений и среднего значения логарифма числа циклов до разрушения образцов: 1 — сплав АД33, 2 — сплав АВ

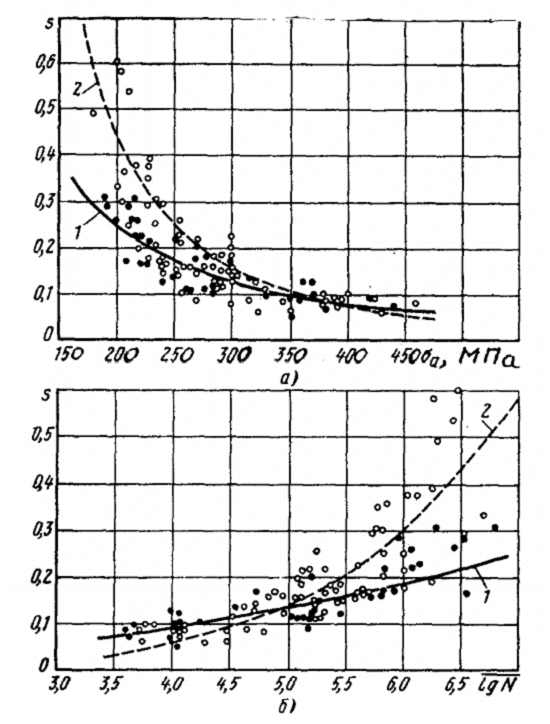
Рис. 4.2. Зависимость среднего квадратического отклонения логарифма долговечности от уровня амплитуды цикла напряжений и среднего значения логарифма числа циклов до разрушения образцов: 1-сплав Д16, 2- сплав В95.

Корреляционный анализ приведенных выше и многих других результатов испытаний на усталость позволяет считать в первом приближении, что между средним квадратическим отклонением логарифма числа циклов до разрушения и уровнем амплитуды цикла напряжений и средним значением логарифма долговечности существует степенная зависимость в виде

(4.3)

и

(4.4)

где — амплитуда цикла напряжений при испытании, b₁, , b₂, и — параметры уравнений (4.3) и (4.4).

Подтверждением этого служит таблица 4.1, где наряду со значениями параметров уравнений (4.3) и (4.4) для деформируемых алюминиевых сплавов АД33, АВ, Д16 и В95 приведены значения эмпирического коэффициента корреляции r между величинами и , и , а также средней квадратической ошибки коэффициента корреляции S_r [1]. Для всех рассмотренных случаев абсолютное значение коэффициента корреляции, как следует из таблицы 4.1, существенно выше своей среднеквадратической ошибки, что свидетельствует о достаточно тесной линейной зависимости между случайными величинами y и x₁, y и x₂, т.е. о существовании соотношений (4.3) и (4.4).

Для указанных выше алюминиевых сплавов графики уравнений (4.3) и (4.4) приведены на рис. 4.1 и 4.2.

Таблица 4.1. Значения параметров уравнений (4.3) и (4.4)

сплав	число исследованных вариантов плавок и размеров профилей	число уровней амплитуд напряжений	число испытанных образцов	уравнение (4.3)				уравнение (4.4)
				b1		r1		b2		r2
АД33	7	30	411	2,79	-0,535	-0,51	0,13		1,244	0,45	0,14
АВ	44	109	3480		-1,719	-0,68	0,07		2,509	0,67	0,08
Д16	13	38	805		-1,645	-0,75	0,07		1,881	0,67	0,09
В95	25	66	1838		-2,625	-0,94	0,01		4,220	0,69	0,06

Существование зависимостей (4.3) и (4.4) наиболее надежно подтверждает корреляционный анализ результатов испытаний на усталость большой партии образцов (n = 1590) из сплава АВ одной плавки [1] (таблица 4.2).

Таблица 4.2. Корреляционный анализ результатов испытаний на усталость образцов из сплава АВ одной плавки

уравнение (4.3)				уравнение (4.4)
569	-1,473	-0,93	0,05		2,944	0,99	0,01

Абсолютное значение эмпирического коэффициента корреляции в этом случае достигает величины 0,93-0,99, а его средняя квадратическая ошибка не превышает 0,05, что говорит о тесной связи среднего квадратического отклонения логарифма долговечности с уровнем амплитуды цикла напряжений и средним значением величины .

Характеристики рассеяния предела ограниченной выносливости этой серии образцов из сплава АВ приведены в таблице 4.3.

Таблица 4.3. Характеристики рассеяния пределов ограниченной выносливости образцов из сплава АВ

Характеристика рассеяния	База испытаний в циклах
		10^6		10^7		10^8
, МПа	195,1	176,5	144,9	135,5	118,4	113,8
, МПа	18,2	15,9	12,5	10,7	9,4	8,9
	0,093	0,090	0,086	0,079	0,079	0,078

Среднее квадратическое отклонение предела выносливости для базы N=5×10⁵ циклов составляет 18,2 МПа, а для базы N=10⁸ циклов — 8,9 МПа (таблица 4.3), т. е. снижается почти в два раза, в то время как коэффициент вариации предела выносливости практически остается на одном уровне (=8-9 %).

Следует отметить, что коэффициент вариации пределов ограниченной выносливости существенно выше, чем коэффициент вариации предела прочности, который у рассматриваемого сплава составляет 0,01-0,03.

Корреляционный анализ полученных результатов (таблица 4.3) дает основание считать, что между средним квадратическим отклонением предела выносливости и базой испытания существует зависимость в виде

(4.5)

где - база испытаний.

Значения параметров b и для исследованного сплава равны соответственно 73,3 и -2,14. Коэффициент корреляции между величинами и составляет 0,99 при средней квадратической ошибке 0,01, что подтверждает существование степенной зависимости типа (4.5).

При решении практических задач, связанных с оценкой долговечности элементов конструкций, эффективности новых технологий и т. д., из всех ранее перечисленных характеристик рассеяния усталостных свойств наиболее широкое применение получило среднее квадратическое отклонение логарифма числа циклов до разрушения . Однако, как уже было показано, величина в значительной степени зависит от уровня амплитуды цикла напряжений при испытании на усталость и от средней долговечности . Поэтому для надежного обоснования указанных зависимостей требуются испытания на усталость большого объема образцов.

Существенно более стабильной характеристикой рассеяния усталостных свойств для различных участков кривой усталости, как показывает анализ результатов массовых испытаний на усталость, является коэффициент вариации предела ограниченной выносливости. Как видно из данных таблицы 4.3, а также из рис. 4.3, где представлены результаты испытаний образцов различных размеров и с разной степенью концентрации напряжений для широкого круга литейных и деформируемых сплавов на алюминиевой и магниевой основах, коэффициент вариации предела ограниченной выносливости практически не зависит от базы испытаний. Корреляционный анализ указанных результатов показал, что эмпирический (выборочный) коэффициент корреляции между коэффициентом вариации предела ограниченной выносливости и базой испытаний составляет лишь величину r = -0.10, которая соизмерима с его средней квадратической ошибкой S_r = 0.07.

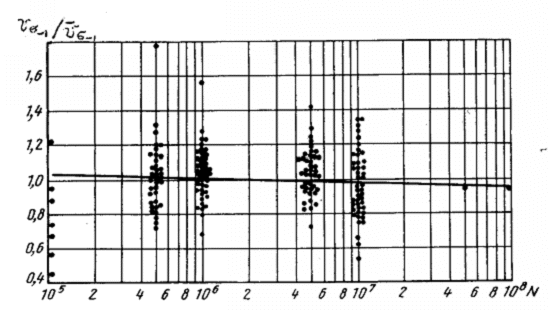
Рис. 4.3. Значения отношений выборочного коэффициента вариации предела ограниченной выносливости для заданной базы к среднему значению коэффициента вариации для каждого сплава, его состояния и геометрии усталостных образцов.

Независимость коэффициента вариации предела ограниченной выносливости от базы испытаний, как это вытекает из теории вероятностей, равнозначна постоянству среднего квадратического отклонения величины для различных базовых долговечностей, что находится в достаточно удовлетворительном соответствии с результатами опытов. Анализ опытных данных показал, что выборочное среднее квадратическое отклонение величины для гладких и надрезанных образцов различных размеров из алюминиевых и магниевых конструкционных сплавов на базе 10⁶ циклов в 24 из 45 случаев несколько больше, чем на базе 10⁷ циклов, и в 21 случае указанная характеристика оказалась несколько меньше на базе 10⁶ циклов, чем на базе 10⁷ циклов.

4.2. Оценка коэффициента вариации предела выносливости по результатам испытаний на высоких уровнях амплитуды цикла напряжений

Принятие гипотезы о независимости коэффициента вариации предела ограниченной выносливости от базы испытаний на усталость создает возможность построения квантильных кривых усталости, если уже надежно построена медианная (средняя) кривая усталости и произведена оценка коэффициента вариации . В этом случае будем иметь

, (4.6)

где - квантиль уровня P предельной амплитуды цикла напряжений для заданной долговечности, - среднее или медианное значение предела выносливости (предельной амплитуды) для заданной долговечности, определяется по медианной кривой усталости (P=0.5), - эмпирическое значение коэффициента вариации предела выносливости, z_p — квантиль уровня P нормального распределения.

Надежная оценка коэффициента вариации предела выносливости на основании стандартных испытаний на усталость требует испытаний большого числа образцов (n = 60...100), что не всегда выполнимо.

Однако, коэффициент вариации предела выносливости можно оценить на основании результатов испытания на усталость форсированным методом. Для этого на высоком уровне амплитуды цикла напряжений подвергают испытаниям n = 15...25 образцов и по полученным результатам оценивают выборочную дисперсию величины по формуле

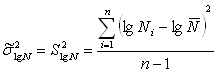. (4.7)

На основании теоремы о числовых характеристиках функции Y случайного аргумента x

(4.8)

математическое ожидание функции равно

(4.9)

где a_x — математическое ожидание случайного аргумента .

Дисперсия функции определяется как

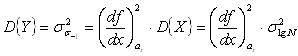(4.10)

Применительно к уравнению кривой усталости Штромейера (1.3) (стали, титановые сплавы), которое для рассматриваемого случая записывают в виде

(4.11)

с учетом (4.2) и (4.10) получают

(4.12)

или

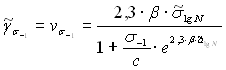(4.13)

Для деформируемых алюминиевых, титановых и магниевых сплавов с использованием уравнения кривой усталости СтепноваМ.Н. [1] в виде (3.22) и формул (4.2) и (4.10) получают оценки коэффициента вариации предела выносливости

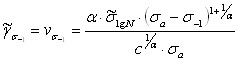(4.14)

или

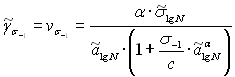(4.15)

Машинное время при форсированных испытаниях на усталость с целью оценки коэффициента вариации предела выносливости при удовлетворительной точности сокращается, примерно, в 100 раз, а число испытанных образцов – в 4 раза по сравнению со стандартными испытаниями на усталость.

Если по результатам испытаний на нескольких уровнях амплитуды цикла напряжений оценены соответствующие значения выборочного коэффициента вариации предела выносливости по формулам (4.12), (4.13) или (4.14), (4.15), то их объединяют в общую оценку

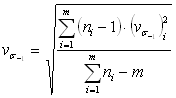(4.16)

где — оценка коэффициента вариации предела выносливости, найденная по результатам испытаний образцов на i-м уровне амплитуды цикла напряжений (i = 1, 2, ..., m).

Принятие гипотезы о независимости коэффициента вариации предела выносливости от базы испытаний наряду с принятым видом уравнения кривой усталости дает возможность выразить зависимость степени рассеяния долговечности от уровня амплитуды цикла напряжений и средней долговечности на всем протяжении кривой усталости.

Применительно к кривой усталости Штромейера (4.11)

(4.17)

и

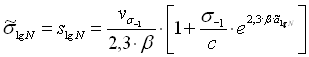(4.18)

При использовании уравнения кривой усталости Степнова М.Н. (3.22) получают

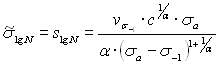(4.19)

и

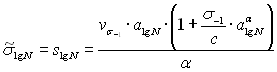(4.20)

Теоретически обоснованные уравнения (4.17)...(4.20) носят более общий характер по сравнению с эмпирически обоснованными уравнениями (4.3) и (4.4).

Зависимости (4.17)...(4.20) подвергались экспериментальной проверке для алюминиевых сплавов различных марок (АД33, АВ, Д16, В95 и др.). Для всех рассмотренных случаев соответствие указанных уравнений опытным данным вполне удовлетворительное. Несколько лучшее соответствие имеют уравнения (4.19) и (4.20), дающие близкие результаты с уравнениями (4.3) и (4.4).

4.3. Ускоренный метод оценки дисперсии предела выносливости

Другую возможность оценки характеристик рассеяния усталостных свойств материалов и элементов конструкций дают результаты испытаний на усталость с возрастающей амплитудой цикла напряжений. Для этой цели при постоянной скорости возрастания амплитуды испытывают серию из n образцов и вычисляют выборочное значение среднего и дисперсию разрушающей амплитуды цикла напряжений по формулам

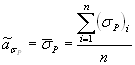(4.21)

и

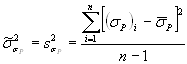(4.22)

Проведенный автором [1, 25] статистический анализ результатов массовых испытаний на усталость литейных и деформируемых магниевых и алюминиевых сплавов (таблица 4.4) показал, что дисперсия разрушающих амплитуд не зависит скорости нагружения.

Уровни значимости критерия Бартлета [4] о равенстве генеральных дисперсий разрушающих амплитуд для всех рассмотренных скоростей нагружения не опускаются ниже . Впоследствии эта закономерность была подтверждена [21] и для сплавов на железной основе.

Уровень начального значения амплитуды цикла напряжения также не оказывает заметного влияния на дисперсию разрушающих напряжений. Так, применение критерия Фишера [4] о равенстве генеральных дисперсий разрушающих амплитуд цикла напряжений для двух значений уровней начальной амплитуды (таблица 4.4) показывает, что отношение выборочных дисперсий незначимо отличается от единицы. Например, для сплава АД35 - F = 1.26, в то время как для уровня значимости =0.05 критическое значение критерия ; для сплава типа АВ с 0,6% Mn и 0,01% Cu - F = 1,10 при и для сплава типа АВ с 0.12% Mn и 0.04% Cu - F = 1,02 при .

Независимость дисперсии разрушающих амплитуд цикла напряжений от уровня начальной амплитуды и скорости возрастания напряжений дает возможность оценки обобщенной дисперсии путем объединения дисперсий для различных скоростей и уровней начальной амплитуды

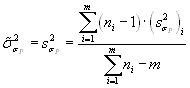, (4.23)

где — дисперсия разрушающих амплитуд цикла напряжений при скорости α_i возрастания амплитуды, подсчитывается по формуле (4.22); m — число вариантов скоростей возрастания амплитуды для всех значений уровней начального напряжения; n_i — число испытанных образцов при скорости α_i.

Анализ и сопоставление результатов обычных испытаний на усталость и испытаний с возрастающей амплитудой цикла напряжений, а также структура уравнения (3.1), дают основания считать, что дисперсия предела выносливости равна дисперсии разрушающих амплитуд цикла напряжений , то есть

(4.24)

Таблица 4.4. Результаты ускоренных испытаний с возрастающей амплитудой цикла напряжений образцов из легких сплавов

Сплав	, МПа	10^4, МПа/цикл	n	, МПа		, (МПа)^2		Обобщенная (осредненная) дисперсия,
				по скорости	по скорости  и уровню начального напряжения
Магниевый сплав МЛ5	33	0,4 2,0 6,0	20 20 15		81,8 99,9 115,5		133,0 143,2 129,3	135,6	135,6
Алюминиевый сплав АД35	0	0,34 0,87 1,70 2,56 3,34 6,68	20 20 20 20 20 10		178,1 194,7 204,0 218,2 227,9 247,6		108,2 41,5 58,2 95.0 129,5 85,0	86,3	90,9
	100	0,34 1,70 3,34	10 10 10		168,1 193,9 211,3		102,1 46,3 169,2	108,6
Алюминиевый сплав типа АВ (Cu – 0,46%, Mn – 0,25%)	100	0,332 1,66 3,32 6,64	25 20 20 10		184,8 217,2 238,5 258,6		115,6 87,5 100,0 144,0	107,9	107,9
Алюминиевый сплав типа АВ (Cu – 0,01%, Mn – 0,6%)	100	0,332 0,87 1,66 3,32 6,64	10 10 10 10 10		172,1 181,1 194,4 210,4 225,4		36,6 40,1 42,3 55,3 55,0	45,4	47,5
	150	0,332 0,87 1,70 3,32 6,64	5 10 5 10 10		161,8 176,1 185,6 208,2 216,7		24,7 53,7 51,1 47,3 60,0	50,1
Алюминиевый сплав типа АВ (Cu – 0,095%, Mn – 0,28%)	100	0,332 0,87 1,70 3,32 6,64	10 10 10 10 10		167,8 180,8 192,3 207,2 225,0		50,0 31,4 35,1 31,8 35,8	36,9	36,9
Алюминиевый сплав типа АВ (Cu – 0,04%, Mn – 0,12%)	100	0,332 1,83 6,64	10 10 10		165,0 194,4 231,8		54,0 65,4 43,8	54,3	54,7
	150	0,332 1,83 6,64	10 10 10		161,2 191,0 227,5		52,1 53,6 59,6	55,1

Условные обозначения:

- начальный уровень амплитуды цикла напряжений; - скорость возрастания амплитуды; n — число испытанных образцов; - выборочное среднее значение амплитуды разрушающих напряжений; - выборочная дисперсия амплитуды разрушающих напряжений; - обобщенная (осредненная) дисперсия амплитуды разрушающих напряжений.

Для легких сплавов эта дисперсия соответствует базе N= 10⁷ циклов. Для других баз испытания дисперсию предела выносливости алюминиевых сплавов с учетом инвариантности его коэффициента вариации к базе и уравнения (2.38) подсчитывают по формуле

, (4.25)

а для титановых сплавов с учетом (2.43)

. (4.26)

Изложенная методика ускоренной оценки дисперсии предела выносливости и рассмотренный ранее способ расчета медианы или среднего значения предела выносливости позволяют оценить коэффициент вариации этой характеристики сопротивления усталости

, (4.27)

который (на основании уравнений (4.17) ...(4.20)) открывает возможность расчета среднего квадратического отклонения логарифма долговечности на любом участке кривой усталости.

Представление о точности оценки характеристик рассеяния усталостных свойств на основании результатов ускоренных испытаний с возрастающей амплитудой цикла напряжений дает таблица 4.5, где сопоставлены итоги использования ускоренного и обычного методов испытаний на усталость для литейного магниевого сплава МЛ5 и деформируемого алюминиевого сплава АВ.

Таблица 4.5. Сопоставление характеристик рассеяния предела выносливости образцов из легких сплавов МЛ5 и АВ, определенных по результатам ускоренного и обычного методов испытаний

Характеристика	Метод определения	Сплав АВ			Сплав МЛ5
		N=10^7	N=5	N=10^8	N=10^7
Медиана предела выносливости в МПа	Ускоренный	141	124	120	63
	Обычный	135	119	113	67
	Расхождение в %	+4,4	+4,2	+6,2	-6,0
Среднее квадратическое отклонение предела выносливости в МПа	Ускоренный	10,4	9,2	8,8	11,6
	Обычный	10,7	9,4	8,9	10,5
	Расхождение в %	-2,8	-2,1	-1,1	+10,5
Коэффициент вариации предела выносливости	Ускоренный	0,074	0,074	0,073	0,184
	Обычный	0,079	0,079	0,079	0,157
	Расхождение в %	-6,3	-6,3	-7,6	+17,2

Анализ результатов, приведенных в таблице 4.5, показал, что рассмотренная методика ускоренной оценки дисперсии предела выносливости дает вполне удовлетворительные результаты. Аналогичные результаты были получены и для других сплавов, а также для натурных элементов конструкций [20].

Вопросам планирования испытаний на усталость, в том числе и ускоренных, посвящены работы Агамирова Л.В. [23, 26, 27 и др.], в которых даны оценки погрешностей определения усталостных характеристик в зависимости от объема и методики испытаний. Применительно к испытаниям, рассмотренным в настоящем разделе, показано, что относительная средняя квадратическая ошибка оценки среднего квадратического отклонения предела выносливости в долях этого отклонения определяется из приближенного асимптотического уравнения

, (4.28)

которое может быть использовано для определения необходимого объема ускоренных испытаний на усталость с целью оценки среднего квадратического отклонения предела выносливости с погрешностью, не превышающей , то есть

. (4.29)

4.4. Построение кривой распределения предела выносливости по результатам испытаний на усталость с возрастающей амплитудой цикла напряжений

Анализ кривых распределения разрушающих амплитуд цикла напряжений, приведенных в качестве примера на рис. 4.4 для сплавов АВ и МЛ5 (для других легких сплавов и сталей они имеют аналогичный вид), показал, для каждого материала и типа образцов при различных скоростях возрастания амплитуды цикла напряжений форма и наклон кривых распределения одинаковы, а различаются лишь медианные значения разрушающих амплитуд. Это позволяет по результатам ускоренных испытаний оценивать не только медиану предела выносливости и его дисперсию, но и производить оценку квантильных значений предела выносливости и строить эмпирическую функцию распределения [1].

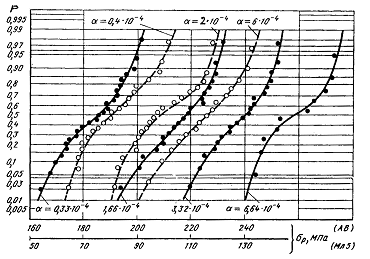
Рис. 4.4 Кривые эмпирических распределений разрушающих амплитуд напряжений для алюминиевого сплава АВ (сплошные линии, верхняя шкала ) и магниевого сплава МЛ5 (штриховые линии, нижняя шкала ).

Для этого все результаты ускоренных испытаний для рассматриваемого материала и типа образцов (m выборок) объединяют в одну общую совокупность путем введения случайной величины — отклонения от медианы

, (4.30)

где - оценка медианы разрушающей амплитуды цикла напряжений при i-ой скорости нагружения; - j-й член вариационного ряда разрушающей амплитуды цикла напряжений при i-ой скорости нагружения.

Далее строят общий вариационный ряд из значений x_ij и наносят на нормальной вероятностной сетке график эмпирической функции распределения величины x_ij. Подобные обобщенные кривые распределения для ряда сплавов приведены на рис. 4.5.

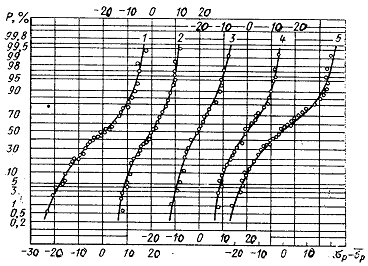
Рис. 4.5 Обобщенные кривые распределения отклонений разрушающих амплитуд цикла напряжений от среднего значения:
1. — Сплав АВ (Cu – 0,46%, Mn – 0,25%), n=75;
2. — Сплав типа АВ (Cu – 0,010%, Mn – 0,60%), n=90;
3. — Сплав типа АВ (Cu – 0,095%, Mn – 0,28%), n=50;
4. — Сплав типа АВ (Cu – 0,04%, Mn – 0,12%), n=60;
5. — Сплав МЛ5, n=55.

Характер кривых распределения разрушающих амплитуд цикла напряжений (см. рис. 4.4) и отклонений от медианы (см. рис. 4.5) свидетельствует о существовании нижней и верхней границ разрушающих амплитуд. Преобразование распределения путем введения нижней границы разрушающих амплитуд и верхней границы приводит распределение случайной величины к нормальному (рис. 4.6).

Значение нижней границы зависит от скорости возрастания амплитуды напряжений, однако разность так же, как и , для каждого сплава является устойчивой величиной, не зависящей от скорости возрастания амплитуды и уровня начального напряжения.

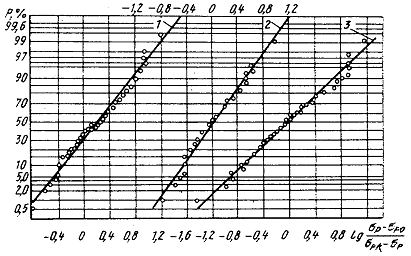
Рис. 4.6 Преобразование распределения путем введения верхней и нижней границ разрушающих напряжений:
1. — Сплав АВ (Cu – 0,46%, Mn – 0,25%), =30МПа, =20МПа;
2. — Сплав типа АВ (Cu – 0,095%, Mn – 0,28%), =15МПа, =15МПа;
3. — Сплав МЛ5, =22МПа, =23МПа.

Квантили предела выносливости для уровня вероятности P находят из выражения

, (4.31)

где x_p — оценка квантиля величины x_ij, определяемая по графику эмпирической функции распределения (рис. 4.5); - оценка медианы предела выносливости, определяемая по формуле (3.1).

Произведя вычисления по формуле (4.31) для нескольких уровней вероятности P, строят эмпирическую функцию распределения предела выносливости. Расчет значений предела выносливости образцов из алюминиевых и титановых сплавов для базы, отличной от 10⁷ циклов, производят с помощью уравнений соответственно (2.38) и (2.43).

На рис. 4.7в качестве примера сопоставлены эмпирические кривые распределения пределов ограниченной выносливости сплавов АВ и МЛ5, построенные по результатам обычных и ускоренных испытаний. Приведенные данные показывают удовлетворительное соответствие характеристик сопротивления усталости, найденных указанными методами. Расхождения в пределах выносливости не превышают 5.8МПа. Аналогичные результаты имеют место и для других марок алюминиевых сплавов, а также для углеродистой и легированной сталей.

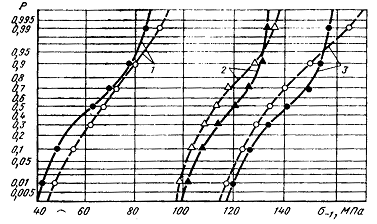
Рис. 4.7 Сопоставление кривых эмпирических распределений пределов ограниченной выносливости, найденных ускоренным (сплошные линии) и обычным (штриховые линии) методами
1. — Сплав МЛ5, N_б=10⁷ циклов;
2. — Сплав АВ, N_б=10⁸ циклов;
3. — Сплав АВ, N_б=10⁷ циклов.

Как уже отмечалось, при использовании метода Про для оценки медианы предела выносливости требуется такое же число образцов, как и при обычных испытаниях. Однако, при построении кривой распределения предела выносливости ускоренным методом с возрастающей амплитудой цикла напряжений в связи с возможностью объединения отдельных выборок в единую совокупность для сплавов со стабильными усталостными свойствами число объектов должно составлять лишь 30 - 40, а для сплавов с повышенной дисперсией усталостных свойств 40 - 60 штук. Случайная ошибка оценки квантили предела выносливости для малых уровней вероятностей будет такой же, как и при обычном методе испытаний 100 - 150 образцов. Таким образом, при построении кривой распределения предела выносливости наряду с 10 - 50-кратным сокращением машинного времени достигается двух-трехкратная экономия объектов испытаний.

Рассмотренная выше методика позволяет производить оценку характеристик рассеяния усталостных свойств как по окончательному разрушению, так и по образованию макротрещины усталости определенного размера.

Список литературы

1. Степнов М.Н., Гиацинтов Е.В. Усталость легких конструкционных сплавов. М.: Машиностроение, 1973. 318 с.

2. Степнов М.Н., Ковалев И.Е., Николаев А.В., Виссарионов И.С., Александрова Т.С. Уравнения кривых усталости титановых сплавов и расчетный метод их построения. «Заводская лаборатория», 1999, №12, с. 31-39.

3. Хэйвуд Р.Б. Проектирование с учетом усталости / пер. с англ. Под ред. И.Ф.Образцова. М.: Машиностроение. 1969. 504 с.

4. Степнов М.Н. Статистические методы обработки результатов механических испытаний. М.: Машиностроение. 1985. 231 с.

5. Степнов М.Н., ЕвстратоваС.П., Борисова В.В. Косвенная оценка пределов выносливости сталей и алюминиевых сплавов. «Заводская лаборатория», 1981, №3, с. 67-69.

6. Степнов М.Н., Ковалев И.Е., Николаев А.В., Виссарионов И.С., Александрова Т.С. Косвенная оценка пределов выносливости титановых сплавов при переменном изгибе, растяжении-сжатии и кручении. «Заводская лаборатория», 1999, №3, с. 41-44

7. Серенсен С.В., КогаевВ.П., Шнейдерович Р.М. Несущая способность и расчет деталей машин на прочность. М.: Машиностроение. 1975. 488 с.

8. Когаев В.П. Расчеты на прочность при напряжениях, переменных во времени. М.: Машиностроение. 1993. 364с.

9. Гребеник В.М. Усталостная прочность и долговечность металлургического оборудования. М.: Машиностроение. 1969. 256с.

10. Степнов М.Н., Евстратова С.П., Николаев А.В., Александрова Т.С. Расчетно-экспериментальные методы оценки характеристик сопротивления усталости конструкционных и алюминиевых сплавов при асимметричном нагружении. «Проблемы машиностроения и надежности машин», РАН, 1998, №2, с. 117-122

11. Степнов М.Н. Расчетно-экспериментальный метод построения диаграмм предельных амплитуд для конструкционных деформируемых алюминиевых сплавов с учетом концентрации напряжений. «Вестник машиностроения», 1998, №9, с. 11-17

12. Степнов М.Н., Николаев А.В., Веселова О.Н., Шибанова И.С. Расчетно-экспериментальные методы оценки характеристик сопротивления усталости конструкционных алюминиевых сплавов при осевом нагружении. «Заводская лаборатория», 1998, №7, с.38-40.

13. HowellF.M. and Miller J.L. Axial-stress fatique strengths of several structural aluminium alloys. Proceeding ASTM, vol. 55, 1955. p. p. 955-967.

14. ГОСТ 25.504-82. Расчеты и испытания на прочность. Методы расчета характеристик сопротивления усталости. Издательство стандартов, Москва, 1982, 80с.

15. Степнов М.Н. Чувствительность конструкционных материалов к асимметрии цикла напряжений. «Вестник машиностроения », 1999, №12, с.39-41.

16. Воробьев А.З., Олькин Б.И., Стебнев В.Н., Родченко Т.С. Сопротивление усталости элементов конструкций. М.: Машиностроение, 1990, 239 с.

17. Gunn K. Effect of yielding on the fatique properties of test pieces containing stress concentrations // Aeronautical Quarterly, 1955. 6. Nov. P. 277.

18. Grover H.J., Bishop S.M. & Jackson. Axial load fatique tests on notched sheet specimens of 24S-T3 & 75S-T6aluminium alloys and SAE 4130steel with stress concentration factors of 2and 4. // NACA. Technical Note. 2389. 1951.

19. Сочава А.И. Исследование сопротивления усталостному разрушению легких конструкционных сплавов в условиях асимметрии цикла // Автореф. дис. . канд. техн. наук. МАТИ. М., 1977. 16 с.

20. Степнов М.Н. Ускоренные испытания на усталость. М.: Машиностроение, 1975. 57 с.

21. Балаковский О.Б. Оценка рассеяния пределов выносливости ускоренным методом. В сб. «Ускоренные испытания на надежность технических систем». М.: Издание стандартов, 1974. с. 180-190.

22. Евстратова С.П. Ускоренные методы усталостных испытаний применительно к элементам конструкций из легких сплавов (автореферат диссертации). М.: МАТИ им.К.Э.Циолковского, 1973, 18 с.

23. Агамиров Л.В. Разработка статистических методов оценивания характеристик усталостных свойств материалов и показателей надежности элементов конструкций авиационной техники (автореферат диссертации). М.: МГАТУ, 1994, 40 с.

24. Агамиров Л.В. Расчетное обоснование кривой усталости элементов конструкций на базе критерия подобия усталостного разрушения. «Вестник машиностроения», 2000, №11, с. 27-31.

25. Степнов М.Н., Шухмин Ю.А. Оценка дисперсии усталостных свойств легких сплавов модифицированным методом Про. «Заводская лаборатория», 1967, №9, с. 1118-1122.

26. Степнов М.Н., Агамиров Л.В. Исследование точности определения пределов ограниченной выносливости элементов конструкций из легких сплавов. Известия ВУЗов. Машиностроение, 1981, №8, с. 21-24.

27. Степнов М.Н., Агамиров Л.В. Расчеты и испытания на прочность в машиностроении. Планирование и статистическая обработка результатов статических испытаний на усталость. Методические указания. РД 50-705-91. М.: Издательство стандартов, с. 167.

28. Вентцель Е.С. Теория вероятностей. М.: Наука, 1969, 576 с.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Строительная механика Теория машин и механизмов

00:00:00