Главная
Раздел 7. Приближенные методы
расчета колебаний
Рассмотренные выше методы расчета становятся тем более громоздкими, чем сложнее структура рассчитываемой системы. Поэтому возникает необходимость в способах, позволяющих достаточно просто рассчитывать и сложные системы.
Один из возможных путей состоит в применении простых приближенных формул (например, формулы Рэлея). В этом случае задают форму колебаний системы, сводя её таким образом к системе с одной степенью свободы. При удачной аппроксимации получают достаточно точное значение низшей собственной частоты системы, однако другие её динамические характеристики остаются нераскрытыми.
Cхематизация реальной системы, как имеющей несколько степеней свободы, достигается в методе Рэлея-Ритца, при использовании которого форма колебаний системы задаётся в виде выражения, включающего несколько параметров.
Другим приёмом, позволяющим свести реальную систему к системе с конечным числом степеней свободы, является метод прямой дискредитации. Чем больше число элементов, на которые разбита система при использовании этого метода, тем ближе расчётная схема к исходной системе. Вместе с тем, если элементы выбраны однотипными, то даже при большом их числе оказывается возможным реализовать расчёт колебаний, используя матричные методы с применением ЭВМ. Примерами таких методов являются метод начальных параметров в форме матриц перехода и метод прогонки.
При динамических расчётах конструкций сложной конфигурации также широко используется метод конечных элементов.
В том случае, когда сложную колебательную систему можно разделить на несколько подсистем, динамические характеристики которых определяются сравнительно просто, полезными являются методы динамических податливостей и жёсткостей. Эти методы представляют собой обобщение на динамические задачи метода сил и метода перемещений строительной механики.
В методе последовательных приближений задача об определении собственных частот и форм колебаний сводится к многократному расчёту деформаций системы под действием известной статической нагрузки.
Рассмотрим некоторые из используемых приближённых методов.
7.1. Теорема
и метод Рэлея
Согласно этой теореме, истинное значение низшей собственной частоты всегда меньше, чем приближенное значение частоты, вычисленное энергетическим способом. Докажем эту теорему для изгибных колебаний, совершенно аналогично она доказывается и для других видов колебаний.
Положим, что при решении энергетическим способом задачи о свободных изгибных колебаниях была принята форма колебаний f = f(x). Тогда соответствующая статическая нагрузка, способная вызвать изгиб по кривой f(х), может быть представлена в виде
Следовательно, приближенное выражение для квадрата частоты
.
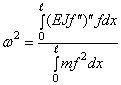(264)
Ввиду известного произвола в выборе функции f(x) она не совпадает ни с одной из собственных форм, которые являются точными решениями; однако функцию f(x) можно представить в виде ряда по этим формам. Если ищут низшую собственную частоту, то функцию f(x) можно представить так:
f(x) = X1(x)+ b2X2(x)+b3X3(x)
+... (265)
При удачном выборе функция f(x) близка к Х1(х), поэтому коэффициенты b2 , b3 ... - малые числа .
Два раза продифференцируем выражение (265) по х, затем умножим обе части на жёсткость EJ и вновь дважды продифференцируем результат. Тогда получим
(266)
Согласно основному уравнению (243), можно записать:
; 
;...
Подставляя эти значения в выражение (266), получим
(267)
При помощи (265) и (267) образуем числитель формулы (264):
.
Вследствие ортогональности собственных форм все интегралы от произведений, где индексы сомножителей различны, равны нулю, поэтому
.
(268)
Знаменатель формулы (264) получим при помощи (265) в виде
(269)
Здесь также исчезают все члены, содержащие произведения Xm Xn. Подставляя (268) и (269) в (264), получим квадрат низшей частоты
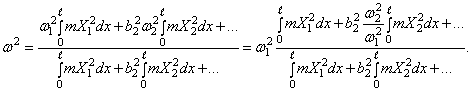(270)
Так как w1<w2<w3<...,
то все дроби 
больше единицы и,
следовательно, все члены числителя, начиная со второго, больше соответствующих
членов знаменателя. Поэтому вся дробь, входящая в (270), больше единицы, т е.
w2>
,
(271)
что и утверждается теоремой Рэлея.
Неравенство (271) справедливо не только для изгибных, но и для продольных и крутильных колебаний.
7.2. Метод
Ритца
Зададимся несколькими функциями f1(x) , f2(x) ,... , fn(x), каждая из которых удовлетворяет геометрическим граничным условиям задачи, и образум функцию f(x) как сумму
f(x) = C1f1(x) +C2f2(x)+...+Cnfn(x). (272)
Если эту функцию подставить в формулу Рэлея
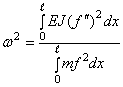, (273)
то результат будет зависеть от конкретного выбора коэффициентов С1 , С2 , …, Сn.
Метод Ритца основан на простой идее: коэффициенты С1 , С2 , …, Сn должны быть выбраны так, чтобы вычисление по (273) дало наименьшее значение для w2. Из теоремы Рэлея вытекает, что такой выбор будет наилучшим (при данной системе функций fi).
Условия минимума w2 имеют вид
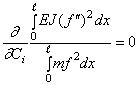, (i =
1 , 2,..., n),
т.е.
.
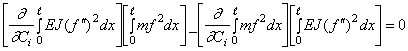Разделив это уравнение на интеграл 
и учитывая
(273), получим
(i =
1 , 2,..., n). (274)
Уравнения (274) однородны и линейны относительно С1 , С2 , …, Сn и их число равно числу членов выражения (272). Приравнивая нулю определитель, составленный из коэффициентов при С1 , С2 , …, Сn, получим частотное уравнение. Это уравнение не только дает хорошее приближение для низшей частоты, но также определяет (хотя и с меньшей точностью) значения высших частот; при этом можно будет вычислить столько частот, сколько слагаемых принято в выражении (272).
Метод Ритца, как и метод Рэлея, позволяет решить задачу в случаях разрывных функций EJ и m и когда эти функции представлены различными аналитическими выражениями на различных участках.
Иногда та же идея используется в иной форме. Например, при исследовании поперечных колебаний турбинных лопаток задаются функцией f(x) = axs (начало координат в закрепленном конце). Применяя затем формулу Рэлея (273), получают частоту в виде зависимости от показателя степени s. Затем при помощи числовых расчетов определяют значение s, которому отвечает наименьшая частота. Это позволяет достаточно надежно определить как форму, так и частоту колебаний первого тона.
Пример 20. Определить методом Ритца низшую собственную частоту поперечных колебаний консоли переменного сечения, имеющей толщину, равную единице; высота изменяется по линейному закону:
; 
; 
(
- длина консоли).
Решение
Точное значение низшей частоты такой консоли вычислено Кирхгофом в виде
.
Для приближенного решения принимаем
Каждый член этого разложения удовлетворяет граничным условиям задачи
, 
при х=.
Если ограничиться одним членом разложения, то по методу Рэлея
,
при этом ошибка составляет около 3 %.
Чтобы получить лучшее приближение, возьмем два члена разложения, подставив их в (274),
.
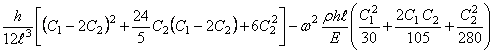Дифференцируя это выражение по С1 и С2 поочередно, приходим к системе уравнений
.
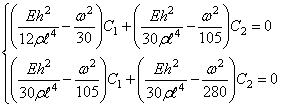Приравнивая нулю определитель, составленный из коэффициентов этих уравнений, получим частотное уравнение, меньший корень которого
,
что даёт ошибку 0,1 %.
7.3. Метод Граммеля
Принимая форму колебаний подобной статическим прогибам системы от некоторой подходящей нагрузки, можно существенно увеличить точность расчёта за счёт исключения операции дифференцирования. Еще большая точность достигается в методе Граммеля, в котором дифференцирование заменяется интегрированием. Последовательность операций здесь такова:
1.
Задают форму колебаний и вычисляют максимальную кинетическую энергию движения:
.
2.
Определяют максимальные силы инерции:
.
3. Определяют внутренние силы в элементах системы, вызываемые нагрузками Fi.
4. По внутренним силам вычисляют максимальную потенциальную энергию деформации П0.
5. Из равенства Кmax = П0 определяют частоту колебаний.
Применим
метод Граммеля для вычисления частоты колебаний
консольной балки. Принимая x
= (z/)2, находим
.
Интенсивность сил инерции:
.
Поперечная сила в сечении:
.
Изгибающий момент:
.
Потенциальная энергия деформации:
.
Приравнивая Kmax = По, находим
,
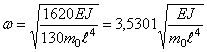что отличается от точного решения на 0,42 %.
7.4. Формула
Донкерлея
Так как метод Рэлея приводит к завышенному значению частоты колебаний, то весьма полезным является применение метода (формулы), дающего заниженное значение низшей частоты колебаний. Простейшей из такого рода формул является формула Донкерлея.
Рассмотрим какую-либо многомассовую систему, например балку (рис.74,а). Пусть на этом рисунке изображена точная форма собственных колебаний системы.
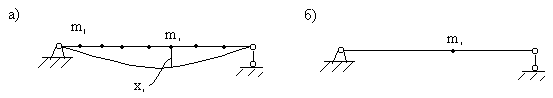
Рис. 74
Тогда точное значение собственной частоты системы выражается формулой
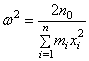. (275)
Теперь рассмотрим ту же балку, но только с одной массой mi (рис.74, б). В этом случае частота колебаний будет определяться по формуле
,
где dii - податливость балки при приложении силы в точке расположения массы mi .
С другой стороны, приближённое значение wi той же частоты можно определить по формуле Рэлея, считая, что форма колебаний совпадает с изображённой на рис.74,а
.
(276)
Здесь По и xi имеют те же значения, что и в (275).
Так как форма, изображённая на рис.74,a, не является точной формой колебаний одномассовой системы, то выполняется неравенство:
.
(277)
Сравнивая (275) и (276), находим
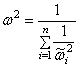. (278)
Eсли в
правой части полученного равенства заменить 
меньшими значениями 
, то равенство превратится в неравенство:
.
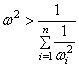Таким образом, приближенная формула Донкерлея всегда дает преуменьшенное значение частоты:
.
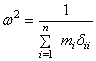(279)
Рассчитав частоту одной и той же системы по методу Рэлея и формуле Донкерлея, получим вилку, в которой заключено истинное значение частоты колебаний.
7.5. Метод
последовательных приближений
Докажем, что обычный процесс последовательных приближений приводит к первой собственной форме колебаний. Основой процесса является сравнение двух кривых аn и аn+1, из которых вторая получается как линия прогибов, вызванных нагрузкой man; при этом приближенное значение квадрата частоты определяется по формуле
.
(280)
Подобно
выражению (265) представим исходную кривую 
в виде ряда
(281)
Тогда
нагрузка, соответствующая прогибам 
, такова:
(282)
Рассмотрим
одно из слагаемых этой нагрузки - 
. От нагрузки 
прогибы будут 
, поэтому от нагрузки прогибы будут в 
раз больше, т.е.
составят 
. Следовательно, кривая прогибов от суммарной нагрузки определяется
рядом
(283)
который
отличается от ряда (282) тем, что каждый член ряда разделен на квадрат
соответствующей частоты. Так как 
то кривая 
ближе к 
, чем исходная кривая ; члены ряда, содержащие 
, 
и искажающие основную
форму , представлены в ряде (283) слабее, чем в ряде (281).
Продолжая процесс дальше, получим для 
кривой
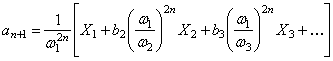. (284)
Как видно, при 
высшие
формы исчезают; следовательно, какой бы ни была выбрана исходная кривая (например,
даже очень похожей на вторую собственную форму), процесс в конечном итоге
приведет именно к первой собственной форме.
Поэтому может показаться, что попытка построить вторую собственную форму при помощи этого метода обречена на неудачу, так как всякое искажение, вносимое первой формой в приближенную вторую форму, будет постепенно увеличиваться; после большого числа построений второй тип колебаний совершенно исчезнет, и останется лишь первый тип.
Однако несколько видоизменяя метод, можно добиться того, что в результате последовательных приближений «очистится» не первая, а именно вторая собственная форма колебаний. Этот прием нашел практическое применение при расчете изгибных колебаний крыльев самолетов и лопаток турбин.
Прием основан
на устранении формы 
из исходной функции . Допустим, что в разложении (281) отсутствует слагаемое,
соответствующее первой форме, тогда оно не сможет возникнуть при всех
последующих операциях, и ряд (284) принимает вид
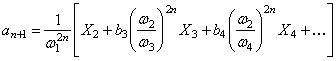
При исчезнут все формы
колебаний, кроме второй. Чтобы процесс последовательных приближений привел
именно ко второй форме, нужно из исходной функции исключить первую
собственную форму . Это можно сделать, приняв в качестве основы для построения
второго приближения функцию
(285)
где - «подходящая»
функция; - предварительно найденная
первая собственная форма.
Коэффициент 
следует принять таким,
чтобы форма 
была ортогональна
первой собственной форме :
Подставляя сюда (285), получим
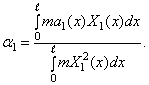
Далее от
нагрузки 
следует определить
прогибы 
. Если при помощи (285) первая форма исключена совершенно
точно, то функция будет ближе ко второй
форме, а последующие операции обеспечат сколь угодно близкое приближение к 
.
Однако первая
собственная форма может быть известна лишь приближенно, поэтому операция,
заключенная в (285), не гарантирует полного освобождения от первой формы 
. В связи с этим при продолжении процесса нужно снова
исправить функцию и принять
(286)
где коэффициент 
также определяется условием
ортогональности функций 
и :
которое
после подстановки (286) дает
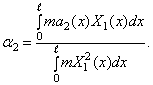
Затем следует
определить кривую 
от нагрузки 
, вновь исправить ее по формуле:
и т.д.
В таком процессе последовательных приближений ортогонализация сопровождает каждый шаг выкладок и, непрерывно вытесняя «примесь» первой формы, приведет ко второй собственной форме и второй частоте, которая, подобно (280), определится формулой
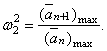
Таким же образом при помощи сопровождающей ортогонализации можно определить третью собственную форму и третью частоту и т.д.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Строительная механика Теория машин и механизмов
