Главная

Раздел 8. Вынужденные колебания систем с распределенными параметрами

Рассмотренные выше три способа решения задачи о вынужденных колебаниях систем с несколькими степенями свободы пригодны и для анализа колебаний систем с распределенной массой. Выбор способов обусловлен характером возмущающих сил: при гармоническом возмущении удобнее первый способ, а при произвольно заданном возмущении - третий.

8.1. Продольные колебания стержней

Рассмотрим случай, когда стержень испытывает действие одной сосредоточенной силы, изменяющейся по гармоническому закону:

(287)

Стационарные вынужденные колебания происходят с частотой возмущения и, значит, описываются законом:

(288)

где - подлежащая определению функция абсциссы (форма вынужденных колебаний). Для элемента стержня (см. рис.67,б) было получено уравнение:

(289)

где

(290)

Подставляя в (289) выражение (288), приходим к обыкновенному дифференциальному уравнению для функции

(291)

где определяется формулой (290).

Уравнение (291) отличается от (179) для формы свободных колебаний тем, что частота р заранее известна. Подобно выражению (181) решение уравнения (291) запишем в виде

(292)

Постоянные и определяются из граничных условий; рассмотрим некоторые из них.

Закрепленный конец стержня. В этом случае при любом , а это требует, чтобы в этом сечении .

К концу стержня приложена сила Она должна быть равна продольной силе в концевом сечении. Согласно (173),

(293)

Приравнивая (287) к (293), получим граничное условие в виде

(294)

Конец стержня свободен от нагрузки.

Согласно (294), здесь .

На конце стержня имеется сосредоточенная масса .

Развиваемая ею сила инерции

где - величины, относящиеся к точке расположения массы .

Эта сила инерции должна быть равна продольной силе

Следовательно, граничное условие имеет вид

Если стержень имеет переменное сечение, изменяющееся ступенчато, то решение (292) должно быть записано отдельно для каждого из участков:

. . . . . .

где - номер соответствующего участка.

Постоянные и определяются из двух условий на концах стержня и условий сопряжения, которые выражают равенство перемещений и продольных сил на границе двух участков:

Аналогично следует поступать и в тех случаях, когда возмущающая сила приложена в ряде промежуточных сечений.

Рассмотрим случай, когда внешняя нагрузка непрерывно распределена по длине стержня:

(295)

Используя рис.67,б, запишем уравнение движения с учетом элементарной внешней нагрузки ; тогда при помощи соотношения (288) при получим

Общее решение этого дифференциального уравнения зависит от вида правой части. Так, если

В общем случае решение имеет вид

(296)

Если сечение стержня меняется непрерывно, то исходное дифференциальное уравнение записывается так:

При этом предполагается отсутствие распределенной внешней нагрузки.

После подстановки выражения (288) уравнение принимает форму

(297)

Это уравнение имеет переменные коэффициенты и в общем случае не может быть решено в замкнутом виде, поэтому приходится использовать приближенные методы.

Теперь рассмотрим разложение решения в ряд по собственным функциям.

В общем случае внешняя нагрузка произвольным образом распределена по длине и является какой угодно функцией времени:

В частности, нагрузка может изменяться во времени по закону, общему для всех точек:

(298)

Согласно рис.67, учитывая элементарную внешнюю нагрузку , получим при

(299)

Далее нагрузка и перемещение представляются в виде рядов по собственным функциям соответствующей задачи о свободных колебаниях:

(300)

Для определения функций времени умножим обе части уравнения (299) на и проинтегрируем результат по всей длине стержня. При интегрировании в правой части исчезнут все слагаемые, кроме -го, вследствие ортогональности собственных функций, и для получится формула

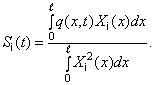(301)

Если нагрузка меняется по закону (298), то

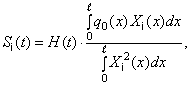(302)

т.е. функции для всех номеров отличаются только масштабом.

Если же нагружение осуществляется сосредоточенными силами в сечениях с абсциссами то (301) принимает вид

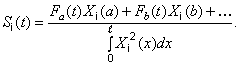(303)

Определение функций основано на том, что каждое слагаемое в правой части верхнего ряда (300) вызывает движение, определяемое соответствующим слагаемым нижнего ряда (300). Поэтому в (299) можно подставить

(304)

Тогда получим уравнение

или после деления на

Это равенство выполняется при условии, что обе его части равны одному и тому же числу, которое обозначим через .

Тогда

Решение этого уравнения имеет вид

Эта формула и позволяет решить задачу, так как дает возможность образовать вторую из сумм (300). Если нагрузка следует закону (298), то при учете выражения (302) можно записать

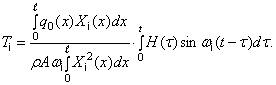
В случае произвольной периодической функции следует воспользоваться способами, изложенными выше. В простейших случаях [например, когда нагрузка определяется выражением (295)] удобнее искать решение в виде (288), определяя по (296).

8.2. Изгибные колебания балок

Рассмотрим случай, когда возмущающая нагрузка задана в виде сосредоточенной силы

(305)

или комбинации нескольких нагрузок того же вида с одинаковой частотой. Решение для прогибов будем искать в виде

(306)

сводя задачу к определению формы колебаний (кривой амплитуд прогибов) .

В случае , подставляя в (192) (306), получим

(307)

Решение дифференциального уравнения (307) имеет вид

(308)

где - функции Крылова (198), в которых вместо (196) нужно принять

Для определения постоянных , входящих в общее решение (308), необходимо использовать граничные условия. Рассмотрим два случая, которые не освещались при расчете на свободные колебания.

1.Возмущающая сила приложена на конце балки. Поперечная сила в сечении должна быть равна этой силе

и граничное условие принимает вид

где знак «+» соответствует силе, приложенной к правому концу, знак «-» - силе, приложенной к левому концу. Кроме того, .

2. Возмущающая сила приложена в промежуточном сечении балки.

В этом сечении должны выполняться четыре условия сопряжения:

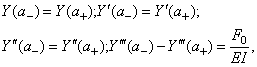
где а - абсцисса сечения, в котором приложена возмущающая сила; индексы «-» и «+» соответствуют сечениям, расположенным бесконечно близко слева и справа от сечения а.

Первые три условия обозначают непрерывность прогиба, угла поворота сечения и изгибающего момента в точке приложения возмущающей силы; четвертое условие выражает разрыв функции поперечной силы в указанном сечении на величину .

Приведенные выше рассуждения представляют собой непосредственное решение задачи. Теперь рассмотрим другой способ - разложение решения в ряд по собственным функциям.

В общем случае, когда возмущающая поперечная нагрузка задана произвольным законом

дифференциальное уравнение движения приобретает вид

(309)

т.е. отличается от аналогичного уравнения при свободных колебаниях наличием правой части.

Как и выше, представим в виде ряда

(310)

Также в виде ряда будем искать решение для прогиба

(311)

Для определения функций времени умножим обе части равенства (310) на и проинтегрируем результат по всей длине балки. Вследствие ортогональности собственных функций в правой части при этом остается только одно слагаемое, соответствующее номеру , так что

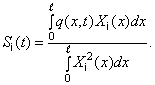(312)

Эта формула совпадает по записи с (301), выведенной выше для продольных колебаний, но в (312) представляет собой собственные формы задачи о свободных колебаниях балки («балочные функции»). Поэтому здесь также справедлива формула (303), относящаяся к случаю сосредоточенных возмущающих сил.