Главная
Раздел 9. Колебания пластин и оболочек
Задачи об определении частот и форм собственных колебаний пластин и оболочек приводят к необходимости интегрирования дифференциальных уравнений в частных производных. Наиболее хорошо изучены те случаи, когда оказывается возможным разделение переменных. К ним относятся, в частности, колебания прямоугольной пластины, шарнирно опертой по противолежащим сторонам, зонтичные и веерные колебания круглых осесимметричных пластин, колебания цилиндрических оболочек, замкнутых или шарнирно закрепленных вдоль образующих.
Если разделение переменных оказывается невозможным, то для расчета, в основном, используют приближенные и численные методы.
9.1.
Уравнение движения пластины постоянной толщины
Расположим
оси 
и 
в срединной плоскости
пластины, ось 
направим по нормали к
этой плоскости. Дифференциальное уравнение статического изгиба пластины
постоянной толщины 
при малых перемещениях
имеет вид
где 
- бигармонический
оператор;
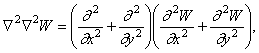
- прогиб;
- цилиндрическая
жесткость;
- интенсивность
нормальной нагрузки.
Добавляя к внешней нагрузке интенсивность сил инерции,
(313)
где 
- плотность материала,
получим уравнение движения
(314)
При свободных
колебаниях нагрузка 
, и решение уравнения (314) ищется в виде
(315)
Подставляя
(315) в однородное уравнение, соответствующее (314), получим для амплитудной
функции 
уравнение в частных
производных
(316)
где 
Уравнение
(316) может быть представлено так:
откуда следует, что решениями (316) являются, в частности, решения более простых уравнений:
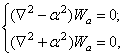(317)
или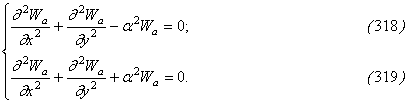 
Из бесчисленного множества решений уравнения (316) должны быть отобраны те, которые соответствуют условиям закрепления краев пластинки. Эти условия будут такими же, как и при статическом изгибе: на жестко защемленном краю
на
шарнирно опертом краю
на
свободном краю
где 
и 
- амплитудный
изгибающий момент и приведенная поперечная сила на контуре.
Если пластина
отнесена к декартовой системе координат 
то и определяются формулами
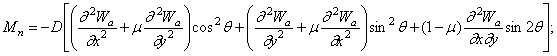
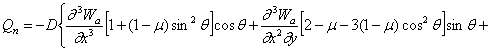
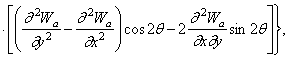
где 
- угол, образуемый
внешней нормалью к контуру с осью х; 
- радиус кривизны
контура.
9.2.
Прямоугольная пластина постоянной толщины
9.2.1.
Пластина, шарнирно опертая по противолежащим сторонам
Точное решение задачи об определении собственных частот и форм колебаний прямоугольной пластины может быть получено, если две противолежащие стороны пластины имеют шарнирное опирание. При этом закрепление двух других сторон может быть произвольным.
Пусть у
прямоугольной пластины размерами (
- размер вдоль оси ; 
- вдоль оси ) шарнирно оперты края 
и 
.
Тогда выражение для амплитудных прогибов, удовлетворяющее условиям шарнирного опирания на этих краях, можно представить в виде
Подставляя
это выражение в (318) и (319), устанавливаем, что функция 
должна удовлетворять
одному из двух уравнений:
где 
или
где 
Решениями
этих уравнений являются выражения 
Следовательно, общее
выражение для 
принимает вид
Это выражение
должно удовлетворять граничным условиям при 
Если эти края пластины
также шарнирно оперты, то должно быть
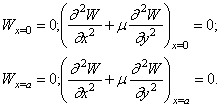
Из условий
при 
находим
Условия при 
приводят к уравнениям
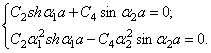
Приравнивая нулю определитель этой системы уравнений, получим частотное уравнение
которое
выполняется при 
Так как 
, то 
Тогда собственные частоты пластинки, шарнирно опертой по контуру, определяются формулой
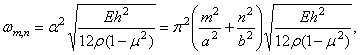(320)
где 
Низшая
частота 
соответствует 
т.е. колебаниям
пластинки без узловых линий:
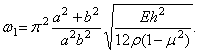
Форма колебаний определяется выражением
(321)
Аналогичным
образом проводится расчет и при других условиях закрепления границ
9.2.2.
Асимптотический метод расчета пластин
Для прямоугольной пластины с закреплением, отличным от шарнирного опирания по противолежащим сторонам, применяют различные приближенные методы. Рассмотрим асимптотический метод.
В пластинках так же как и в балках, имеет место динамический краевой эффект, который заключается в том, что закрепление влияет на форму колебания только вблизи границы, а вдали от нее форма колебания определяется произведением синусов типа уравнения (321). Благодаря этому колебания можно представить как сумму функции типа (321) и быстро затухающих с удалением от границ функций, которые позволяют выполнить граничные условия.
Рассмотрим
применение этого метода на примере заделанной по контуру прямоугольной пластины
размерами 
, у которой, как и ранее, размер а соответствует оси . Ограничимся расчетом симметричных относительно осей 
форм колебаний. В
средней части пластины (начало координат располагается в центре тяжести
пластины) принимаем
Вблизи границ
:
где - быстро изменяющаяся функция,
позволяющая удовлетворить условиям закрепления.
Аналогично
вблизи границ 
:
Таким
образом, общее выражение для имеет вид
(322)
В средней
части пластинки функции и 
пренебрежимо малы и
поэтому первый член выражения (322) должен удовлетворять уравнению (316).
Отсюда находим
Вблизи границ
существенными являются
первый и второй члены выражения (322). Учитывая, что первый член удовлетворяет
уравнению (316), потребуем, чтобы и второй удовлетворял ему:
Выполняя дифференцирование, приходим к уравнению:
которое
распадается на два уравнения:
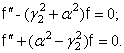
Так
как 
, то затухающие решения имеет только первое из этих
уравнений. Решение, затухающее с удалением от стороны 
, имеет вид
где
В
силу симметрии вблизи стороны 
:
Аналогично вблизи стороны 
:
где
и вблизи стороны 
:
Рассмотрим
граничные условия при :
При
вычислении и 
учтем, что практически
вдоль всей стороны , за исключением окрестностей угловых точек, функция равна нулю, поэтому определяется первыми
двумя слагаемыми выражения (322):
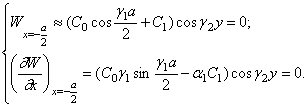
Для
одновременного выполнения этих уравнений необходимо, чтобы определитель,
составленный из коэффициентов при 
и 
, равнялся нулю, что приводит к уравнению:
(323)
Аналогично
условия при 
приводят к уравнению:
(324)
Так как 
связаны с 
, то трансцендентные уравнения (323) и (324) позволяют
определить значения 
и 
, а затем вычислить 
и частоты:
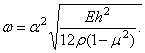
Рассмотрим,
например, колебания квадратной пластинки с одинаковым числом узловых линий в
направлениях . В этом случае 
и уравнения (323) и
(324) приводят к зависимости:
,
откуда
Частоты колебаний определяются формулой:
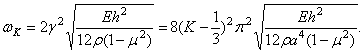
Достаточно хороший результат получается уже для низшей частоты:
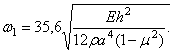
Точное значение:
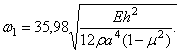
Как видно из вышеизложенного, при использовании асимптотического метода погрешность возникает вследствие приближенного выполнения граничных условий вблизи угловых точек.
9.3. Круглая
пластина постоянной толщины
9.3.1.
Определение форм и частот колебаний
Для круглой
пластины в уравнениях (317) для амплитудной функции 
следует перейти к
полярным координатам 
. В этих координатах оператор Лапласа имеет вид
Таким образом, уравнение (317) в полярных координатах принимает форму
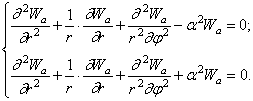(325)
Решения этих уравнений, соответствующие колебаниям пластины с n узловыми диаметрами, можно представить в виде
После подстановки этого выражения приходим к уравнениям:
(326)
(327)
Решениями
уравнения (326) являются бесселевы функции порядка 
первого 
и второго 
рода; решениями
уравнения (327) - модифицированные бесселевы функции 
, 
. Таким образом, общее выражение амплитудной функции с 
узловыми диаметрами
таково:
(328)
Для кольцевой
пластинки имеются четыре граничных условия (по два на каждом краю), которые образуют
однородную систему уравнений относительно констант 
Для сплошной пластинки
в выражении (328) равны нулю коэффициенты 
и 
при функциях,
стремящихся к бесконечности при 
Граничные условия на
внешнем контуре пластинки образуют в этом случае однородную систему уравнений
относительно и 
. Частотное уравнение получается путем приравнивания нулю
определителя системы.
В качестве примера рассмотрим колебания свободной сплошной круглой пластинки. В этом случае на контуре должны выполняться условия:
Изгибающий момент определяется формулой
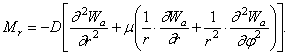
Поперечная сила:
Крутящий момент:
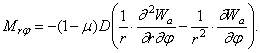
Таким образом, граничные условия имеют вид
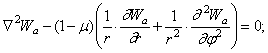
(329)
Учитывая, что
является решением
уравнения 
, а 
- уравнения 
, находим
При
подстановке в (329) вместо его выражения
учтем
правила дифференцирования функций Бесселя:
В результате приходим к уравнениям
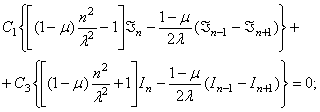
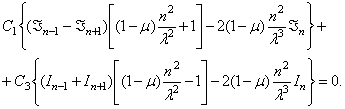
Здесь
аргументом всех бесселевых функций является величина 
, где 
- радиус пластинки.
Значения 
, обращающие в нуль определитель полученной системы, связаны
с собственными частотами равенством
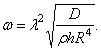
Если
ограничиться формами колебаний без узловых окружностей, то значениям 
и 
соответствуют смещения
пластинки как жесткой и нулевые частоты. При 
(два узловых диаметра)
частотное уравнение можно привести к виду
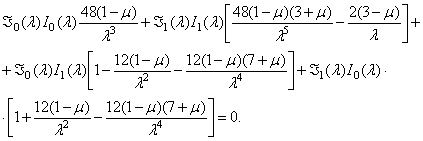
При 
наименьший корень этого уравнения 
и соответствующая частота собственных колебаний
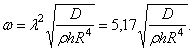
Для заделанной по контуру пластинки граничные условия
Частотное уравнение
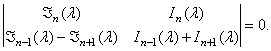
9.3.2.
Бегущие волны в круглых пластинках
Рассмотренные выше собственные колебания круглых пластинок описываются уравнением
(330)
Они соответствуют стоячим волнам на поверхности пластинки, при которых узловые диаметры неподвижны.
Наряду с (330) решением уравнения движения является также выражение
(331)
Но поскольку уравнение движения линейно, сумма и разность (330) и (331) также являются его решениями:
Эти выражения
представляют собой уравнения бегущих волн. Первое выражение соответствует
вращению всей картины деформаций вокруг оси симметрии пластинки в направлении
возрастания угла 
с угловой скоростью 
.
Второе выражение соответствует движению волны с той же скоростью в
противоположном направлении.
Если имеются
внешние нагрузки, вращающиеся по периферии пластинки со скоростью, близкой к
скорости распространения собственных колебаний, то такие
нагрузки вызовут большие резонансные колебания пластинки.
Практически движущаяся по круглой пластинке нагрузка осуществляется в дисках турбомашин благодаря вращению диска при неподвижной в пространстве нагрузке, обусловленной неравномерностью давления рабочего тела по окружности.
Критические
скорости вращения диска 
могут быть найдены, если известны частоты его
собственных колебаний 
,
по формуле
,
(332)
где - число узловых диаметров при свободных колебаниях
с частотой .
9.4.
Применение метода Рэлея-Ритца к определению частот собственных колебаний
пластинок
Метод Рэлея-Ритца позволяет расчетным путем приближенно определять частоты собственных колебаний пластинок переменной толщины и, в частности, дисков турбомашин. Преимуществом этого метода является также возможность легко учесть влияние на частоту различных побочных факторов, например начальных напряжений в срединной поверхности пластинки.
Потенциальная
энергия деформации пластинки при ее изгибе по форме, определяемой функцией , выражается двойным интегралом
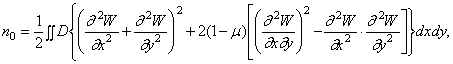(333)
где 
; интеграл берется по всей поверхности пластинки, причем для
пластинки постоянной толщины, заделанной по контуру, интеграл от второго
слагаемого выражения (333) обращается в нуль.
Обобщенная масса пластинки
(334)
В соответствии с методом Рэлея-Ритца форма колебаний задается в виде ряда
(335)
где каждая из
координатных функций 
удовлетворяет
геометрическим граничным условиям.
Равенство нулю определителя системы уравнений
(336)
позволяет
определить частоты собственных колебаний.
Если в (335) ограничиваются одним слагаемым, то частота определяется по формуле Рэлея
(337)
Можно задаваться
выражением для формы колебаний, в которое параметры 
входят нелинейно
В этом случае уравнения метода Рэлея-Ритца (336) оказываются нелинейными и проще исходить не из них, а из условий экстремума выражения (337), причем значения параметров, при которых достигается этот экстремум, находятся численными методами.
Рассмотрим в качестве примера заделанную по контуру прямоугольную пластинку постоянной толщины. Ограничиваясь одним слагаемым выражения (335), принимаем
.
Проводя вычисления по (333) и (334), находим
Для частоты колебаний получаем
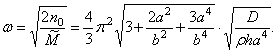
При 
:
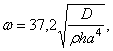
что
на 3,3 % выше точного значения.
При расчете
колебаний круглых пластин целесообразно использовать выражения энергии
деформации и обобщенной массы в полярных координатах
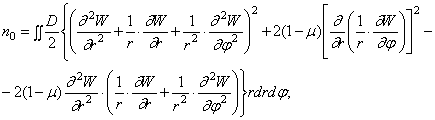
где
интегрирование выполняется по всей срединной поверхности пластинки.
При изучении колебаний осесимметричных пластин полагают
В этом случае
интегрирование по можно выполнить в
общем виде и выражения для 
и 
представляются в форме
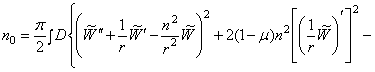
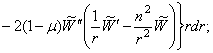(338)
(339)
Для сплошной
свободной пластинки вычисления упрощаются, если принять функцию 
в виде
где 
- параметр,
определяемый из условия минимума формулы Рэлея (337).
Тогда и определяются формулами
Чтобы оценить погрешность метода, применим его для расчета частоты колебаний диска постоянной толщины при двух узловых диаметрах. В этом случае
;
Отсюда находим
Минимальное
значение частоты при 
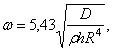
что
дает ошибку порядка 5 %.
9.5.
Колебания оболочек
Изгибные колебания пластинок можно рассматривать независимо от их колебаний в своей плоскости. В отличие от этого при колебаниях оболочек изгиб стенки связан, как правило, с растяжением срединной поверхности. Потенциальная энергия деформации оболочки выражается формулой
где
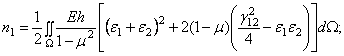(340)
(341)
Величина 
представляет собой
энергию растяжения оболочки, 
- энергию ее изгиба; 
- компоненты
деформации срединной поверхности; 
- параметры изменения
ее кривизны. Интегрирование в (340) и (341) выполняется по всей срединной
поверхности 
оболочки. Величины , по известным формулам
выражаются через компоненты амплитудного перемещения 
точек оболочки.
Амплитудное
значение кинетической энергии движения оболочки, совершающей гармонические
колебания с частотой 
,
Частота колебаний определяется формулой Рэлея
(342)
Числитель и
знаменатель дроби (342) зависят от выбора функции перемещений . При этом истинные формы собственных колебаний сообщают
выражению (342) стационарные значения, а первая собственная форма - минимум.
Обозначим характерный размер оболочки и характерную толщину через и 
соответственно.
Тогда (342) можно записать так:
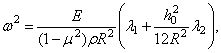(343)
где
Величины 
и 
являются безразмерными
и зависят от вида амплитудных функций . Второе слагаемое в (343), соответствующее энергии изгиба
оболочки, имеет малый множитель 
, поэтому при минимизации 
наиболее существенно
уменьшение 
, т.е. слагаемого, соответствующего энергии растяжения
срединной поверхности.
Если
геометрия оболочки и условия ее закрепления это допускают, то наименьшие
значения частот отвечают такому выбору функций , при котором 
Но требование
может быть выполнено
только при 
, т.е. при отсутствии растяжения срединной поверхности. Такой
вид деформации оболочек называется чистым
изгибанием.
9.5.1.
Теория колебаний оболочек без растяжения срединной поверхности
На основе
описанной выше теории рассмотрим колебания цилиндрической оболочки (рис.75).
Определим положение произвольной точки 
на срединной
поверхности оболочки координатами 
и 
.
Рис.75
Компоненты
перемещения точки в продольном, окружном и нормальном к поверхности
направлениях обозначим соответственно . Компоненты деформации срединной поверхности определяются
формулами
(344)
Приравняв 
и 
нулю и проинтегрировав
полученные уравнения, выразим через две произвольные
функции угловой координаты
(345)
Из полученных формул видно, что при деформации цилиндрической оболочки без растяжения срединной поверхности образующие остаются прямыми, а осевые перемещения не зависят от продольной координаты.
Формулы
показывают, что чистые изгибания замкнутой цилиндрической оболочки возможны в
следующих случаях: а) если ее торцы свободны; в этом случае отличны от нуля 
и 
; б) если на одном из торцов запрещены перемещения 
, но разрешено перемещение 
; в) если на одном из торцов запрещено перемещение . Если же оболочка оперта на обоих торцах, чистое изгибание
ее невозможно.
Составим
выражения потенциальной и кинетической энергии оболочки, совершающей
гармонические колебания с частотой . В общем выражении потенциальной энергии деформации
сохраняется только слагаемое . Входящие в него параметры изменения кривизны определяются
формулами
После
подстановки этих значений в выражение (341) и интегрирования
по 
с учетом того, что 
, находим
(346)
где
Интегралы в
выражениях 
вычисляются по всей
длине оболочки.
Из основного
уравнения метода Рэлея-Ритца следует, что выражение 
(где - частота собственных
колебаний) должно иметь стационарное значение:
Отсюда
следует система обыкновенных дифференциальных уравнений для функции 
,
. В этом случае, если форма всех меридиональных сечений
одинакова (толщина оболочки не зависит от ), коэффициенты постоянны и уравнения
получают такой вид:
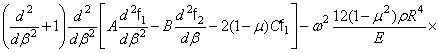
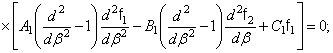(347)
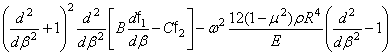
. (348)
Решение этих
дифференциальных уравнений для открытых оболочек должно быть подчинено
граничным условиям на продольных кромках. На этих кромках могут быть заданы
перемещения (постоянные вдоль
каждой кромки), а также перемещения и угол поворота
в
двух различных сечениях по длине оболочки. Всего имеется семь кинематических
граничных условий на каждой продольной кромке, что соответствует четырнадцатому
порядку уравнений (347)-(348). Если закрепления отсутствуют, то кинематические
граничные условия заменяются естественными граничными условиями.
Если оболочка
симметрична относительно поперечного сечения 
(рис.76,а), то 
и функции , определяются
независимыми дифференциальными уравнениями
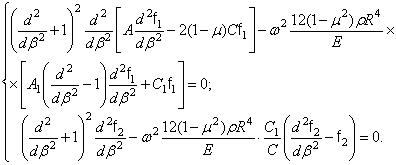(349)
Функция описывает в этом
случае кососимметричные относительно сечения формы колебаний, а
функция - симметричные.
Уравнение, определяющее функцию 
, совпадает с уравнением колебаний кольца в своей плоскости.
Рис.76
Для замкнутой
оболочки граничные условия заменяются условиями периодичности, которым
удовлетворяют функции 
, 
. В случае симметричной оболочки подстановка этих выражений в
уравнения (349) приводит к следующим значениям частот для кососимметричных
колебаний:
и для симметричных колебаний:
.
Для оболочки
постоянной толщины и длины 
(рис.76,б):
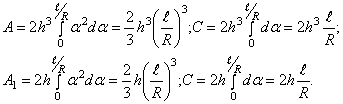
В этом случае
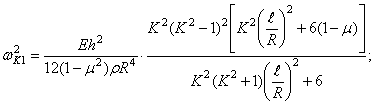
Как видно из полученных формул, при колебаниях оболочек без растяжения срединной поверхности частоты определяются зависимостями такого же типа, как и для пластинок
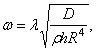
где 
- цилиндрическая
жесткость; - числовой
коэффициент. При стремлении толщины оболочки к нулю частота ее колебаний без
растяжения срединной поверхности также стремится к нулю.
9.5.2.
Уравнения движения оболочек
Если отнести
оболочку к системе гауссовых координат 
, совпадающих с линиями кривизны срединной поверхности, то
уравнения движения могут быть записаны в таком виде:
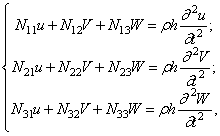(350)
где - компоненты
перемещения точки срединной поверхности в направлениях - и -линий и по нормали; 
- масса оболочки на
единицу срединной поверхности; 
- дифференциальные
операторы. Структура операторов для оболочек
произвольной формы весьма сложна. Поэтому уравнения движения в виде (350), т.е.
в перемещениях, имеет смысл записывать только для простейшего случая
цилиндрической оболочки постоянной толщины, для которой коэффициенты уравнений
постоянны. В этом случае
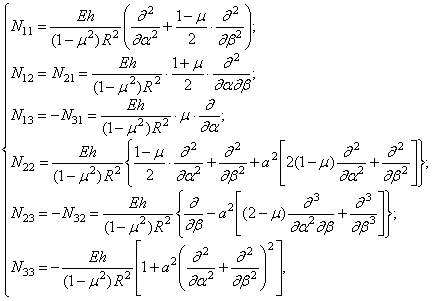(351)
где ; 
- безразмерные
координаты точки на срединной поверхности; 
.
Система
уравнений (350) имеет восьмой порядок по координатам и второй - по времени 
. Даже тогда, когда эти уравнения имеют постоянные
коэффициенты (т.е. для цилиндрической оболочки) и при рассмотрении
гармонических колебаний с частотой , т.е. при
аналитическое
решение этих уравнений может быть получено лишь при некоторых специально
подобранных граничных условиях. В остальных случаях для расчета используют
приближенные или численные методы.
Особенностью
уравнений движения оболочек является то, что, как это видно из формул (351), в
эти уравнения входит малый, пропорциональный квадрату толщины оболочки,
параметр 
, на который умножаются старшие производные перемещений по
координатам. Поэтому, если рассматриваются такие формы колебаний, при которых
перемещения медленно меняются по координатам и , соответствующими моментными членами в уравнениях (350)
можно пренебречь. На основе безмоментной теории рассматривают низшие формы
колебаний оболочек, закрепленных так, что обеспечивается возможность безмоментного
состояния.
При высших
формах собственных колебаний оболочка разбивается узловыми линиями на ряд
достаточно пологих сегментов, на каждом из которых напряженное состояние быстро
изменяется по координатам. В этом случае для расчета может быть использована
так называемая теория пологих оболочек. Применительно к цилиндрической оболочке
уравнения теории пологих оболочек получаются из уравнений (350), если в
операторах 
(351) опустить
слагаемые с множителем .
Аналитическое
решение задачи о собственных колебаниях для замкнутой цилиндрической оболочки
может быть получено при так называемых граничных условиях Навье. Согласно этим
условиям, на торцах оболочки отсутствуют нормальные 
и окружные 
перемещения, а также
продольная сила 
в срединной
поверхности и изгибающий момент 
. Условиям Навье удовлетворяют следующие выражения
компонентов перемещения:
Подставив эти
выражения в уравнения движения (350) и учитывая (351), придем к системе трех
линейных алгебраических уравнений относительно 
.
Равенство
нулю определителя этой системы приводит к кубическому уравнению относительно . Три корня этого уравнения соответствуют трем различным
формам колебаний с одинаковыми числами узловых окружностей и образующих, но с
различными соотношениями между .
В отличие от пластинок, где наименьшие собственные частоты соответствуют формам колебаний без узловых линий, в оболочках, закрепленных так, что деформация их без растяжения срединной поверхности невозможна, наименьшие частоты имеют колебания с узловыми линиями. Это объясняется тем, что формы колебаний без узловых линий связаны со значительными деформациями в срединной поверхности оболочки.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Строительная механика Теория машин и механизмов
