Главная

Расчет зубчатых передач и валов

Задача 1.

1. Рассчитать закрытую цилиндрическую прямозубую передачу.

2. Рассчитать и сконструировать ведомый вал передачи.

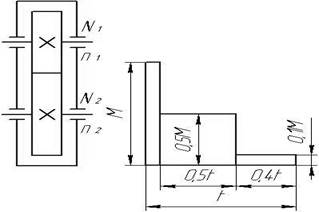
Рис. 1. Схема редуктора Рис. 2. График нагрузки

Таблица 1. Исходные данные задачи № 1

Номер варианта	N2	n1	n2	L	n, сут	К, год
1	10	750	125	7	0,3	0,7
2	11	750	150	6	0,4	0,6
3	12	750	175	5	0,5	0,5
4	13	750	200	4	0,6	0,4
5	14	750	225	5	0,7	0,3
6	15	750	250	6	0,8	0,4
7	16	750	275	7	0,	0,5
8	17	1000	175	3	70,6	0,8
9	18	1000	200	4	0,5	0,6
10	19	1000	225	5	0,4	0,7
11	20	1000	250	6	0,5	0,8
12	21	1000	275	7	0,6	0,7
13	22	1000	300	8	0,7	0,6
14	23	1000	325	7	0,8	0,5
15	24	1000	350	6	0,9	0,4
16	25	1500	300	5	0,8	0,3
17	24	1500	325	4	0,7	0,4
18	23	1500	350	3	0,6	0,5
19	22	1500	375	4	0,5	0,6
20	21	1500	400	5	0,4	0,7
21	20	1500	425	6	0,3	0,8
22	19	1500	450	7	0,4	0,7
23	18	3000	500	8	0,5	0,6
24	17	3000	525	7	0,6	0,5
25	16	3000	550	6	0,7	0,4
26	15	3000	575	5	0,8	0,3
27	14	3000	600	4	0,9	0,4
28	13	3000	625	8	0,8	0,5
29	12	3000	650	7	0,7	0,6
30	11	3000	675	6	0,6	0,3

Задача 2.

1. Рассчитать закрытую коническую косозубую передачу.

2. Рассчитать и сконструировать ведомый вал передачи.

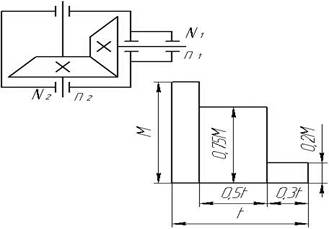
Рис. 3. Схема редуктора Рис. 4. График нагрузки

Таблица 2. Исходные данные задачи № 2

Номер варианта	N2	n1	n2	L	n, сут	К, год
1	50	1500	450	5	0,5	0,8
2	70	1500	400	6	0,6	0,7
3	65	1500	250	7	0,7	0,6
4	60	1500	350	8	0,8	0,5
5	55	1500	700	9	0,5	0,4
6	50	3000	1500	10	0,6	0,3
7	45	3000	750	9	0,7	0,4
8	40	3000	375	8	0,8	0,5
9	35	3000	500	7	0,9	0,6
10	30	3000	1000	6	0,8	0,7
11	28	3000	600	5	0,6	0,8
12	26	3000	700	4	0,5	0,9
13	24	1500	400	4	0,4	0,8
14	22	1500	375	5	0,3	0,7
15	20	1500	325	6	0,9	0,6
16	18	1500	300	7	0,8	0,5
17	16	1500	425	8	0,7	0,4
18	14	1500	475	9	0,6	0,3
19	12	1500	525	10	0,5	0,6
20	11	1000	200	9	0,4	0,7
21	10	1000	225	8	0,3	0,8
22	9	1000	250	7	0,4	0,8
23	8	1000	275	6	0,5	0,7
24	7	1000	300	5	0,6	0,7
25	6	1000	325	6	0,7	0,8
26	5	750	150	7	0,8	0,6
27	4	750	175	8	0,9	0,5
28	3	750	190	9	0,7	0,4
29	2	750	210	7	0,6	0,8
30	1	750	240	4	0,5	0,7

Задача 3.

1. Рассчитать закрытую цилиндрическую косозубую передачу.

2. Рассчитать и сконструировать ведомый вал передачи.

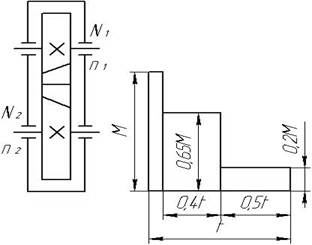
Рис. 5. Схема редуктора Рис. 6. График нагрузки

Таблица 3. Исходные данные задачи № 3

Номер варианта	N2	n1	n2	L	n, сут	К, год
1	20	3000	1115	4	0,7	0,6
2	22	3000	925	5	0,8	0,7
3	24	3000	810	6	0,6	0,5
4	26	3000	725	7	0,5	0,6
5	28	3000	600	8	0,4	0,3
6	30	1500	550	9	0,3	0,4
7	32	1500	520	10	0,2	0,8
8	34	1500	425	4	0,4	0,6
9	36	1500	525	5	0,6	0,3
10	38	1500	410	6	0,5	0,8
11	40	1250	350	7	0,6	0,7
12	42	1250	295	8	0,7	0,5
13	44	1250	245	9	0,8	0,4
14	46	1250	210	10	0,7	0,5
15	48	1250	290	8	0,6	0,8
16	50	1000	295	9	0,5	0,9
17	52	1000	240	7	0,4	0,7
18	54	1000	195	6	0,3	0,6
19	56	1000	160	5	0,2	0,9
20	58	1000	405	4	0,3	0,8
21	60	1000	315	5	0,4	0,6
22	62	850	245	6	0,5	0,7
23	64	850	210	7	0,6	0,5
24	66	850	165	8	0,7	0,5
25	68	850	150	9	0,8	0,4
26	56	700	240	8	0,7	0,3
27	58	700	215	7	0,6	0,5
28	50	700	165	6	0,5	0,7
29	54	700	130	5	0,4	0,8
30	52	700	115	4	0,3	0,9

Задача 4.

1. Рассчитать закрытую коническую прямозубую передачу.

2. Рассчитать и сконструировать ведомый вал передачи

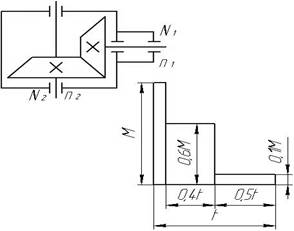
Рис. 7. Схема редуктора Рис. 8 График нагрузки

Таблица 4. Исходные данные для задачи № 4

Номер варианта	N2	n1	n2	L	n, сут	К, год
1	1,2	650	105	9	0,3	0,5
2	1,4	650	130	8	0,4	0,6
3	1,6	650	165	7	0,5	0,7
4	1,8	650	210	5	0,6	0,3
5	2,0	750	200	3	0,7	0,4
6	2,2	750	230	4	0,8	0,5
7	2,4	750	275	6	0,7	0,3
8	2,8	750	310	8	0,6	0,4
9	3,0	750	380	9	0,5	0,7
10	3,2	900	150	7	0,4	0,8
11	3,4	900	175	5	0,3	0,9
12	3,6	900	210	3	0,2	0,7
13	3,8	900	265	4	0,3	0,6
14	4,0	900	320	6	0,4	0,5
15	4,2	1100	200	8	0,5	0,4
16	4,4	1100	245	9	0,6	0,3
17	4,6	1100	290	7	0,7	0,5
18	4,8	1100	315	5	0,8	0,4
19	5,0	1100	480	3	0,7	0,3
20	6,2	1250	260	4	0,6	0,3
21	7,2	1250	285	6	0,5	0,4
22	8,2	1250	315	8	0,4	0,6
23	9,2	1250	410	7	0,3	0,7
24	10,2	1250	440	5	0,2	0,8
25	11,2	1500	310	4	0,4	0,9
26	13	1500	340	6	0,3	0,8
27	15	1500	365	7	0,5	0,6
28	17	1500	515	8	0,7	0,4
29	19	1500	620	4	0,4	0,7
30	21	3000	600	5	0,5	0,6

Задача 5.

1. Рассчитать закрытую червячную передачу.

2. Рассчитать и сконструировать ведомый вал передачи

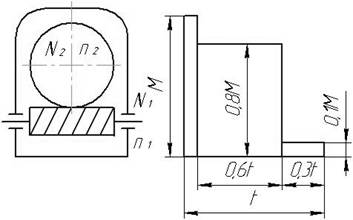
Рис. 9. Схема редуктора Рис. 10. График нагрузки

Таблица 5. Исходные данные для задачи № 5

Номер варианта	N2	n1	n2	L	n, сут	К, год
1	0,5	1200	220	7	0,4	0,8
2	0,7	200	260	6	0,5	0,7
3	0,9	1200	295	5	0,6	0,5
4	1,1	1200	315	4	0,7	0,4
5	1,3	1200	430	6	0,8	0,7
6	1,5	1500	260	8	0,7	0,4
7	1,7	1500	290	10	0,6	0,5
8	1,9	1500	340	9	0,5	0,7
9	2,0	1500	395	7	0,4	0,8
10	2,5	1500	480	5	0,3	0,9
11	3,5	750	125	6	0,2	0,7
12	4,5	750	250	8	0,8	0,3
13	5,5	750	310	5	0,6	0,4
14	9	750	260	6	0,4	0,6
15	13	750	340	7	0,2	0,9
16	17	3000	510	10	0,3	0,8
17	21	3000	485	11	0,5	0,4
18	25	3000	450	9	0,7	0,5
19	29	3000	675	8	0,8	0,6
20	35	3000	870	7	0,7	0,6
21	40	1000	190	4	0,6	0,8
22	45	1000	215	5	0,5	0,3
23	50	1000	285	6	0,4	0,7
24	55	1000	360	7	0,3	0,8
25	60	1000	425	8	0,2	0,9
26	55	600	105	9	0,3	0,7
27	50	600	130	10	0,4	0,5
28	45	600	170	4	0,5	0,6
29	40	600	190	6	0,6	0,7
30	35	600	285	7	0,7	0,8

Задача 6.

1. Рассчитать закрытую цилиндрическую шевронную передачу.

2. Рассчитать и сконструировать ведомый вал передачи

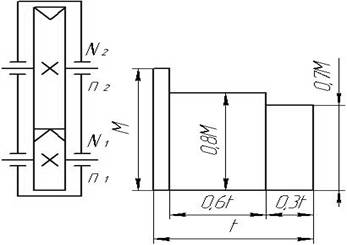
Рис. 11. Схема редуктора Рис. 12. График нагрузки

Таблица 6. Исходные данные для задачи № 6

Номер варианта	N2	n1	n2	L	n, сут	К, год
1	70	600	105	5	0,5	0,8
2	65	600	135	6	0,6	0,7
3	60	600	165	7	0,7	0,6
4	55	600	210	8	0,8	0,5
5	50	600	255	9	0,7	0,4
6	45	950	290	10	0,6	0,5
7	40	950	160	11	0,5	0,7
8	37	950	210	6	0,4	0,8
9	34	950	260	8	03,	0,9
10	31	950	310	10	0,2	0,7
11	28	1100	330	5	0,3	0,8
12	25	1100	345	7	0,4	0,7
13	22	1100	385	9	0,5	0,6
14	20	1100	180	11	0,6	0,4
15	18	1100	230	10	0,7	0,5
16	16	1100	250	8	0,8	0,4
17	14	1400	225	6	0,7	0,3
18	12	1400	255	4	0,6	0,5
19	10	1400	280	5	0,5	0,7
20	9	1400	340	7	0,4	0,3
21	8	1400	370	9	0,3	0,6
22	7,5	2000	325	11	0,2	0,8
23	6,5	2000	350	10	0,3	0,7
24	6	2000	400	9	0,4	0,5
25	5,5	2000	420	8	0,5	0,6
26	5	3000	520	7	0,6	0,5
27	4,5	3000	550	6	0,7	0,4
28	4	3000	600	7	0,8	0,5
29	3,5	3000	720	8	0,7	0,6
30	3	3000	850	9	0,6	0,7

Задача 7.

1. Рассчитать планетарную передачу. Нагрузка постоянная. Срок службы длительный.

2. Рассчитать и сконструировать ведомый вал передачи.

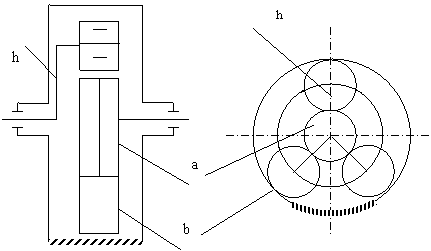
Рис. 13. Схема редуктора

Таблица 7. Исходные данные для задачи 7

Величина	Вариант
	1	2	3	4	5	6	7
Nа, кВт	6	8	10	12	14	16	18
nh, об/мин	1600	1500	1400	1300	1200	1100	1000
nа, об/мин	500	450	400	300	200	250	150
Величина	Вариант
	8	9	10	11	12	13	14
Nа, кВт	20	22	24	26	3	5	7
nh, об/мин	900	800	700	600	2000	1900	1800
nа, об/мин	180	100	90	80	400	350	300

Методические указания по выполнению расчетно-графических и контрольных работ

1. Последовательность расчета цилиндрических зубчатых передач

Исходные данные

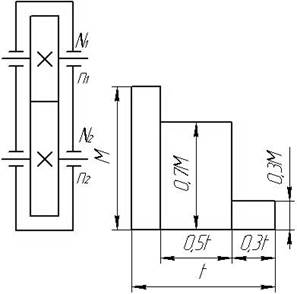
Рис.14 Схема передач Рис.15 График нагрузки

1.1. Определение коэффициента режима работы

1.1.1. Ресурс передачи

Ресурс передачи определяется по зависимости

1.1.2. Эквивалентное число циклов нагружения зубьев при расчете на контактную прочность

При n₁=n=const, M_max=M_н, для нашего случая эквивалентное число циклов нагружения зубьев шестерни

Эквивалентное число циклов нагружения для зубьев колеса

1.1.3. Эквивалентное число циклов нагружения зубьев при расчете на изгибную прочность

При n₁=n=const, M_max=M_н, для нашего случая

Эквивалентное число циклов нагружения для зубьев колеса

1.1.4. Расчет коэффициента долговечности для контактной прочности

Для нормализуемой и улучшенной сталей (HB≤350)

Если N_ц.экв≥10⁷ , то принять K_HL=1,0.

Для закаленных сталей и чугуна базовое число циклов принимают N_Б=25∙10⁷, а минимальное значение K_HL=0,585. Если N_ц.экв≥25∙10⁷ , то принять K_HL=0,585.

1.1.5. Определение коэффициента долговечности при расчете на изгиб

Если N_ц.экв≥5∙10⁶, то принять K_FL=1,0.

1.2. Определение допускаемых напряжений

1.2.1. Допускаемые контактные напряжения

Допускаемые контактные напряжения назначают в зависимости от принятого материала (табл. 8) и его термической обработки (табл. 9).

Для углеродистых и легированных сталей любых марок при HB≤350 (нормализация и улучшение) допускаемые контактные напряжения определяют по зависимости

где σ_Hlim – предел контактной выносливости при базовом числе циклов нагружения;

K_HL – коэффициент долговечности;

Z_R – коэффициент, учитывающий шероховатость поверхности зубьев;

Z_V – коэффициент, учитывающий окружную скорость (для приближенных расчетов можно принимать Z_RZ_V = 1,0);

S_H – коэффициент запаса (при нормализации и объемной закалке S_H =1,1…1,2; при поверхностном упрочнении S_H = 1,2…1,3).

Таблица 8. Допускаемые контактные и изгибные напряжения для зубчатых колес

Группа сталей	контактное σHlim, Мпа	SHmin	изгибное σHlim, Мпа	SF	[σH]max, МПа	[σF]max, МПа
40, 45, 40Х, 40ХН, 45ХЦ, 35ХМ	2HB + 70	1,1	1,8 HB	1,75	2,8σT	2,74 HB
40Х, 40ХН, 45ХЦ, 36ХМ	18HRC + 150		550		2,8σT	1400
55ПП, У6, 35ХМ	17НRCпов+	1,2	900		40HRCпов	1260
40Х, 40ХН 35ХМ, 40Х, 40ХН	+ 200 17НRCпов+ + 200		650 550		40HRCпов	>> 1430
35ХЮА, 38ХМЮА, 40Х 40ХФА, 40ХНМА	1050 >>		12HRCсердц+300 1,75		40HRCпов 30HRCпов	1000 >>
Цементируемые стали всех марок	23HRCпов		750	1,5	40HRCпов	1200
Молибденовые стали 25ХГМ, 25ХГНМ	23HRCпов		1000		40HRCпов	1520
Безмолибденовые стали 25ХГТ, 30ХГТ, 35Х	23HRCпов		750		40HRCпов	1520

Таблица 9. Термическая обработка сталей для зубчатых колес

Марка стали	σв, МПа	σТ, МПа	Термическая обработка
35	550	270	Нормализация
45	600	320	>>
45	780	540	Улучшение
45	890	650	>>
40Х	790	640	>>
40Х	900	750	>>
40Х	900	750	Улучшение + закалка ТВЧ
35ХМ	800	670	Улучшение
35ХМ	920	790	>>
35ХМ	920	790	Улучшение + закалка ТВЧ
40ХН	800	630	Улучшение
40ХН	920	750	>>
40ХН	920	750	Улучшение + закалка ТВЧ
20ХНМ	1000	800	Улучшение + цементация + закалка
18ХГТ	1000	800	>>
12ХНЗА	1000	800	>>
25ХГМ	1000	800	>>
40ХНМА	980	780	Улучшение + азотирование
35Л	550	270	Нормализация
45Л	680	440	Улучшение

Для прямозубых колес в качестве расчетного принимают допускаемое контактное напряжение для колеса, поскольку оно меньше, чем у шестерни.

Для косозубых и шевронных колес в качестве расчетного принимают среднее арифметическое значение

1.2.2. Допускаемые изгибные напряжения

Допускаемые изгибные напряжения выбирают для двух случаев нагружения.

1.2.2.1. Одностороннее действие нагрузки (отнулевой цикл)

где [n] – требуемый коэффициент запаса прочности, [n]=1,4…2,2;

K_FL – коэффициент долговечности при изгибе;

K_σ – эффективный коэффициент концентрации напряжений у ножки зуба, K_σ = 1,4…1,6;

σ_-1 – предел выносливости сталей:

для углеродистых сталей σ_-1≈0,43σ_В МПа;

для легированных сталей σ_-1≈0,35σ_В+(70…120) МПа.

1.2.2.2. Переменное направление нагрузки (симметричный знакопеременный цикл)

1.3. Определение коэффициента нагрузки и степени точности передачи

Во все зависимости для определения основных параметров зацепления и напряжений, возникающих при работе передачи, входит не номинальная, а расчетная нагрузка.

M_расч=M_uK=M_uK_динK_кц, (14)

где K – коэффициент нагрузки;

K_дин – коэффициент динамичности, зависит от величины окружной скорости и точности изготовления;

K_кц – коэффициент концентрации нагрузки, учитывает неравномерность распределения нагрузки по длине зуба за счет деформации валов и колес.

При выполнении проектного расчета, когда параметры передачи и окружная скорость еще неизвестны, принимают: при симметричном расположении колес относительно опор K=K_динK_кц=1,3; при несимметричном или консольном расположении K=K_динK_кц=1,5.

После определения размеров передачи значение коэффициента нагрузки уточняют по фактическим данным.

1.4. Назначение коэффициента ширины зуба 𝛙_a

Стандарт (ГОСТ 2185-88) устанавливает следующие значения ширины зуба (ψ_a=b/a_w):

Таблица 10. Значения ширины зуба

Прямозубые	косозубые	шевронные
0,16; 0,2; 0,25; 0,315; 0,4	0,315; 0,4; 0,5; 0,63	0,5; 0,63; 0,8; 1,0; 1,25

Рекомендации:

1. Меньшие значения каждого диапазона рекомендуется применять для коробок передач, а большие – для редукторов;

2. При консольном расположении колес значение ψ_a следует принимать меньше;

3. Для тихоходной ступени значение ψ_a следует принимать большим, чем для быстроходной;

4. Увеличение точности изготовления и монтажа позволяет увеличить значение ψ_a.

Ширина колеса (венец) b₂=a_wψ_a; ширина шестерни назначается больше – b₂=a_wψ_a+(4…5) мм.

1.5. Определение межосевого расстояния зубчатой передачи и модуля зацепления

Межосевое расстояние цилиндрической зубчатой передачи определяют по зависимости:

где [σ]_H – допускаемое контактное напряжение в МПа;

M₁ – номинальный крутящий момент на шестерне в Нмм;

U - передаточное число;

K_П – коэффициент, учитывающий влияние суммарной длины контактных линий на повышение нагрузочной способности передачи, для пряпозубых колес K_П=1,0; для косозубых колес: при твердости HB≤350 и β<25° K_П = 1,35…1,5 (меньшие значения при Z≤20, а большие – при Z₁>40); при твердости HB>350, а также при β>25° независимо от твердости К_П = 1,15.

Полученное значение a_w округляют до ближайшего стандартного значения по ГОСТ 2185-88 (табл.11).

Таблица 11. Стандартные значения межосевого расстояния, мм

1 ряд	40; 50; 63; 80; 100; 125; 160; 200; 250; 315; 400; 580
2 ряд	71; 90; 112; 140; 180; 224; 280; 355; 450; 560; 710

Модуль зацепления ориентировочно принимают по зависимости:

m=(0,01…0,02)a_w, мм. (16)

Полученное значение модуля округляем до ближайшего стандартного значения по ГОСТ 9563 – 88 (табл. 12).

Таблица 12. Стандартные значения модуля, мм

1 ряд	1,0; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10
2 ряд	1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11

1.6. Расчет чисел зубьев, фактического передаточного числа и угла наклона зуба

1.6.1. Определение числа зубьев

Суммарное число зубьев Z_c для прямозубых колес:

для косозубых и шевронных колес:

Угол наклона зуба β принимают:

Для косозубых колес β= 8⁰…15⁰; для шевронных колес β= 25⁰…40⁰.

Числа зубьев шестерни и колеса:

Полученные значения чисел зубьев округляют до целых чисел. Рекомендуется для шестерен быстроходных ступеней принимать Z₁ = 20…30, а для последующих ступеней Z₁ = 17…24.

Уточнение фактического передаточного числа.

Отклонение фактического передаточного числа от проектного (заданного) не должно превышать 3,5%.

Проверка условия сборки

Для прямозубых колес:

Если для прямозубых колес не удовлетворяется условие сборки, то передачу необходимо вписать в стандартное межосевое расстояние за счет корригирования.

Для косозубых колес уточняют фактический угол наклона зуба:

При этом угол наклона зуба не подлежит изменению и стандартизации, например β = 13⁰15^’

Затем назначают степень точности передачи (табл. 13), ориентируясь на окружную скорость:

Таблица 13. Рекомендуемая степень точности изготовления зубчатых передач

Степень точности	Окружная скорость, м/с
	прямозубые	непрямозубые
8 (пониженная)	до 8	до 12
7 (нормальная)	до 12	до 20
6 (повышенная)	до 20	до 31,5

1.7. Проверка действительных контактных напряжений

Проверка действительных контактных напряжений выполняется после уточнения величины коэффициента нагрузки и определения геометрических размеров зубчатых колес по зависимости:

где K – уточненное значение коэффициента нагрузки;

U – фактическое передаточное число.

Затем необходимо рассчитать отклонение действительного контактного напряжения σ_H и [σ]_H, отклонение не должно превышать +5…- 20%. При перегрузке необходимо увеличить межосевое расстояние до ближайшего большего из стандартного ряда.

1.8. Проверка прочности зубьев шестерни и колеса на изгиб

Проверка изгибных напряжений производится по формуле:

где P – окружное усилие, Н;

Y – коэффициент формы зуба, определяется в зависимости от числа зубьев: действительного для прямозубых колес и эквивалентного (Z_v) для косозубых и шевронных колес (Z_v=Z/cos³β), см табл. 14;

K_П – коэффициент повышения нагрузочной способности на изгиб косозубых и шевронных колес (его значения такие же, как и для расчета на контактную прочность):

m_n - нормальный модуль (стандартный модуль), мм.

Таблица 14. Коэффициент формы зуба Y

Число зубьев Zv	Зубчатые колеса внешнего зацепления при коэффициенте смещения исходного контура			Зубчатые колеса с внутренними зубьями
	-0,2	0	+0,2
12	0,239	0,308	0,378	-
14	0,266	0,330	0,392	-
16	0,302	0,355	0,408	-
18	0,330	0,377	0,424	-
20	0,348	0,389	0,431	-
22	0,367	0,402	0,437	-
24	0,384	0,414	0,445	-
26	0,400	0,426	0,455	-
28	0,408	0,434	0,458	0,942
30	0,416	0,440	0,464	0,916
35	0,431	0,452	0,473	0,863
40	0,445	0,465	0,485	0,825
45	0,452	0,471	0,490	0,795
50	0,459	0,477	0,495	0,769
60	0,474	0,490	0,507	0,731
80	0,485	0,449	0,512	0,688
100	0,494	0,505	0,517	0,660
150	0,508	0,515	0,523	0,620
Рейка	-	0,550	-	-

В зависимости от Z_v по табл. Находят Y и на изгиб рассчитывают зубья того из пары сцепляющихся колес, для которого произведение Y[σ]_F меньше.

1.9. Усилия, действующие в цилиндрическом косозубом зацеплении

Окружное усилие:

Радиальное усилие:

где α – угол зацепления, α= 20⁰

Осевое усилие:

2. Последовательность расчета конических передач

2.1. Определение диаметра колеса

Допускаемые контактные напряжения определяют также, как для цилиндрических колес.

При расчете конической передачи коэффициент нагрузки принимают равным K= 1,5 из-за консольного расположения конической шестерни.

Требуемый внешний делительный диаметр колеса из условия контактной прочности равен:

где M₁ – крутящий момент на валу шестерни, Нмм;

[σ]_H – допускаемое контактное напряжение, Н/мм²;

ϕ_Re – коэффициент ширины венца (при проектном расчете ϕ_Re ≤0,3);

K_П – коэффициент нагрузочной способности конических колес, для прямозубых колес K_П= 0,85, для косозубых колес K_П= 1,2…1,3.

Полученное значение d_e2 округляем до стандартного значения из ряда: 50; (56); 63; (71);80; 90; 100; (112); 125; (140); 160; (180); 200; (225); 250; 280; 315; 335; 400…

2.2. Определение числа зубьев шестерни и колеса

Число зубьев шестерни обычно назначают в пределах: Z₁= 18…20. Более точно число зубьев можно определить по данным табл. 15.

Таблица 15. Рекомендуемое минимальное число зубьев шестерни

U	Z1 при β
	0 - 15^0	20 - 25^0	30 - 40^0
1	17	17	17
2	13	12	11
> 3,15	12	10	8

Число зубьев колеса: Z₂=Z₁∙U

2.3. Определение внешнего (окружного) модуля передачи и фактического передаточного числа

Внешний окружной модуль конической передачи равен:

Полученное значение модуля m_te необходимо округлить до ближайшего стандартного значения (табл. ).

Уточняют фактическое передаточное число:

Отклонение полученного фактического передаточного числа от стандартного допускается в пределах ±3%.

2.4. Определение внешнего конусного расстояния и угла наклона зуба

Внешнее конусное расстояние (по принятому модулю m_te) равно:

Ширина венца b=ψ_Re∙R_e, мм

Уточняют угол β_m (средний угол наклона зуба на делительном конусе). Для этого сначала определяют β_e – наружный угол наклона зуба на делительном конусе по соотношению:

2.5. Определение углов делительных конусов и среднего окружного модуля

Углы делительных конусов:

Средний окружной модуль m_tm:

Средний нормальный модуль m_nm:

2.6. Проверка действительных контактных напряжений

Проверка действительных контактных напряжений выполняется после уточнения коэффициента нагрузки в зависимости от окружной скорости

где M₁ – крутящий момент на шестерне, Нмм;

b – длина зуба, мм.

Допускаемое отклонение действительных контактных напряжений от допускаемых должно находиться в пределах +5…- 20%. .

2.7. Определение действительных напряжений изгиба в конической паре

где P – окружное усилие, Н;

β_m – средний угол наклона зуба на делительном конусе;

b – ширина венца, мм;

y – коэффициент формы зуба; его принимают в зависимости от эквивалентного числа зубьев рассчитываемого колеса (рассчитываются зубья того колеса, для которого произведение y[σ]_F меньше):

– торцовый коэффициент перекрытия:

2.8. Расчет усилий в конической передаче

Окружное усилие

Осевое усилие на шестерне

Радиальное усилие на шестерне

3. Последовательность расчета червячных передач

3.1. Эквивалентное число циклов нагружения зубьев при расчете на контактную прочность

При n₁=n=const, M_max=M_н, для нашего случая эквивалентное число циклов нагружения зубьев шестерни

Эквивалентное число циклов нагружения для зубьев колеса

3.2. Эквивалентное число циклов нагружения зубьев при расчете на изгибную прочность

При n₁=n=const, M_max=M_н, для нашего случая

Эквивалентное число циклов нагружения для зубьев колеса

3.3. Расчет коэффициента долговечности для контактной прочности

Если , то принять K_HL=0,585.

3.4. Определение коэффициента долговечности при расчете на изгиб

Если , то принять K_FL=1,0.

3.5. Определение допускаемых напряжений

3.5.1. Допускаемые контактные напряжения

В червячных передачах червяки, как правило, изготавливают из стали, а венцы червячных колес из антифрикционных материалов: бронз, латуней, серого чугуна.

Допускаемые контактные напряжения (бронза или серый чугун) назначают в зависимости от принятого материала (табл. 16) и скорости скольжения V_s, которую предварительно необходимо определить по зависимости:

где n₁ – частота вращения червяка, мин^-1;

M₂ – крутящий момент червячного колеса, Нм.

Таблица 16. Материалы и допускаемые напряжения для червячных колес

Группа материала	Марка	Способ отливки	σв,МПа σu (для СЧ)	σT, МПа	Vs, м/с
Бронзы оловянистые	БрО10Н1Ф1	Ц	283	165	> 5
	БрО10Ф1	К/З	275/230	200/140
	БрО5Ц5С5	К/З	200/145	90/80
Бронзы безоловянистые и латуни	БрФ10Ж4Н4	Ц/К	700/650	460/430	2..3
	БрФ10Ж3Мц1,5	К/З	550/450	360/300
	БрФ9Ж3Л	Ц/К/З	530/500/425	245/230/195
	ЛЦ23А6Ж3Мц2	Ц/К/З	500/450/400	330/295/260
Чугуны серые 3	СЧ18	З	355	-	< 2
	СЧ15	З	315	-

Таблица 17. Допускаемые контактные напряжения, МПа

Материал	Твердость червяка
	HB≤350	HRC≥45
Группа 1	[σ]H=0,75σвKHLCv	[σ]H=0,9σвKHLCv
Группа 2	[σ]H=250-25Vs	[σ]H=300-25Vs
Группа 3	[σ]H=175-35Vs	[σ]H=200-35Vs

Примечание. C_v – коэффициент, учитывающий износ материала колес.

При расположении червяка вне масляной ванны значения [σ]_H следует уменьшить 15%.

3.5.2. Допускаемые напряжения изгиба

Допускаемые напряжения изгиба определяют по зависимостям, приведенным в табл. 18.

Таблица 18. Допускаемые напряжения изгиба, МПа

Материал	Передача
	нереверсивная	реверсивная
Группа 1, 2	[σ]F=(0,88σв+0,25σT)KFL	[σ]F=0,12σвKFL
Группа 3	[σ]F=0,12σuKFL	[σ]F=0,06σuKFL

3.6. Расчет межосевого расстояния и выборов основных параметров передачи

3.6.1. Определение числа заходов червяка и чисел зубьев червячного колеса

В силовых червячных передачах число заходов червяка назначают в пределах Z₁=1,2, 4, а число зубьев червячного колеса должно быть в пределах Z₂ = 27…80. Параметры Z₁ и Z₂ можно принимать по данным таблицы (табл. 19).

Таблица 19. Рекомендуемые значения Z₁ и Z₂ для нестандартных червячных передач

Передаточное число, U	Число заходов червяка, Z1	Число зубьев червячного колеса, Z2
7…8	4	28…32
9…13	3…4	27…52
14…24	2…3	28…72
25…27	2…3	50…81
28…40	1…2	28…80
40 и более	1	40 и более

3.6.2. Расчет межосевого расстояния

В червячных передачах на контактную прочность и изгиб рассчитываются зубья червячного колеса, как имеющие меньшую поверхностную и общую прочность. Расчет на контактную прочность должен обеспечить не столько отсутствие усталостного разрушения (выкрашивания) рабочей поверхности зубьев колеса, сколько отсутствие заедания, приводящего к задиру рабочих поверхностей.

где Z₂ – число зубьев червячного колеса;

q – коэффициент диаметра червяка (табл. );

K – коэффициент нагрузки, при симметричном расположении колес и червяка K=1,3; при несимметричном или консольном – K =1,5;

M₂ – крутящий момент на червячном колесе, Нмм;

[σ]_H – допускаемые контактные напряжения для материала червячного колеса, МПа.

Предварительно задаются величиной коэффициента диаметра червяка q из ряда 8, 10, 12,5 (обычно принимают q = 10).

3.6.3. Расчет стандартного модуля и проверка условия сборки

Стандартный осевой модуль равен:

Полученное значение модуля округляют до ближайшего стандартного значения (табл. 5).

По принятым стандартным значениям m и q уточняют межосевое расстояние (условие сборки):

Полученное значение межосевого расстояние должно точно соответствовать стандарту. При невозможности получить стандартное межосевое расстояние необходимо изменить совокупность стандартных параметров, ориентируясь на данные, приведенные в табл. 5, или выполнить корригирование червячного колеса.

Таблица 20. Основные параметры некорригированных цилиндрических червячных передач

aw	m (мм); q; z2; z1
40	1;16;64:1	2;10;30:1
50	1,25;16;64:1	2;12;38:1	2;12;38:2	2;12;38:4	2,5;10;30:1
63	1,5;16;68:1	3;10;32:1	3;10;32:2	3;10;32:4	4;9;31:1	4;9;32:2	4;9;32:4
80		2;16;64:1	2,5;12;52:1	2,5;12;52:2	2,5;12;52:4
100	2,5;16;64:1	4;10;40:1	4;10;40:2	4;10;40:4	5;9;31:1	5;9;31:2	5;9;31:4
140	3,5;12;68:1	5;10;46:1	5;10;46:2	5;10;46:4	7;9;31:1	7;9;31:2	7;9;31:4
160	4;12;68:1	5;10;54:1	5;10;54:2	5;10;54:4	8;8;32:1	8;8;32:2	8;8;32:4
180	4;14;76:1	4,5;12;68:1	6;10;50:1	6;10;50:2	6;10;50:4	9;9;32:1	9;8;32:2
200	5;12;68:1	10;8;32:1	10;8;32:2	10;8;32:4
225	4,5;16;84:1	6;12;63:1	9;8;42:1	9;8;42:2	9;8;42:4
250	5;16;84:1	10;8;42:1	10;8;42:2	10;8;42:4
280	7;12;68:1	8;12;58:1	8;12;58:2	8;12;58:4	10;10;46:1	10;10;46:2	10;10;46:4
280		14;8;32:1	14;8;32:2	14;8;32:4
315			7;12;78:1
400		10;12;68:1	16;8;42:1	16;8;42:2	16;8;42:4
450	10;12;78:1	12;10;65:1	18;8;42:1	18;8;42:2	18;8;42:4

3.7. Определение скорости скольжения и действительных контактных напряжений

Действительная скорость скольжения определяется по формуле:

Необходимо иметь в виду, что изменение скорости скольжения приводит к изменению допустимых контактных напряжений.

Действительные контактные напряжения равны:

где a_w - стандартное межосевое расстояние, мм;

M₂ – крутящий момент на колесе, Нмм.

Отклонение от допустимого значения контактных напряжений, скорректированные относительно действительной скорости скольжения, не должны превышать +5...-15%. В противном случае необходимо скорректировать величину стандартного межосевого расстояния.

3.8. Геометрические размеры червяка и червячного колеса

Геометрические размеры червячной передачи можно принимать по данным табл. 21.

Таблица 21. Геометрические размеры червячной передачи

Размеры червяка, мм	Размеры червячного колеса, мм
d1=mq	d2=mz1
dw1=mq	dw2=mz2
da1=m(q+2)	da2=m(z2+2)
df1=m(q+2)	df2=m(z2+2)
df1=m(q-2,4)	df2=m(z2+2,4)
b1= (табл. )	dam2, b2 (табл.)

Таблица 22. Длина нарезной части червяка b₁, ширина венца b₂ и наибольший диаметр червячного колеса d_aw2, мм

Коэффициент смещения, ξ	Число заходов червяка, Z1
	Z1=1	Z2=2	Z3=4
+ 0,5	b1≥(11+0,1Z2)m		b1≥(12,5+0,1Z2)m
0	b1≥(11+0,06Z2)m		b1≥(9,5+0,09Z2)m
- 0,5	b1≥(8+0,06Z2)m		b1≥(10,5+Z1)m
daw2	≤de2+2m	≤de2+1,5m	≤de2+m
b1	≤0,75da1		≤0,67da1

3.9. Проверка напряжений изгиба

Окружная сила в зацеплении:

где M₂ – крутящий момент на червячном колесе, Нмм.

Удельная окружная динамическая сила:

Расчетные напряжения изгиба зуба червячного колеса:

где Y_F – коэффициент формы зуба (табл. 23)

Таблица 23. Значение коэффициента Y_F, учитывающего форму зуба

и концентрацию напряжений в зубе червячного колеса

Z, (ZV)	YF
26	1,85
28	1,8
30	1,76
32	1,71
35	1,64
37	1,61
40	1,55
45	1,48
50	1,45
60	1,4
80	1,34
100	1,3
150	1,27
300	1,24

3.10. Силы, действующие в червячном зацеплении

Окружное усилие на червяке:

Окружное усилие на червячном колесе:

Радиальное усилие на червяке:

Радиальное усилие на червячном колесе:

Осевое усилие на червяке:

Осевое усилие на червячном колесе:

где α - угол зацепления, α = 20⁰;

ρ – угол трения, зависит от скорости скольжения V_s, ρ=arctgf, f – коэффициент трения, (табл. 24);

γ – угол подъема витков червяка, tgγ=Z₁/q .

Таблица 24. Зависимость коэффициента трения f от скорости скольжения V_s, м/с

(червяк стальной, колесо из оловянистой бронзы)

Vs, м/с	0,1	0,25	0,5		1,0		1,5
f	0,08-0,09	0,065-0,075	0,55-0,65		0,045-0,056		0,04-0,05
Vs, м/с	2	2,5	3	4		7	10
f	0,035-0,045	0,03-0,04	0,028-0,035	0,023-0,03		0,018-0,026	0,016-0,024

4. Последовательность расчета планетарных передач

4.1. Общие вопросы

Расчет на прочность планетарных передач ведут по формулам для цилиндрических зубчатых передач (раздел ). Расчет выполняют для каждого зацепления. Например, в передаче, изображенной на рис. Необходимо рассчитать внешнее зацепление колес 1 и 2 (солнечное колесо и сателлиты) и внутреннее – колес 2 и 3 (сателлиты и корончатое колесо). Так как модули и силы в этих зацеплениях одинаковы, а внутреннее зацепление по своим свойствам прочнее внешнего, то при одинаковых материалах колес достаточно рассчитать только внешнее зацепление.

Расчет ведут в последовательности, изложенной в разделе 1, с некоторыми особенностями, отмеченными ниже.

4.2. Расчет коэффициентов долговечности

При определении допускаемых напряжений коэффициенты долговечности K_HL и K_FL определяют по числу циклов N_экв изменения напряжений зубьев за весь срок службы при вращении колес только относительно друг друга.

Для солнечной (ведущей) шестерни ,

где n₁ – действительное число оборотов солнечной шестерни относительно стойки;

n_H – действительное число оборотов водила относительно стойки.

Для сателлитов или

где n₂ – действительное число оборотов сателлита относительно стойки;

n_H – действительное число оборотов водила относительно стойки;

Z₁ – число зубьев солнечной шестерни;

Z₂ – число зубьев сателлита.

4.3. Подбор чисел зубьев планетарной передачи

При расчете чисел зубьев планетарной передачи необходимо обеспечить условия соосности, сборки и соседства.

Условие соосности заключается в равенстве межосевых расстояний a_w зубчатых пар с внешним и внутренним зацеплением. Для некоррегированных колес:

поскольку в зацеплении участвуют колеса с одинаковым модулем, имеем:

Задаются числом зубьев солнечной (ведущей) шестерни из условия неподрезания ножки зуба, принимая для неё Z₁≥17. Число зубьев неподвижного корончатого колеса находят по формуле:

Полученные числа зубьев проверяют по условиям сборки и соседства.

Условие сборки требует, чтобы во всех зацеплениях центральных колес сателлитами имело место совпадение зубьев со впадинами, в противном случае собрать передачу невозможно. Установлено, что при симметричном расположении сателлитов условие сборки удовлетворяется, если сумма зубьев центральных колес (Z₁+Z₃) кратна числу сателлитов с =2…6 (обычно с = 3), т.е.

Условие соседства требует, чтобы сателлиты при вращении не задевали зубьями друг друга. Для этого необходимо, чтобы сумма радиусов вершин зубьев соседних сателлитов, равная d_a2=Z₂+2, была меньше расстояния определенного расстояния l:

где a_w=0,5m(Z₁+Z₂).

Из этого выражения следует:

4.4. Межосевое расстояние

Межосевое расстояние прямозубой планетарной передачи пары колес внешнего зацепления (солнечной шестерни с сателлитом) определяется зависимостью:

где u¹ – передаточное число рассчитываемой пары зубчатых колес, u¹=Z₂/Z₁;

K_c – коэффициент неравномерности распределения нагрузки между сателлитами, K_c= 1,1…1,2;

c – число сателлитов;

ψ_a – коэффициент ширины зуба, при u¹ ≤6,3 принимают ψ_a = 0,5, а при u¹ >6,3 ψ_a = 0,4.

Полученное значение a_w округляют до стандартного значения.

4.5. Определение геометрических параметров передачи и модуля зацепления

Ширину корончатого колеса принимают:

Ширину венцов сателлитов и солнечной шестерни принимают на 2…4 мм больше значения b₃.

Делительный диаметр солнечной шестерни:

Модуль зацепления:

Полученное значение модуля округляют до ближайшего стандартного значения, а затем уточняют числа зубьев колес по формулам:

с последующей проверкой условий сборки и соседства.

4.6. Окружная сила в зацеплении

Окружное усилие в планетарной передаче равно:

Радиальную силу определяют по известной зависимости

5. Расчет и конструирование вала

Расчет вала осуществляют в три этапа (ориентировочный расчет, расчет диаметра вала в опасном сечении и расчет на выносливость).

5.1. Ориентировочный расчет вала

Для выполнения ориентировочного расчета вала необходимо знать только величину крутящего момента, передаваемого валом. Наименьший диаметр вала равен (из расчета на чистое кручение):

где M₁ – крутящий момент, Нмм;

[τ] – допускаемое напряжение на кручение, МПа, рекомендуется принимать [τ] = 15…25 МПа.

Полученное значение диаметра вала необходимо округлить до ближайшего большего значения по нормальному ряду диаметров (по ГОСТ 8032): 16, 17, 18, 19, 20, 21, 22, 24, 25, 26, 28, 30, 32, 34, 36, 38, 40, 42, 45, 48, 50, 53, 56, 60, 63, 67, 70, 75, 80, 90, 100, 105, 110, 115, 120, 130, 140, 150, 160…

Имея значение минимального диаметра вала, переходят к его конструированию, т.е. определяют все диаметральные и линейные размеры вала. Диаметральные размеры вала:

Диаметр вала под подшипниками качения:

d_n1=d_в1+(3…5), мм (81)

Полученное значение диаметра вала под подшипника качения необходимо округлить до ближайшего большего значения из нормального рядя диаметром кратного 5 мм.

Диаметр вала под шестерней:

d_ш1=d_n1+(3…5), мм (82)

Максимальный диаметр вала (диаметр заготовки):

d_max1=d_ш1+(3…5), мм. (83)

Вместо расчета на кручение для предварительного определения диаметра валов иногда применяют эмпирические зависимости. В местах установки шестерни на быстроходный и промежуточный валы:

d_шБ≈0,22a_wБ; d_шП≈0,3a_wБ; (84)

Для тихоходного вала в месте посадки колеса:

d_kT≈0,3a_wT.

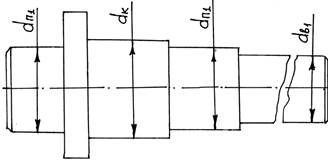
Рис.16

На рис. 16 представлен эскиз тихоходного вала зубчатого одноступенчатого редуктора с нанесенными диаметральными размерами.

Линейные размеры вала определяют по эмпирическим зависимостям или путем расчета. Длину выходного конца вала рекомендуется назначать в пределах:

Длину посадочной поверхности под шестерню или зубчатое колесо (шкив) назначают равной или большей ширины венца (обода шкива). Принятую длину посадочной поверхности согласуют с рассчитанной, исходя из прочности шпоночного (шлицевого) соединения:

где h – высота шпонки;

t – размер шпоночного соединения;

[σ]_см – допускаемое напряжение смятия, для стали [σ]_см - 100…120 МПа, для чугуна – 50…60 МПа.

Длину ступицы также согласуют с диаметром вала l_K1=0,8d_K. Если при расчете длины посадочной поверхности под колесо окажется, что её длина превышает 1,5d_K, то необходимо вместо шпоночного соединения применять шлицевое.

Длину посадочной поверхности под подшипник качения (l_П1) принимают равной ширине внутреннего кольца подшипника по каталогу.

Длину буртика вала ∆ между посадочными поверхностями подшипника и колеса принимают по конструктивным соображениям (обычно ∆≈4…8 мм). Диаметр поверхности для буртика принимают по размеру проката и, как правило, не обрабатывают.

Определив все размеры (рис. 16) вала переходят к его конструированию и составлению расчетной схемы вала.

5.2. Расчет диаметра вала в опасном сечении

Для выполнения второго этапа расчета вала необходимо иметь величины: крутящего момента; усилий, действующих в зубчатом зацеплении; усилий, действующих на вал со стороны механизма натяжения ременной или цепной передач; линейные размеры: расстояние между опорами вала, координаты точек приложения усилий в зацеплении и натяжения.

На основании этих данных составляется расчетная схема вала (двухопорная статически определимая балка), на которую прикладываются все внешние силы. Определяются реакции опор и строятся эпюры изгибающих и крутящего момента. На рис. 17 - 27 приведены схемы нагружения типовых валов редукторов.

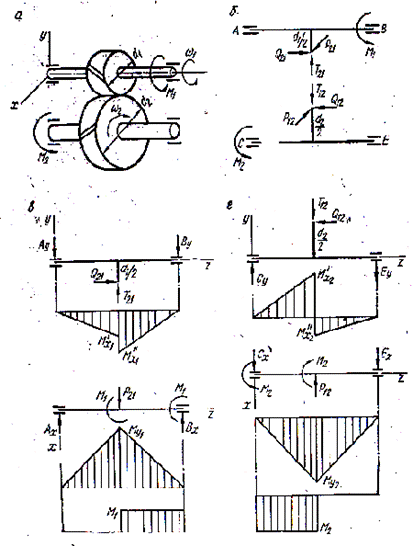
Рис. 17. Цилиндрическая косозубая одноступенчатая передача: а – схема передачи; б – усилия в зацеплении;

в – схемы нагружения ведущего вала в двух взаимно перпендикулярных плоскостях, эпюры изгибающих моментов

в этих плоскостях и эпюра крутящих моментов; г – то го же ведомого вала

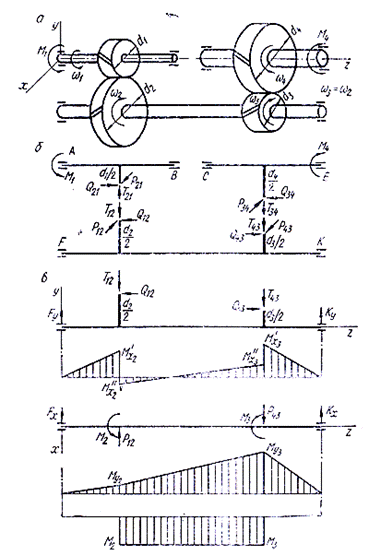
Рис. 18. Цилиндрическая косозубая двухступенчатая соосная передача: а – схема передачи; б – усилия в зацеплении;

в – схемы нагружения ведущего вала в двух взаимно перпендикулярных плоскостях, эпюры изгибающих моментов в этих плоскостях и эпюра крутящих моментов

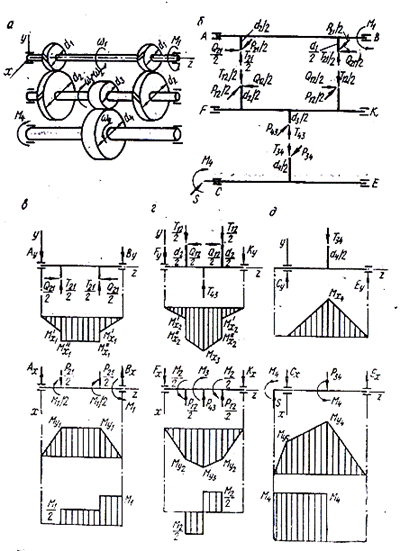
Рис. 19. Цилиндрическая косозубая двухступенчатая развернутая передача: а – схема передачи; б – усилия в зацеплении;

в – схемы нагружения ведущего вала в двух взаимно перпендикулярных плоскостях, эпюры изгибающих моментов в этих плоскостях и эпюра крутящих моментов

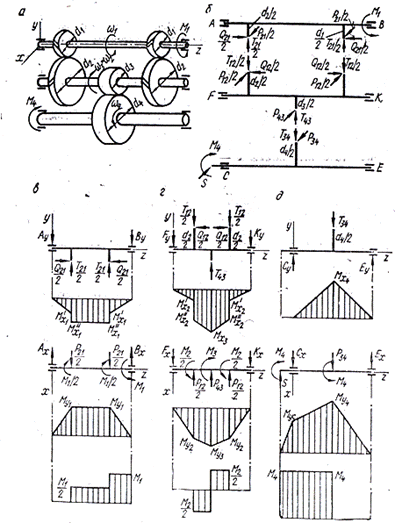
Рис. 20. Цилиндрическая передача с первой раздвоенной косозубой и второй прямозубой ступенями: а – схема передачи; б – усилия в зацеплении;

в – схемы нагружения ведущего вала в двух взаимно перпендикулярных плоскостях, эпюры изгибающих моментов в этих плоскостях и эпюра крутящих моментов;

г – то же для промежуточного вала; д – то же для ведомого вала

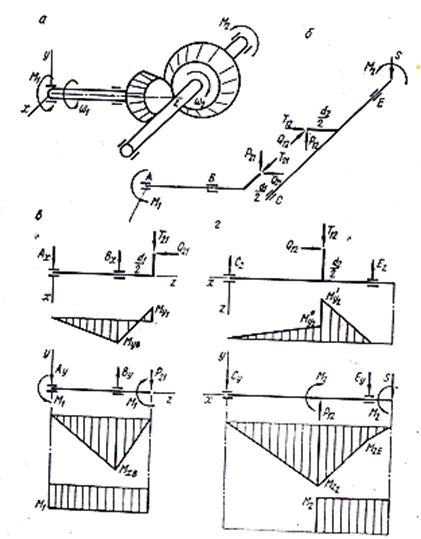
Рис. 21. Коническая прямозубая одноступенчатая передача: а – схема передачи; б – усилия в зацеплении;

в – схемы нагружения ведущего вала в двух взаимно перпендикулярных плоскостях, эпюры изгибающих моментов в этих плоскостях и эпюра крутящих моментов;

г – то же для промежуточного вала

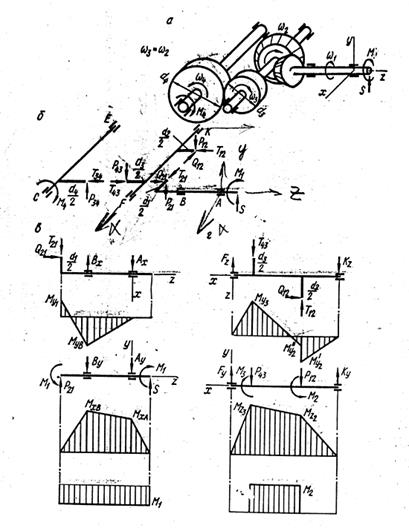
Рис. 22. Коническо-цилиндрическая двухступенчатая прямозубая передача: а – схема передачи; б – усилия в зацеплении;

в – схемы нагружения ведущего вала в двух взаимно перпендикулярных плоскостях,

эпюры изгибающих моментов в этих плоскостях и эпюра крутящих моментов; г – то же для промежуточного вала

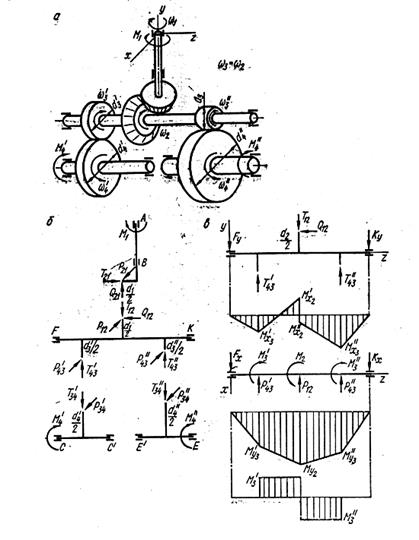
Рис. 23. Коническо-цилиндрическая двухступенчатая двухпоточная прямозубая передача: а – схема передачи; б – усилия в зацеплении;

в – схемы нагружения ведущего вала в двух взаимно перпендикулярных плоскостях, эпюры изгибающих моментов в этих плоскостях и эпюра крутящих моментов

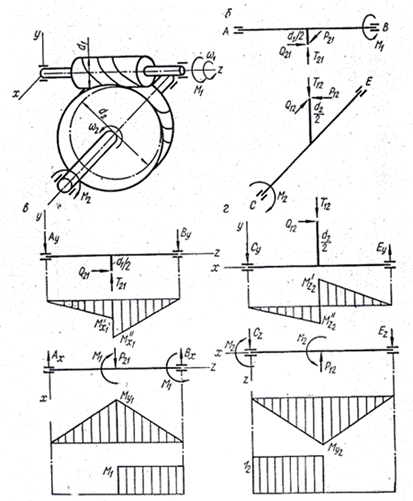
Рис. 24. Червячная передача: а – схема передачи; б – усилия в зацеплении; в – схемы нагружения ведущего вала в двух взаимно перпендикулярных

плоскостях, эпюры изгибающих моментов в этих плоскостях и эпюра крутящих моментов; г – то же для промежуточного вала

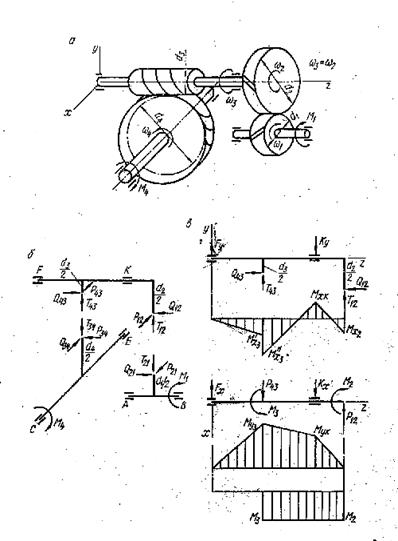
Рис. 25. Зубчато-червячная передача с первой цилиндрической косозубой ступенью: а – схема передачи; б – усилия в зацеплении;

в – схемы нагружения ведущего вала в двух взаимно перпендикулярных плоскостях, эпюры изгибающих моментов в этих плоскостях и эпюра крутящих моментов

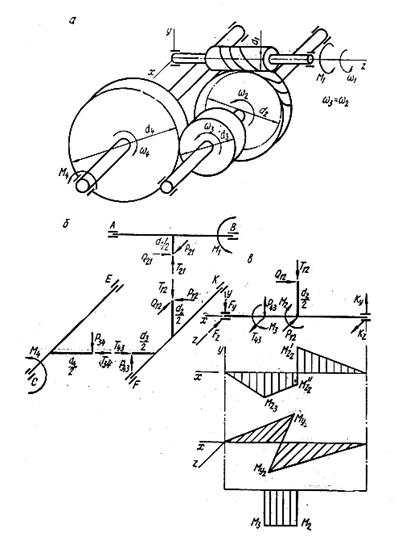
Рис. 26. Червячно-зубчатая передача со второй цилиндрической прямозубой ступенью: а – схема передачи; б – усилия в зацеплении;

в – схемы нагружения ведущего вала в двух взаимно перпендикулярных плоскостях, эпюры изгибающих моментов в этих плоскостях и эпюра крутящих моментов

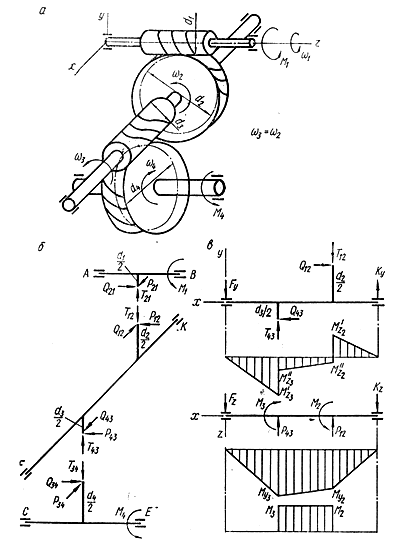
Рис. 27. Двухступенчатая червячная передача: а – схема передачи; б – усилия в зацеплении; в – схемы нагружения ведущего вала в двух

взаимно перпендикулярных плоскостях, эпюры изгибающих моментов в этих плоскостях и эпюра крутящих моментов

По форме эпюр определяют расположение опасного сечения, а минимальное значение диаметра вала в этом сечении находят по зависимости:

где M_пр – приведенный момент в опасном сечении, МПа;

[σ]_u – допускаемое напряжение при изгибе, принимают [σ]_u ≈50…60 МПа.

Приведенный момент M_пр в соответствии с теорией наибольших касательных напряжений рассчитывают по зависимости:

Проводят анализ полученного результата. Может оказаться, что диаметр вала в опасном сечении d_оп больше диаметра вала в этом сечении, полученному в результате компоновки d_K. Это означает, что в эскизе вала необходимо увеличить диаметр вала под колесом не менее, чем d_оп.

Если диаметр вала в опасном сечении d_оп оказался меньше, чем d_K, то диаметр вала под колесом d_K можно оставить без изменения.

5.3. Расчет вала на сопротивление усталости (выносливость)

Опыт эксплуатации показывает, что для валов основной причиной выхода из строя является усталостное разрушение и поэтому для валов расчет на сопротивление усталости является одним из основных.

Для проведения усталостного расчета необходимо следующее: рабочий чертеж вала, вид нагружения (реверсивное или нереверсивное), силовые факторы (крутящий момент, вид и величина действующих в исследуемом сечении переменных напряжений), материал и термическая обработка вала, виды и расположение концентраторов напряжений, шероховатость поверхностей.

Расчет выполняют в форме проверки коэффициента запаса прочности S, который должен удовлетворять неравенство:

где S_σ – коэффициент запаса по нормальным напряжениям изгиба;

S_τ - коэффициент запаса прочности по касательным напряжениям кручения;

[S] – допустимый коэффициент запаса усталостной прочности, выбирается в пределах 1,5…2,5 для отрасли машиностроения.

Коэффициент запаса по нормальным напряжениям изгиба:

где σ_-1 и τ_-1 – пределы выносливости материала вала, ориентировочно предел выносливости для конструкционных сталей равен:

K_σD и K_τD – суммарные коэффициенты, учитывающие влияние всех факторов на сопротивление усталости соответственно при изгибе и кручении:

K_σ и K_τ – эффективные коэффициенты концентрации напряжений (отношение предела усталости, полученного в результате испытаний гладких образцов, к пределу усталости, полученному на образцах с концентраторами напряжений) соответственно при изгибе и кручении;

ε – коэффициент влияния абсолютных размеров поперечного сечения – масштабный фактор (отношение предела усталости образцов и деталей реальных размеров к пределу усталости, полученному при испытаниях стандартных образцов малых диаметров);

K_F – коэффициент влияния шероховатости поверхности;

K_V – коэффициент влияния упрочнения, вводимый для валов и осей с поверхностным упрочнением (закалка ТВЧ – цементация, азотирование и т.п.);

σ_a и σ_m – амплитудные и средние напряжения при изгибе;

τ_a и τ_m – амплитудные и средние напряжения при кручении;

ψ_σ и ψ_τ – коэффициенты чувствительности материала к асимметрии цикла напряжений соответственно при изгибе и кручении.

Для оценки выносливости вала в целом необходимо выполнить проверку коэффициента запаса прочности для нескольких характерных участков вала (например, в опасном сечении, в месте установки полумуфты или шкива ременной передачи, в местах нарезания шпоночных пазов и т.п.). Только при выполнении во всех этих сечениях условия (89) можно говорить об удовлетворении усталостной прочности всего вала.

Если в сечении имеются два концентратора напряжений, то в расчет принимается наибольший из них. При отсутствии в сечении одного из видов нагружения (изгиба) коэффициент запаса прочности в этом сечении приравнивается к частному коэффициенту запаса прочности по действующим напряжениям (S=S_τ).

5.4. Справочные данные по коэффициентам концентрации напряжений

Галтель (рис. 28) K_σ и K_τ в зависимости от отношений t/r, r/d и от предела прочности материала приведены в табл. 25.

Выточка (рис. 28). Значения K_σ и K_τ приведены в табл. 26.

Поперечное отверстие (рис. 28). Значения K_σ и K_τ, вычисленные по отношению к сечению нетто в зависимости от d/d₀ и σ_в, приведены в табл. 25.

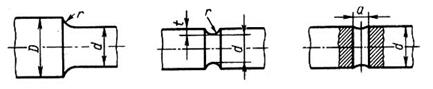
а) б) в)

Рис. 28. Концентраторы напряжений: а) галтель; б) выточка; в) поперечное отверстие.

Таблица 25. Эффективные коэффициенты концентрации напряжений в ступенчатом переходе с галтелью

t/r	r/d	Kσ, при σв, МПа				Kτ , при σв, МПа
		500	700	900	1200	500	700	900	1200
1	0,01	1,35	1,4	1,45	1,5	1,3	1,3	1,3	1,3
	0,02	1,45	1,5	1,55	1,6	1,35	1,35	1,4	1,4
	0,03	1,65	1,7	1,8	1,9	1,4	1,45	1,45	1,5
	0,05	1,6	1,7	1,8	1,95	1,45	1,45	1,5	1,55
	0,10	1,45	1,55	1,65	1,85	1,4	1,4	1,45	1,5
2	0,01	1,55	1,6	1,65	1,7	1,4	1,4	1,45	1,45
	0,02	1,8	1,9	2,0	2,15	1,55	1,6	1,65	1,7
	0,03	1,8	1,95	2,05	2,25	1,55	1,6	1,65	1,7
	0,05	1,75	1,9	2,0	2,2	1,55	1,6	1,65	1,75
3	0,01	1,9	2,0	2,1	2,2	1,55	1,6	1,65	1,75
	0,02	1,95	2,1	2,2	2,4	1,6	1,7	1,75	1,85
	0,03	1,95	2,1	2,25	2,45	1,65	1,7	1,75	1,9
5	0,01	2,1	2,25	2,35	2,5	2,2	2,3	2,4	2,6
	0,02	2,15	2,3	2,45	2,65	2,1	2,15	2,25	2,4

Таблица 26. Эффективные коэффициенты концентрации напряжений для валов с выточкой

Напряженное состояние	σв, МПа	При отношении r/d
		0,01	0,02	0,03	0,05	0,10	0,01	0,02	0,03	0,05
Изгиб (Kσ)		При отношении t/r= 0,5					При отношении t/r =1,0
	500	1,95	1,85	1,75	1,65	1,5	2,15	2,05	1,95	1,85
	700	2,05	1,95	1,85	1,75	1,55	2,25	2,15	2,1	1,95
	900	2,15	2,05	1,95	1,9	1,6	2,4	2,3	2,2	2,1
	1200	2,3	2,2	2,1	2,05	1,75	2,6	2,5	2,35	2,25
		При отношении t/r = 2,0					При отношении t/r = 5,0
	500	2,35	2,25	2,15	-	-	2,45	2,35	-	-
	700	2,5	2,4	2,3	-	-	2,65	2,5	-	-
	900	2,65	2,5	2,4	-	-	2,8	2,65	-	-
	1200	2,85	2,7	2,6	-	-	3,05	2,85	-	-
Кручение (Kτ)	500	1,7	1,6	1,5	1,4	1,2	-	-	-	-
	700	1,9	1,75	1,65	1,5	1,25	-	-	-	-
	900	2,1	1,95	1,8	1,65	1,3	-	-	-	-
	1200	2,4	2,2	2,05	1,8	1,4	-	-	-	-

Таблица 27. Эффективные коэффициенты концентрации для валов в месте поперечного отверстия

𝜎в, МПа	Kσ при d0/d		Kτ при d0/d = 0,05…0,25
	0,05…0,10	0,15…0,25
≤700	2,0	1,8	1,75
900	2,15	1,9	1,9
≥1000	2,3	2,1	2,0

Шпоночная канавка, значения K_σ и K_τ вычисляются по отношению к сечению нетто, приведены в табл. 28. Значения K_σ соответствует одной шпоночной канавке, выполненной торцевой фрезой, и значения K_τ - двум шпоночным канавкам, но данные таблицы можно использовать как для расчета валов с одной, так и с двумя канавками.

Шлицевые валы. Значения K_σ и K_τ приведены в табл. 28. Расчет шлицевых валов следует вести по сечению нетто; расчет на кручение – по внутреннему диаметру, так как выступы принимают весьма малое участие в передаче крутящего момента.

Таблица 28. Эффективные коэффициенты концентрации напряжений для шлицевых, шпоночных и резьбовых участков валов

𝜎в, МПа	Kσ для шлицев	Kτ для прямобочных шлицев	Kτ для эволь- вентных шлицев	Kσ для валов со шпонками	Kτ для валов со шпонками	Kσ для резьбы
500	1,45	2,25	1,43	1,6	1,4	1,8
600	1,55	2,36	1,46	1,75	1,5	1,95
700	1,60	2,45	1,49	1,9	1,7	2,2
800	1,65	2,55	1,52	2,05	1,9	2,3
900	1,70	2,65	1,55	2,2	2,0	2,45
1000	1,72	2,7	1,58	2,3	2,2	2,6

Значения коэффициента влияния абсолютных размеров поперечного сечения ε приведены в табл. 29.

Таблица 29. Значение коэффициента влияния абсолютных размеров ε

в зависимости от диаметра вала

Напряженное состояние	Материал	Значение ε при диаметре вала, мм
		15	20	30	40	50	70	100	200
Изгиб	Сталь углеродистая	0,95	0,92	0,88	0,85	0,81	0,76	0,70	0,61
Изгиб, кручение для всех сталей	Высокопрочная легированная сталь	0,87	0,83	0,77	0,73	0,7	0,65	0,59	0,52

Шероховатость. Значения коэффициента влияния шероховатости поверхности приведены в табл. 30. С повышением прочности стали растут требования к микрогеометрии поверхности. При грубой обработке поверхности предел выносливости высокопрочных сталей оказывается не выше, чем у обычных сталей.

Поверхностные упрочнения являются мощным средством повышения выносливости валов. При поверхностных упрочнениях повышается прочность наиболее напряженного поверхностного слоя и в нем создаются остаточные напряжения сжатия. Коэффициенты влияния упрочнения приведены в табл. 31.

Таблица 30. Значение коэффициента влияния шероховатости поверхности K_F

Механическая обработка поверхности	Среднее арифметическое отклонение профиля Ra, мкм	Значение коэффициента KF при σв, МПа
		400	600	1200
Шлифование	0,32…0,08	1	1	1
Обточка	2,5…0,32	1,05	1,10	1,25
Обдирка	20…5	1,2	1,25	1,5
Необработанная поверхность с окалиной и т.д.	-	1,35	1,5	2,2

Таблица 31. Значение коэффициента влияния упрочнения K_V при поверхностной обработке

Вид упрочнения	Образец
	без концентрации напряжений	с концентрацией напряжений*
Закалка ТВЧ углеродистых и легированных сталей	1,2…1,5	1,5…2,5
Азотирование при глубине слоя 0,1…0,4 мм	1,1…1,15	1,3…2,0
Цементация при толщине слоя 0,2…0,6 мм	1,1…1,5	1,2…2,0
Обкатка роликами углеродистых и легированных сталей	1,1…1,25	1,3…1,8
Обдувка дробью углеродистых и легированных сталей	1,1…1,2	1,1…1,5

* Большие значения при большей концентрации напряжений

5.5. Рекомендации по оформлению рабочего чертежа вала

Рабочий чертеж вала является документом, по которому его изготавливают, поэтому он должен содержать исчерпывающую информацию по геометрии вала, его механической и термической обработке, технических требованиях на изготовление.

Геометрическая форма вала должна обеспечивать наличие индивидуальных посадочных поверхностей для каждой сопрягаемой детали, отсутствие существенных концентраций напряжений. Механическая обработка должна обеспечивать получение заданной конструктором классов шероховатости, обеспечивающих надежную работу изделия.

Термическая обработка вала должна обеспечивать расчетные прочностные характеристики материала вала и его отдельных поверхностей. Технические требования должны исключать возможность нарушения технологии изготовления вала и облегчать контроль за его изготовлением.

Чертеж вала должен выполняться на ватмане (формат А4 или А3) в полном соответствии с правилами ЕСКД. На поле чертежа вала должны быть выполнены сечения по шпоночным пазам. На посадочные поверхности вала должны быть нанесены стандартные посадки, определены и нанесены базы для обработки и допуски на отклонение формы и взаимного расположения наиболее важных поверхностей.

На рис. 29-31 показаны примеры выполнения рабочих чертежей некоторых валов, применяемых в редукторах.

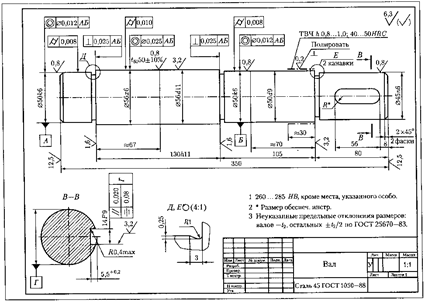
Рис. 29. Пример выполнения вала

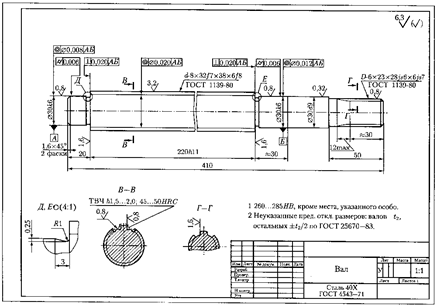
Рис. 30. Пример выполнения вала

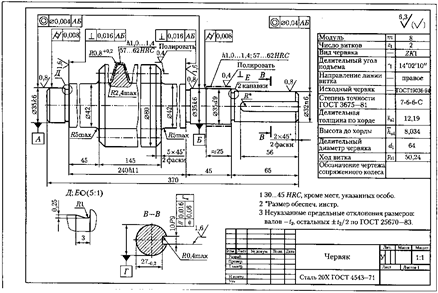
Рис. 31. Пример выполнения червяка

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Строительная механика Теория машин и механизмов

00:00:00