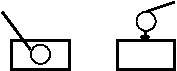Главная
Лабораторная
работа
Строение
и структурный анализ механизмов
1. Цель работы
- Усвоить основные понятия и определения теории
механизмов и машин.
- Ознакомиться с простейшими видами механизмов и названиями
их звеньев.
- Научиться определять какие схемы кинематических
цепей являются схемами механизмов.
- Научиться по моделям строить
структурные схемы простейших плоских механизмов, определять степень подвижности
их и выделять группы Ассура.
2.
Теоретические положения
2.1
Основные понятия и определения
Звено – одно или несколько жестко соединенных твердых
тел, входящих в состав кинематической цепи (механизма).
Кинематическая
пара –
подвижное соединение двух соприкасающихся звеньев, допускающее вполне
определенное движение относительно друг друга.
Кинематическая
цепь –
система звеньев, связанных между собой кинематическими парами.
Механизм – такая кинематическая цепь, в которой при
заданном движении одному или нескольким звеньям относительного любого из них,
все остальные звенья совершают однозначно определяемые движения.
Плоскими
механизмами называются такие, точки
звеньев которых описывают траектории, лежащие в параллельных плоскостях.
Кинематические звенья, кинематические пары,
кинематические цепи и механизм изображают графически, используя рекомендуемые
обозначения (таблица 1).
Звенья механизмов делятся на подвижные
и неподвижные. Неподвижное звено
называют стойкой. На рисунке 1 стойка обозначена цифрой ноль (0).
Входное звено – звено, которому сообщается движение, преобразуемое
механизмом в требуемые движения других звеньев. На схемах входному звену
задается движение стрелкой: звено 1 на рисунке
1, а, б, в;
звено 8
на рисунке 1, г; звено
10 на рисунке 1, д.
Выходное
звено – звено, совершающее движение,
для выполнения которого создается механизм: звенья 3,
5, 7, 9, 11
на рисунке 1.
Таблица 1. Условные обозначения пар и звеньев
механизмов
|
Условное обозначение |
Названия изображения. Комментарий |
|
|
Стержень, рычаг, ось, вал, шатун и т.п. (звено). |
|
|
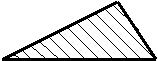
Звено в форме треугольника. Базисное звено. |
|
|
Соединение стержней – жесткое. Каждое представляет собой одно звено. |
|
|
Поступательно движущееся звено: ползун или камень кулисы. |
|
|
Вращательная
кинематическая пара. |
|
|
Соединение ведущего звена со стойкой вращательной парой А. |
|
|
Поступательно
движущееся звено, состоящее
из двух жестко соединенных деталей. |
|
|
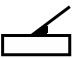
Шарнирное соединение стержня с
поступательно движущимся звеном. |
|
|
Ползун в направляющих: а и б
– направляющие (неподвижные) охватывают ползун. Ползун охватывает направляющую – в. |
|
а) б) в) |
Камень кулисы:
а и б
– камень кулисы охватывает кулису; в
– кулиса охватывает камень кулисы. |
|
|
Фрикционный механизм. |
|
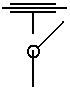
|
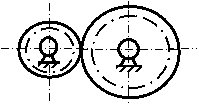
Наличие окружности, выполненной штрих-пунктиром, обозначает,
что на схеме представлен зубчатый механизм. |
|
|
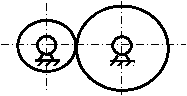
Варианты обозначения зубчатых
механизмов состоящих из двух цилиндрических колёс внешнего
зацепления. |
Кривошип – звено, совершающее полный оборот вокруг неподвижной
оси (рисунок 1, а, б, в).
Камень кулисы – звено, поступательно
движущееся относительно подвижной направляющей (звено 2, рисунок 1, а).
Кулиса – подвижная направляющая поступательной кинематической
пары (звено 3, рисунок 1, а), которая соединена со стойкой (звено
1, рисунок 1).
Шатун – звено, совершающее сложное плоско-параллельное
движение и не имеющее кинематических пар со стойкой (звено 4, рисунок 1, б).
Ползун – звено, образующее со стойкой поступательную пару
(звено 5, рисунок 1, б).
Коромысло – звено, совершающее колебательные движения
относительно неподвижной оси (звено 7, рисунок 1, в).
Кулачок – звено, которое выполнено в виде поверхности переменной
кривизны (звено 8, рисунок 1, г).
Толкатель – звено кулачкового механизма, взаимодействующее с
рабочей поверхностью кулачка и совершающее поступательное движение (звено 9,
рисунок 1, г).
Шестерня – зубчатое колесо с меньшим числом зубьев (меньшего диаметра)
по сравнению с другим зацепляющимся с ним зубчатым
колесом (на рисунке 1, д,
шестерня 10, зубчатое колесо 11).
Названия рычажным механизмам дают по входному и
выходному звеньям. На рисунке 1, а
«кривошипно-кулисный механизм», «кривошипно-ползун-ный»
(рисунок 1, б). Название механизма на рисунке 1, д соответствует конструктивному исполнению
звеньев в виде тел вращения с нарезанными зубьями – «зубчатый механизм», на
рисунке 1, г – «кулачковый механизм».
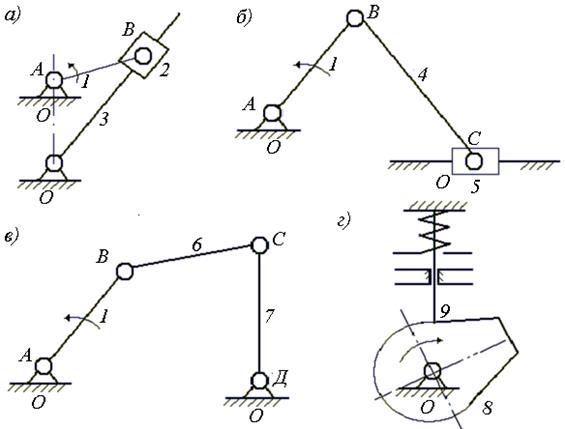
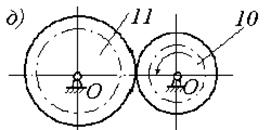
Рис. 1. Схемы механизмов
2.2. Классификация кинематических пар
Любая кинематическая пара ограничивает
движение звеньев, эти ограничения называют связями.
Кинематические пары классифицируют по следующим
признакам:
По числу
связей, налагаемых на относительное
движение их звеньев. Класс кинематической пары определяется числом связей.
По форме
контакта соприкасающихся звеньев: по
поверхности – такие кинематические пары называются низшими; по линии или в
точке – высшими.
По виду
относительного движения для каждого
из образующих ее звеньев:
обратимые кинематические пары реализует один и тот же вид
движения для каждого звена (кинематические пары III, IV, V классов);
необратимые кинематические пары (I, II классов)
реализуют разные виды движения для каждого звена образующих их.
2.3. Структурный анализ
Степень подвижности плоских механизмов определяется по
формуле Чебышева:
W=3n-2p5-p4, (1)
где n – число
подвижных звеньев механизма;
p5 – число
кинематических пар пятого класса;
p4 – число
кинематических пар четвертого класса.
В основе структурной теории лежат два понятия:
механизм первого класса и структурная группа (группа Ассура).
Механизмом
первого класса или начальным механизмом –
условно названо входное звено, соединенное со стойкой кинематической парой V класса,
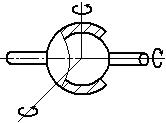
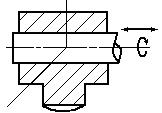
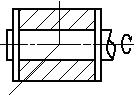
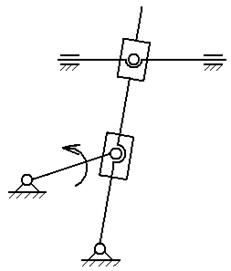
вращательной или поступательной (рисунок 2) .
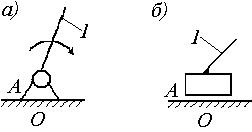
Рис. 2. Механизмы первого класса
Таблица 2. Кинематические пары и их условные
обозначения
|
Рисунок |
Условные обозначения |
Число степеней свободы |
Класс пары |
Название и тип пары |
||||||
|
|
|
5 |
I |
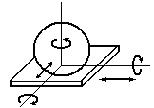
Шар - плоскость. Высшая. |
||||||
|
|
|
4 |
II |
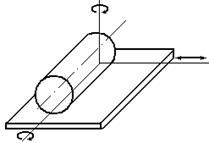
Цилиндр – плоскость. Высшая. |
||||||
|
|
|
3 |
III |
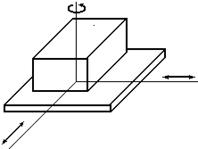
Плоскостная. Трёхподвижная. Низшая. |
||||||
|
|
|
3 |
IV |
Сферическая. Низшая. |
||||||
|
|
|
2 |
IV |
Цилиндрическая. Низшая. |
||||||
|
|
|
1 |
V |
Цилиндрическая. Низшая. |
||||||
|
|
|
1 |
V |
Поступательная. Низшая. |
Структурной
группой или группой Ассура называют кинематическую цепь с нулевой степенью
подвижности, причем такая группа не должна распадаться на
более простые, удовлетворяющие этому условию.
Класс структурной группы с числом звеньев больше двух равен числу кинематических пар, входящих в
замкнутый контур, образованный внутренними кинематическими парами. Группа,
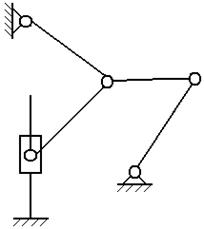
состоящая из двух звеньев и трех кинематических пар (рисунок 3, пары В, С, Д),
условно отнесена к группе второго класса
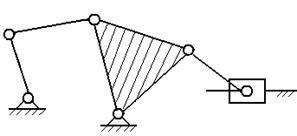
(2 кл.). На рисунке 4
изображена группа третьего класса
(3 кл.). Кинематические пары С, Д, Е
образуют замкнутый контур.
Порядок
структурной группы соответствует
числу свободных элементов кинематических пар, с помощью которых группу можно
присоединить к начальному механизму, стойке или звеньям других групп. На
рисунке 3 группа второго порядка (2 п.), на рисунке 4 группа
третьего порядка (3 п.).
Большинство рычажных механизмов состоят из структурных групп второго класса, которые называют диадами.
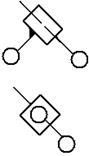
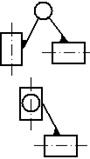
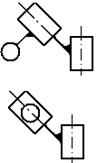
В таблице 3 приведены пять модификаций (видов) таких
групп, в которых вращательные пары заменяются поступательными.
Таблица 3. Структурные группы второго класса второго
порядка
|
Модификация группы |
Первая |
Вторая |
Третья |
Четвертая |
Пятая |
|
Изображение |
|
|
|
|
|
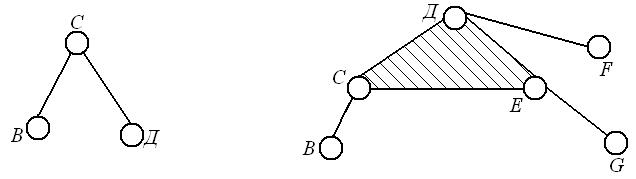
Рис.3. Группа Ассура 2 кл., 2 п. Рис. 4. Группа Ассура 3 кл., 3 п.
Класс
механизма соответствует классу
наивысшей группы, входящей в его состав.
Разложение кинематической цепи механизма на
структурные группы и начальные механизмы называют структурным анализом.
Структурный анализ проводят в следующем порядке:
- отсоединение начинают со структурных групп наиболее удаленных от
ведущего звена;
- в первую очередь стремятся отделять самые простые
группы – диады;
- следить за тем, чтобы степень подвижности
кинематической цепи механизма до и после отделения каждой структурной группы
оставалась неизменной;
- кинематическая пара и звено могут входить только в
одну структурную группу или начальный механизм.
Если в подвижное соединение входят более двух звеньев,
то число кинематических пар равно числу звеньев минус единица.
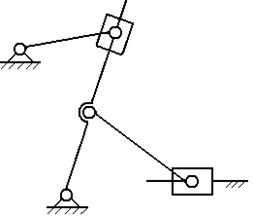
На рисунке
5 в соединение B входят пять звеньев, число кинематических пар
равно 5 – 1 = 4
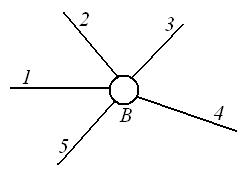
Рис. 5. Подвижное соединение
Графическое изображение механизма при помощи условных
обозначений звеньев и кинематических пар без соблюдения масштаба, называют структурной схемой механизма.
3.
Описание объекта исследования, приборов и инструментов
Для проведения
лабораторной работы, используют действующие модели плоских рычажных механизмов
с низшими парами пятого класса, модели кулачковых и зубчатых механизмов,
имеющих высшие кинематические пары четвертого класса.
Объектом исследования являются модели механизмов:
кривошипно-кулисные, кривошипно-ползунные, кривошипно-коромысловые, кулачковые,
зубчатые.
4.
Методика проведения исследований и обработка результатов
4.1. Ознакомиться с
моделями механизмов, изучить их структуру, найти ведущее звено. Определить
число подвижных звеньев в механизме, число, вид и класс кинематических пар,
последовательность присоединения звеньев друг к другу.
4.2. Начертить структурную схему механизма, пользуясь
таблицей 1, пронумеровать звенья, обозначить буквами кинематические пары.
4.3. Заполнить таблицу 4 – характеристика
кинематических пар.
4.4. Заполнить таблицу 5 – характеристика звеньев
механизма.
4.5. Определить степень подвижности механизма по
формуле 1.
4.6. Выполнить структурный анализ. Написать формулу
образования механизма, которая пишется в виде дроби. В числителе указываются
номера звеньев, в знаменателе – класс и порядок выделенной группы. Пример
оформления в приложении А.
Таблица 4 – Характеристика кинематических пар
|
Условное обозначение |
Вид движения (вращательное или поступательное) |
Тип (высшая или низшая) |
Класс пары |
|
А
– В
– … |
|
|
|
Таблица 5 – Характеристика звеньев механизма
|
Номер звена |
Название звена |
|
0 1 2 |
|
5.
Содержание и оформление отчета
5.1 Титульный
лист.
5.2 Цель
работы.
5.3 Схема исследуемого
механизма.
5.4 Таблицы 4 и
5.
5.5 Структурный
анализ исследуемого механизма (приложение А).
5.6 Схема и
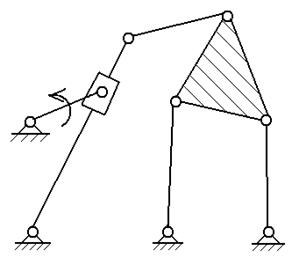
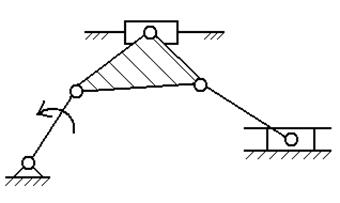
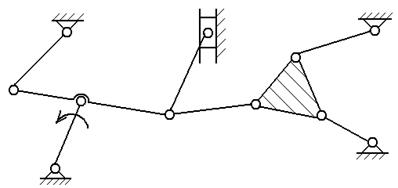
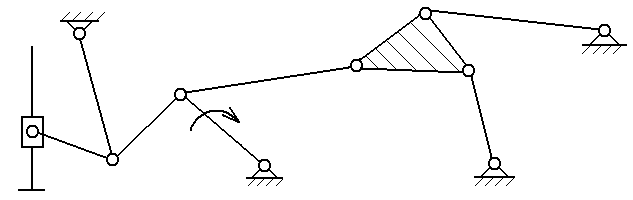
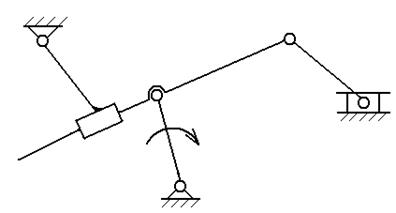
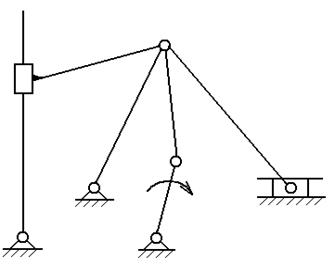
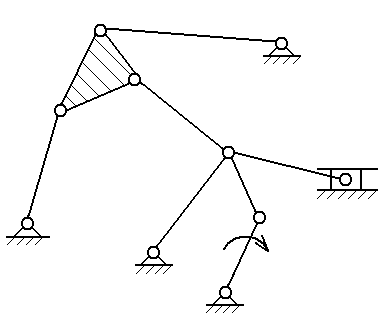
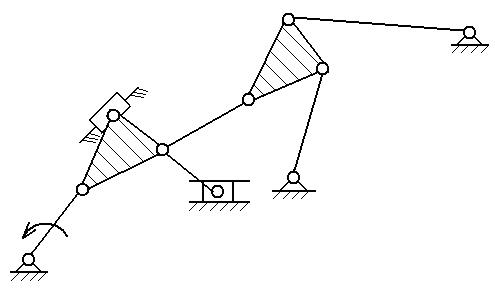
структурный анализ механизма заданного преподавателем из приложения Б.
6. Вопросы для
самоконтроля
1. Дайте определение понятия: «звено», «кинематическая
пара», «кинематическая цепь», «механизм».
2. По каким
признакам классифицируют кинематические пары?
3. Перечислите
виды кинематических цепей.
4. Какая
существует зависимость между числом степеней свободы и числом связей,
накладываемых кинематической парой.
5. Как
определяется класс кинематической пары?
6. Какую
кинематическую цепь называют механизмом?
7. Укажите
различия между структурной и кинематической схемами механизма.
8. Перечислите
виды рычажных механизмов.
9. Перечислите
виды механизмов.
10. Какое звено механизма
называют: «кривошипом», «шатуном», «коромыслом», «ползуном», «камнем кулисы»,
«кулисой», «стойкой»?
11. Какие
механизмы называют рычажными?
12. Дайте
характеристику кинематическим цепям, у которых степень подвижности W = 0; W= 1.
13. Дайте
определение понятия «структурная группа или группа Ассура».
14. Напишите
формулу Чебышева.
15. Изобразите
механизм 1 класса.
16. Изобразите
структурную группу 2 класса 2 порядка.
17. Изобразите
структурную группу 3 класса 3 порядка.
18. Как
определяются класс и порядок структурной группы (группы Ассура)?
19. Как
определяется класс механизма?
20. Составьте
формулу образования механизма.
21. Укажите
последовательность выполнения структурного анализа механизма.
22. Изобразите
простую кинематическую цепь.
23. Изобразите
сложную кинематическую цепь.
Приложение А (справочное)
Пример
оформления отчета
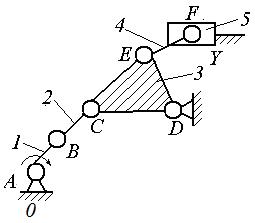
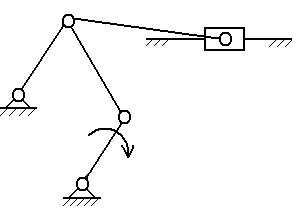
Рис.1. Структурная схема механизма
Степень подвижности механизма
W=3n-2p5-p4=3∙5-2∙7-0=1,
где n = 5; p5= 7; p4 = 0
Структурный анализ
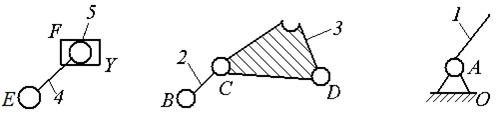
2 кл., 2 п. 2 кл.,
2 п.
1 кл.
W=3n-2p5-p4 W=3n-2p5-p4= W=3n-2p5-p4=
=3∙2-2∙3-0=0 =3∙2-2∙3-0=0 =3∙1-2∙1-0=1
Механизм 2 класса.
Формула образования механизма
![]()