Главная

Лабораторная работа

Определение параметров и размеров зубчатых колес

1. Цель работы

- Ознакомление с основными геометрическими параметрами и размерами цилиндрических колес с прямыми зубьями, а также с методами их измерения.

2. Теоретические положения

2.1 Общие сведения

Поверхности взаимодействующих зубьев колес должны обеспечить постоянство передаточного числа (U = const). Для выполнения этого условия боковые профили зубьев сопрягаемых колес должны подчиняться требованиям, вытекающим из основной теоремы зацепления: общая нормаль n-n, проведенная через точки касания профилей, делит расстояние между центрами колес O₁O₂ на части, обратно пропорциональные угловым скоростям (рис. 1). Математически теорема зацепления имеет вид:

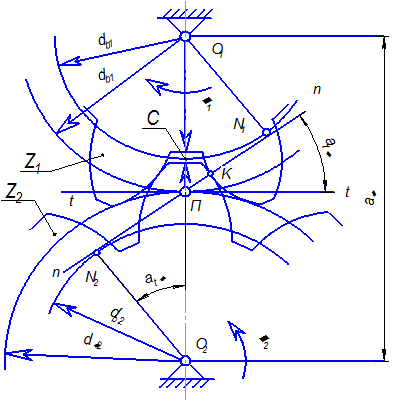
Рис. 1. Зацепление эвольвентных зубчатых колес

Из возможных профилей зубьев, удовлетворяющих основной теореме зацепления, наибольшее применение получило эвольвентное зацепление благодаря технологичности и достаточно высокой несущей способности. Эвольвента окружности образуется точкой К на прямых N₁K и N₂K при качении их без скольжения по окружностям с диаметрами dв₁ и dв_{2 .} Эти окружности называются основными. Линия N₁ N₂, по которой перемещается общая точка контакта К профилей зубьев при вращении колес – линия зацепления. Угол между линией зацепления и прямой t-t, перпендикулярной к межосевой линии O₁O₂ называется углом зацепления . Для колес без смещения угол зацепления .

При вращении зацепляющихся зубчатых колес окружности радиусов О₁П и О₂П перекатываются одна по другой без скольжения. Данные окружности называются начальными, их диаметр d_ω1 и d_ω2. Эти окружности являются сопряженными, т.е. понятие начальных окружностей относится только к паре колес находящихся в зацеплении. При изменении межосевого расстояния О₁ О₂ диаметры начальных окружностей изменяются.

Делительная окружность принадлежит отдельному колесу и получается при его зацеплении со стандартной рейкой. Окружность, являющаяся начальной при зацеплении с рейкой – делительная; её диаметр обозначается d (рис. 2). Для колес без смещения делительные окружности совпадают с начальными. Толщина зуба по делительной окружности S равна ширине впадины между двумя зубьями е.

Расстояние между двумя одноименными профилями соседних зубьев по делительной окружности – окружной шаг зацепления P. На делительной окружности шаг зацепления Р равен сумме толщины зуба S и ширины впадины между двумя зубьями е. Расчетная величина, равная отношению окружного шага зубьев Р по делительной окружности к числу π - окружной модуль зацепления

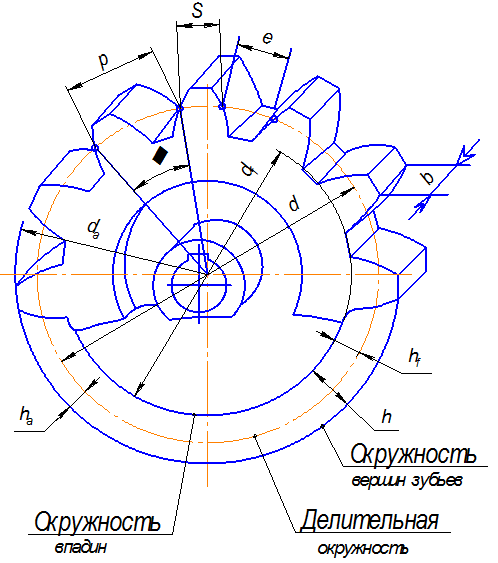
Рис. 2. Геометрические параметры цилиндрического колеса с прямыми зубьями

Модули зубьев зубчатых колес стандартизованы [табл. 1]. Диаметр делительной окружности выраженный через модуль равен:

где z- число зубьев зубчатого колеса.

Окружность, ограничивающая высоту зубьев – окружность вершин зубьев; её диаметр обозначается d_a. Окружность, ограничивающая глубину впадин, – окружность впадин зубьев, её диаметр обозначается d_f.

Таблица 1

Ряды предпочтительных чисел	Модуль зацепления m, мм
1-й ряд	1	1,25	1,5	2	2,5	3	4	5	6	8	10	12	16
2-й ряд	1,125	1,375	1,75	2,25	2,75	3,5	4,5	5,5	7	9	11	14	18

В зубчатых колесах расстояние между двумя соседними профилями зубьев, измеренное по нормали n-n (рис. 3), равно шагу P_в по основной окружности (длине дуги). Из треугольника О радиус основной окружности равен

0,5d_в = 0,5∙dcosα_ω;

шаг по основной окружности будет равен

P_в = Pcosα_ω.

Исходя из этого, шаг по основной окружности можно определять не длиной дуги, а расстоянием между двумя соседними зубьями по нормали (эвольвентными участками профиля зуба). Этот отрезок нормали представит развертку основной окружности и будет равен шагу P_в по основной окружности.

Основные параметры и размеры зубчатого колеса:

z – число зубьев колеса;

m – модуль зацепления;

α_ω - угол зацепления (для колес с нормальным исходным контуром α_ω=20°);

h_a=m – высота головки зуба;

h_f=1,25∙m – высота ножки зуба;

p – окружной шаг зацепления (по делительной окружности);

p_в - шаг зубьев по основной окружности;

S, S_в –толщина зубьев соответственно по делительной и основной окружности;

x- коэффициент смещения.

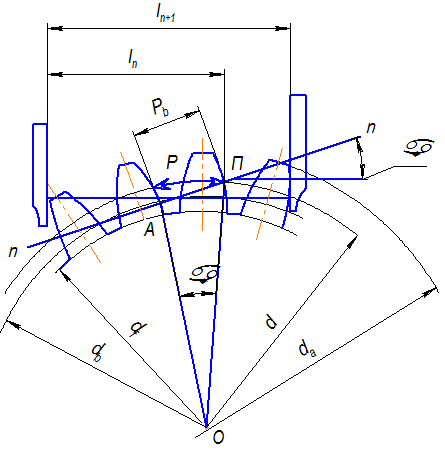
Рис. 3. Измерение шага зацепления по основной окружности колеса

3. Описание объекта исследования, приборов и инструментов

Для проведения лабораторной работы, используют действующие модели зубчатых механизмов, штангензубомер.

4. Методика проведения исследований и обработка результатов

4.1. Подсчитать число зубьев колеса.

4.2. По таблице 2 принять число зубьев колеса n, которые нужно охватить губками штангенциркуля, чтобы измерение было выполнено в пределах эвольвентной части профиля зуба.

Таблица 2

Число зубьев колеса Z	12-18	19-27	28-36	37-45	46-54	55-63	64-72	73-80
Измеряемое число зубьев n	2	3	4	5	6	7	8	9

4.3. Охватив штангенциркулем n зубьев колеса, измерить размер l_n между ними, затем, охватив штангенциркулем на 1 зуб больше, измерить размер l_n+1 между n+1 зубам. Полученные значения занести в таблицу 3.

Примечание. Каждый замер делается три раза на любых участках зубчатого колеса. Расчеты проводятся по средним значениям.

4.4. Определить расчетное значение модуля зацепления:

4.5. Полученное значение модуля зацепления округлить до ближайшего стандартного значения m (табл. 1).

4.6. Определить геометрические размеры зубчатого колеса, занеся полученные значения в табл. 4.

4.7. Измерить штангенциркулем диаметры выступов d_a и впадин d_f зубьев колеса, занеся полученные значения в табл. 5. Размеры d_a и d_f при четном числе зубьев Z измеряются штангенциркулем непосредствен, как показано на рис. 4,а. При нечетном числе зубьев Z сначала измеряется диаметр отверстия колеса d_отв, а затем расстояние от отверстия до окружности вершин l_а и до окружности впадин l_f зубьев (рис. 4,б), при этом диаметры вершин и впадин зубьев получаются суммированием диаметра отверстия и расстояния от отверстия до соответствующей окружности зуба.

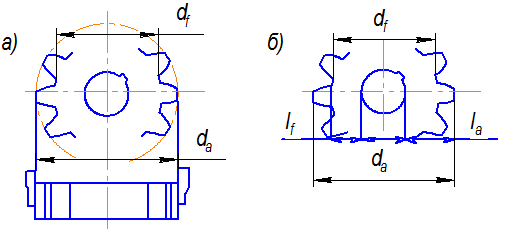
Рис. 4. Измерение диаметров выступов и впадин зубчатого колеса:

а – при четном; б – при нечетном числе зубьев

4.8. Зубчатое колесо может быть нарезано со смещением исходного контура режущего инструмента. В этом случае определить значение коэффициента смещения исходного контура:

Примечание. Коэффициент смещения может быть как положительным, так и отрицательным. В дальнейших расчетах подставляется в формулы с полученным знаком. Если значение коэффициента смещения получается близким к нулю, то принимается x=0.

4.9. Определить толщину зуба по делительной окружности (рис. 2), мм:

4.10. Определить половину центрального угла зуба по дуге делительной окружности (рис. 5), град:

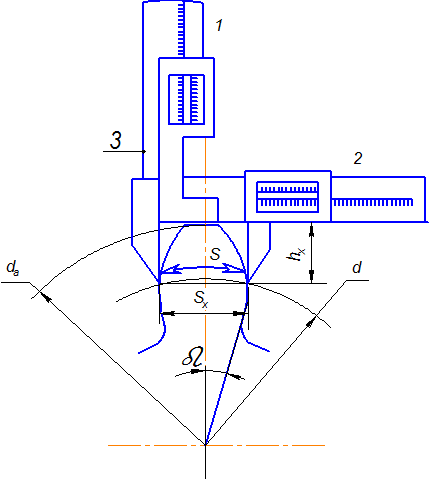
Рис. 5. Измерение толщины зуба по хорде делительной окружности

4.11. Определить радиальное расстояние от окружности вершин зубьев до измеряемой хорды по делительной окружности, мм:

где d_a, d –диаметры, соответственно вершин зубьев и делительной окружности принимаются по табл. 4.

4.12. Определить толщину зуба по хорде делительной окружности, мм:

4.13. Измерить штангензубомером толщину зуба по хорде делительной окружности S_xизм. (рис. 5). Полученное значение S_xизм сравнить с расчетным значением S_x.

Примечание: штангензубомер имеет две шкалы 1 и 2 с нониусами. Шкала 1 служит для замера радиального расстояния h_x от окружности головок зубьев до измеряемой хорды, шкала 2 служит для замера толщины зуба по хорде. По шкале 1 перемещается установочная пластина 3. До начала замера установочную пластину 3 фиксируем на расстоянии h_x. Для этого на шкале 1 устанавливаем радиальное расстояние до измеряемой хорды на дуге делительной окружности. Устанавливаем штангензубомер на зуб так, чтобы пластина 3 упиралась в вершину зуба, сдвигаем губки штангензубомера до касания их с боковыми поверхностями зуба и по шкале 2 определяем хордальную толщину зуба S_xизм.

5. Содержание и оформление отчета

Определение параметров и размеров зубчатых колес.

1. Цель работы.

2. Эскиз зубчатого колеса с основными размерами.

3. Таблица 3 замеров шага зубьев по основной окружности зубчатого колеса.

Таблица 3

Номер замера	Расстояние между n зубьями ln , мм	Расстояние между (n+1) зубом ln+1, мм	Измерение значение шага зубьев по основной окружности Pвиз=ln+1-ln, мм
1
2
3
Среднее значение	lnср	Ln+1 ср	Pв ср

4. Определение геометрических размеров зубчатого колеса табл. 4.

Таблица 4

№ n/n	Геометрический размер зубчатого колеса	Расчетная формула
1	Шаг зубьев по делительной окружности	p=π∙m
2	Шаг зубьев по основной окружности	pв=π∙m∙cosαω
3	Диаметр делительной окружности	d=mz
4	Диаметр основной окружности	dв=d∙cosαω
5	Диаметр вершин (головок) зубьев	da=d+2m
6	Диаметр впадин (ножек) зубьев	df=d-25m
7	Толщина зуба по основной окружности	Sв=ln+1-n∙Pв

5. Таблица замеров диаметров выступов и впадин зубьев колеса.

Таблица 5

Номер замера	Диаметры вершин da и впадин df зубьев
	Четное число Z зубьев колеса		Нечетное число Z зубьев колеса
	da, мм	df, мм	dотв, мм	la, мм	lf, мм	da=dотв+2la	df=dотв+2lf
1
2
3
Среднее значение	da ср	df ср	dотв ср	la ср	lf ср	da ср	df ср

6. Определить коэффициент смещения X и окружную толщину зуба по делительной окружности S.

7. Определить и измерить толщину зуба по хорде делительной окружности S_x.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Строительная механика Теория машин и механизмов

00:00:00