Главная

Раздел 2. Усталость и выносливость деталей машин

Содержание

Характеристики цикла при переменных напряжениях в деталях машин

Усталость деталей машин, ее природа и процесс разрушения

Предел выносливости материалов

Местные напряжения в деталях машинах

Режимы работы и расчетные нагрузки машин

Определение коэффициента внешней динамики К_А

Выводы и рекомендации

Вопросы для самопроверки

Характеристики цикла при переменных напряжениях в деталях машин

Многие детали машин или их элементы, такие, как валы, зубья зубчатых колес и другие, работают в условиях, когда возникающие в них напряжения периодические изменяют свое значения или значение и знак.

По характеру изменения во времени нагрузки в машинах делят на постоянные и переменные.

Статическое нагружение вызывает в материале детали постоянное напряжение, которое не изменяется в течение длительного времени ни по величине, ни по направлению.

Постоянные нагрузки могут вызывать переменные напряжения. Так, при вращении вала, нагруженного изгибающим моментом, один и те же волокна его оказываются попеременно то в растянутой, то в сжатой зоне. Так же поочередный вход в зацепление зубьев колес вызывает в них изменение напряжений.

Причиной изменения напряжений может быть и переменный характер действия внешней нагрузки. Переменность нагрузки, например, автомобиля может связана: с загрузкой (автомобиль может ехать с полной загрузкой, с частичной или без груза), с рельефом местности (езда под гору, по ровной местности, в гору), с видом и качеством дорожного полотна или грунта (грунтовая дорога, асфальт, булыжная мостовая), с остановом и разгоном у светофора, с квалификацией водителя и т.д. Каждый из этих факторов может изменять нагрузку в несколько раз.

Переменные нагрузки вызывают переменные напряжения. Детали, длительное время подвергающиеся повторно-переменной нагрузке, разрушаются при напряжениях значительно меньших предела прочности материала при статическом нагружении. Как показывает статистика, около 80% поломок и аварий, происходящих при эксплуатации машин, вызвано усталостными явлениями (цикличными нагрузками). Циклические нагрузки наиболее явно выражены в машинах и механизмах с возвратно-поступательным движением звеньев (поршневые машины, кулачковые механизмы). Однако и в механизмах вращательного движения циклические нагрузки неизбежны (зубчатые передачи, валы).

Характеристикой напряженности детали является цикл напряжений - совокупность последовательных значении напряжений σ за один период при регулярном нагружении. В случае действия касательных напряжении τ остаются в силе все приведенные ниже термины и соотношения с заменой σ на τ. Продолжительность одного цикла нагружения называют периодом и обозначают Т (рис.1). Напряжения с одним максимумом и одним минимумом в течение одного периода при постоянстве параметров цикла называют регулярным нагружением.

Цикл переменных напряжении характеризуют (рис.1):

1. максимальным напряжением σ_max;

2. минимальным напряжением σ_min;

3. средним напряжением цикла σ_m=0,5(σ_max+σ_min);

4. амплитудой цикла σ_a=0,5(σ_max-σ_min);

5. коэффициентом асимметрии цикла R=σ_min/σ_max;

6. характеристикой цикла ρ=σ_a/σ_m, , 0<ρ<∞.

7. коэффициентом амплитуды a=σ_a/σ_max.

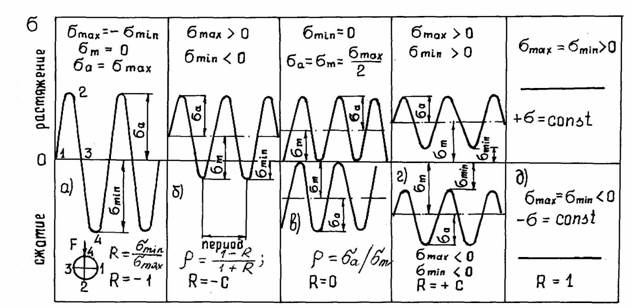
Рис.1

Если R=0 (σ_min= 0; σ_m=σ_a=0,5σ_max; ρ=1; а=0,5), то имеем отнулевой цикл напряжений (рис.1, в). Пульсирующее нагружение в соответствии с отнулевым циклом (когда напряжения изменяются от нуля до максимума) имеют: зубья зубчатых колес при работе в одну сторону, толкатели и шатуны тихоходных механизмов с малой нагрузкой холостого хода, нереверсивные валы (напряжения кручения).

Если R=-1 (σ_m=0; σ_a=σ_max; ρ=∞; а=1), то цикл напряжений называется симметричным (рис.1, а). Этот цикл является наиболее неблагоприятным для работы детали, так как характеризуются изменением не только значения, но и знака действующих напряжений (знакопеременный цикл). Здесь наибольшие и наименьшие напряжения противоположны по знаку и одинаковы по модулю (напряжения изгиба при вращении валов и осей).

Если R=1 (σ_a=0; σ_max=σ_min=σ_m=σ; ρ=0; а=0), действуют постоянные статические напряжения.

Во всех других случаях - циклы напряжения асимметричные (рис.1, б, г), , ; -1<R<+1; (-1; -0,5; 0; +0,5; +1); ∞≤ρ<0; 1≤a≤0.

В случае переменных касательных напряжений остаются в силе все приведенные выше термины и соотношения с заменой σ на τ.

Число циклов нагружения, которые материал выдерживает до разрушения, зависит от максимального напряжения и амплитуды цикла. По мере уменьшения напряжений число циклов до разрушения детали увеличивается и при некотором достаточно малом напряжении становится неограниченно большим. Это напряжение называют пределом выносливости и кладут в основу расчета деталей машин, подверженным циклическим нагрузкам.

Предел выносливости для отнулевого цикла обозначают индексом «0» (σ₀ ; τ₀), для симметричного цикла – «-1» (σ_-1 ; 𝜏_-1), то есть коэффициент асимметрии цикла «r» сопровождает обозначение предела выносливости (σ_r ; τ_r).

Рассмотрим определение числа циклов нагружения на примере вала, подверженного действию изгибающего момента и вращающегося с частотой вращения n, мин^-1 (угловой скоростью ω, с^-1).

Продолжительность одного цикла изменения напряжения, т.е. период Т, с:

T=2π/ω=60/n

Общее число циклов за промежуток время L_h, ч:

N=3600∙L_h/T=573∙ω∙L_h=60∙n∙L_h.

Усталость деталей машин, ее природа и процесс разрушения

В процессе эксплуатации машин на детали действуют пульсирующие или циклические нагрузки, напряжение от которых вызывает усталостные разрушения. Опыты показывают, что эти детали длительное время подвергавшиеся действию переменных напряжений, разрушаются при напряжениях, значительно меньших, чем временное сопротивление σ_в (иначе предел прочности).

Разрушение при циклическом нагружении происходит вследствие возникновения микротрещин в зоне концентрации напряжений. Трещины постепенно развиваются, проникая вглубь, поперечное сечение деталей ослабляется и в некоторый момент происходит мгновенное разрушение.

Под усталостью понимают процесс постепенного накопления повреждений материала под действием переменных напряжений, приводящих к изменению свойств, образования трещин, их развитию и разрушению. Свойство материала противостоять усталости называется выносливостью.

Необходимо отметить, что усталость металла отличается от биологической усталости, если у живого организма во время отдыха усталость восстанавливается, то у детали повреждения в процессе усталости накапливаются и являются необратимыми. Процесс носит сложный характер. Проблему усталости и прочности сформулировал американский проф. Джон Коллинз:

1. Оценка долговечности менее точна, чем расчеты на прочность.

2. Усталостные характеристики не могут быть получены из механических свойств, их необходимо измерять непосредственно.

3. Для подтверждения требуемой долговечности необходимо проведение испытаний прототипа конструкции.

4. Материалы и конфигурации конструкции должны подбираться из условий обеспечения медленного распространения трещин и возможности обнаружения их до достижения или опасных размеров.

5. Результаты разных тождественных испытаний могут отличаться друг от друга, и это требует статистической обработки.

6. Для достижения требуемой надежности приходится применять концепцию «безопасного повреждения» конструкции. Это означает, что даже разрушение какого-либо элемента конструкции не нарушит работоспособности в течение некоторого непродолжительного периода времени.

Многолетние исследования усталостных повреждений позволяют сделать вывод, что усталость охватывает две значительно отличающиеся друг от друга области циклического нагружения и деформирования. В первом случае при циклическом нагружении возникают значительные пластические деформации. Эта область называется малоцикловой усталостью, и число циклов не превышает 10⁴…10⁵.

Другая область – циклическое нагружение, при котором деформация во время каждого цикла в значительной степени упруга. Для этой области характерны малые напряжения (нагрузки) и большое число циклов до разрушения. Эта область называется многоцикловой усталостью и характеризуется долговечностью более 10⁶ …10⁷ циклов.

На рис. 2 показано разрушение вала малоуглеродистой пластичной стали в изложении проф. Дж. Коллинза, где 1 – начало разрушения, 2 – шероховатая поверхность, 3 – гладкая поверхность, 4 – радиальные усы, 5 – область среза; а – малая относительная скорость роста трещины; b – большая относительная скорость распространения трещины; с – конечная стадия разрушения.

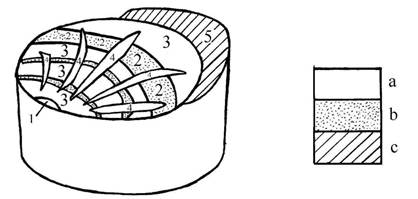
Рис. 2. Разрушение вала из малоуглеродистой стали

Теперь рассмотрим характерную особенность усталостного излома шейки коленчатого вала по трактовке проф. В. П. Когаева показанного на рис. 3.

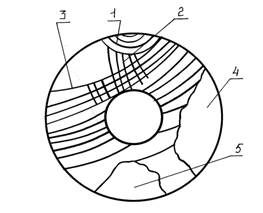
Рис. 3. Усталостный излом шейки коленчатого вала

Здесь 1 – локальная зона, в которой возникает начальная микроскопическая трещина усталости. Место, где начинается ее развитие, называется фокусом излома. Малую зону, прилегающую к фокусу излома и соответствующую начальной макроскопической трещине усталости, называют очагом разрушения. При больших уровнях переменных напряжений могут быть несколько фокусов и очагов разрушения. Чаще всего фокус и очаг разрушения располагаются у поверхности детали, где бывают дефекты и возникают наибольшие напряжения.

Далее образуются ступеньки и рубцы 2, при слиянии параллельных трещин, развивающихся из нескольких очагов. Отмечают на изломе участки развития трещины, на котором видны усталостные линии 3, являющиеся следами фронта продвижения трещины с гладкой блестящей поверхностью.

После распространения усталостной трещины на большую часть поперечного сечения происходит ускоренное развитие трещины 4 и долом 5. Зона долома 5 носит характер хрупкого разрушения и имеет шероховатую поверхность.

Как видим из рис. 2 и 3, объяснения механизма разрушения научных школ США и России имеют общность и некоторые отличия.

Таким образом, усталость является одним из видов разрушения с переменными амплитудами напряжений при эксплуатации машин со случайным спектром нагружения. Кривые усталости строятся при постоянной амплитуде напряжения для каждой точки, поэтому конструктору необходимо иметь теорию или гипотезу, подтвержденную экспериментально.

К настоящему времени предложено много гипотез накопления повреждении. Первая гипотеза была предложена в 1924 году А. Пальмгреном и развита Майнером, которая называется правилом линейного суммирования повреждении (рис. 4).

Рис. 4. Зависимость поврежденности при усталости D_i/D_𝚺 от относительного числа циклов n_i/N_𝚺

Согласно кривой усталости при действии напряжения с постоянной амплитудой σ₁ полное разрушение произойдет через N₁ циклов. В результате действия напряжения σ₁ с числом циклов n₁ (n₁< N₁) произойдет частичное повреждение, которое характеризуется числом D₁. Воздействие спектра различных уровней напряжений приводит к поврежденности D_i для каждого уровня напряжения σ_i из этого спектра. При этом предполагается, что полное разрушение произойдет, если

D₁+D₂+D₃+…+D_i-1+D_i≥1

Гипотеза А. Пальмгрена утверждает, что доля поврежденности при любом уровне амплитуды напряжения цикла σ₁ прямо пропорциональна отношению числа циклов его действия к полному числу циклов, т.е.

D_i=n_i/N_i. (1)

Тогда

Эти соотношения (1) и (2) представляют собой формулировку гипотезы Пальмгрена или правила линейного суммирования повреждений.

Достоинство – простота, а недостаток - не учитывает очередности воздействия напряжений различных уровней и предлагает одинаковую скорость накопления повреждений.

Если произвести лабораторные испытания с напряжениями двух уровней σ₁>σ₂, то суммы Σn_i/N_i в порядке очередности будут значительно отличаться. Для возрастающей последовательности напряжений сумма Σn_i/N_i будет больше единицы, а для убывающей – меньше единицы. Таким образом, экспериментальные суммы в момент разрушения колеблются в пределах от 0,25 до 4 в зависимости от порядка прикладывания циклических напряжений. Если различные амплитуды напряжений изменяются по нормальному закону, по мнению Д.Н. Решетова или квазислучайному закону, по мнению Дж. Коллинза, то экспериментальные суммы Σn_i/N_i в момент разрушения приблизятся к единице. Вообще n в этом случае суммы колеблются от 0,6 до 1,6 (рис. 4).

Как показывают эксперименты, напряжение с возрастающей амплитудой вызывает больше повреждения, чем такие же циклы напряжений, расположенные в порядке убывания амплитуд. В этой связи, кроме гипотезы Пальмгрена, имеются гипотезы Марко – Старки, Марина, Мэнсона, Генри, Гатса, Кортена – Долана и другие.

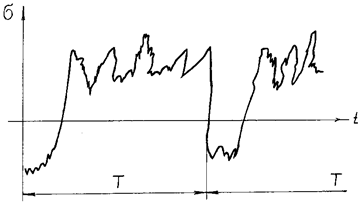
Рис. 5. Пример квазислучайной зависимости напряжения от времени

Принято считать, что процесс усталостного разрушения состоит из трех фаз. Первая фаза – возникновение трещины, вторая – распространение трещины и, наконец, трещина достигнет критического размера и процесс разрушения завершает третья фаза – быстрый неустойчивый рост трещины до полного разрушения. Моделирование всех фаз не завершено.

Таким образом, расчеты на долговечность и надежность следует считать приближенным, и носят они вероятностный характер.

Предел выносливости материалов

Для расчетов на прочность при повторно – переменных напряжениях требуется знание механических характеристик материала. Их определяют испытанием на сопротивление усталости серии стандартных тщательно отполированных образцов на специальных машинах. Наиболее простым является испытание на изгиб при симметрическом цикле напряжений.

Задавая образцам различные значения напряжений σ_max, определяют число циклов N, при котором произошло их разрушение. По полученным данным строят кривую σ_max- N, называемую кривой усталости. Если данную кривую построить в логарифмических координатах, то приобретает вид прямой (рис.6). Как видно из рис.6,а при малых напряжениях образец, не разрушаясь, может выдержать очень большое число циклов нагружения.

Кривые усталости показывают, что:

– разрушающее напряжение в области малых N близко к показателям статической прочности;

– по мере увеличения N величина разрушающих напряжений уменьшается и при некотором числе циклов стабилизируется;

– ордината горизонтального участка кривой усталости является пределом выносливости.

Для большинства конструкционных сталей предел выносливости определяют при 10⁶…10⁷ циклов. Эти значения и берут за базу испытаний. Для цветных металлов, например алюминия, даже при числе циклов 10⁷…10⁸ наблюдается дальнейшее медленное падение разрушающего напряжения. В этом случае говорят об ограниченном пределе выносливости (обычно это 5∙10⁷).

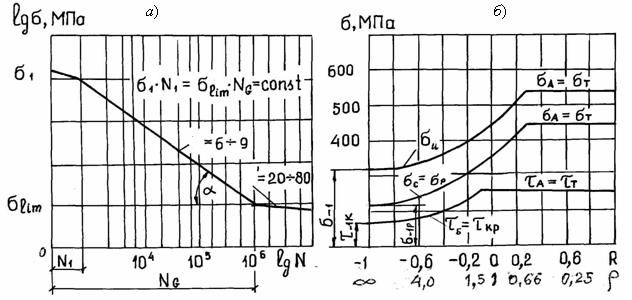
Рис.6

Впервые натурные испытания осей железнодорожных вагонов были проведены с 1857 года по 1870 год Августом Вёлером на изгиб, кручение и осевое нагружение. Кривая выносливости Вёлера показанная на рис.7 присуща для деталей из сплавов цветных металлов. Постоянство показателя кривой выносливости сохраняется вплоть до очень малого уровня напряжения. Поэтому введено понятие условный предел выносливости и базовое число циклов.

Рис.7. Кривая выносливости Вёлера

Условным пределом выносливости 𝛔_lim или пределом ограниченной выносливости называется наибольшее максимальное напряжение, при котором не происходит разрушение, когда осуществляется определенное число циклов, принятое за базу – N_lim=N_G=N₀.

В логарифмических координатах уравнение соответствует прямой линии с показателем кривой выносливости q=8÷15 для гладких образцов при симметричном цикле.

Для конструкционной и легированной стали предел выносливости находится в точке пересечения левой и правой ветви выносливости (рис.6, а). При этом предполагалось, что переменные напряжения меньше ограниченного предела выносливости не оказывают влияние. Поэтому правая ветвь выносливости параллельна к оси абсцисс. Однако согласно ГОСТ 21354-87 на контактную выносливость оказывает влияние напряжение больше 0,75σ_Hlim, а на изгибную прочность - напряжения больше 0,6σ_Flim. Следовательно, правая ветвь не горизонтальна, а имеет некоторый наклон.

Вообще допущение о горизонтальности правой ветви выносливости противоречит физической сущности явления усталости, если рассматривать усталость как результат потерь на гистерезис при нагружении и разгрузке детали переменного режима работы. Оно также не согласуется с дислокационной теорией разрушения Тейлора, Оравана и Полани, которая подтверждает процесс постепенного искажения кристаллической решетки и структуры вследствие движения дислокаций и скопления вакансий под действием внутренних напряжений, в результате происходит образование очагов микротрещины даже в идеальных условиях.

Если учесть то обстоятельство, что фокусом трещинообразования по данным МГТУ им. Н.Э. Баумана могут быть микронеровности поверхности при R_Z>1 мкм или внутренние волосовины длиной l>20 мкм, то на длительную выносливость оказывает влияние напряжение меньше предела выносливости.

Из обобщенных диаграмм наиболее распространены диаграмма Смита (рис.6, б) где рассмотрены пределы выносливости при изгибе, растяжении-сжатии и кручении для коэффициента асимметрии -1≤R≤+1, характеристики цикла 0≤ρ≤∞, коэффициента амплитуды 0≤a≤1. Располагая диаграммами Смита для различных материалов и видов нагружения, можно производить расчет на усталость при любом значении коэффициента асимметрии цикла.

Для образцов и деталей при коэффициенте асимметрии R=-1 пределы выносливости для нормальных напряжении обозначают σ_-1 и (σ_-1)_D, а при кручении по симметричному циклу τ_-1 и (τ_-1)_D. Соответственно для отнулеванного цикла σ₀; (σ₀)_D и τ₀; (τ₀)_D.

При отсутствии табличных экспериментальных данных по ГОСТ 25.504-82 принимают следующие соотношения:

где - математическое ожидание предела прочности из 14 образцов по 14 плавкам. Так, для углеродистой стали:

Местные напряжения в деталях машинах

Опытным путем установлено, что на значение предела выносливости влияют размеры, форма и состояние поверхностей деталей.

Влияние размеров. Чем больше абсолютные размеры поперечного сечениях детали, тем меньше предел выносливости, так как в большей степени проявляются неоднородность механических свойств и внутренние структурные дефекты металла (раковины, шлаковые включения на границах зерен и др.). Это учитывают коэффициентом влияния абсолютных размеров поперечного сечения К_d (табл. 1, рис. 8).

Таблица 1. Значения коэффициента К_d (выборка)

Деформация и материал	Кd при диаметре вала d, мм
	20	30	40	50	70	100
Изгиб для углеродистых сталей	0,92	0,88	0,85	0,81	0,76	0,71
Изгиб для легированных сталей и кручение для всех сталей	0,83	0,77	0,73	0,70	0,67	0,62

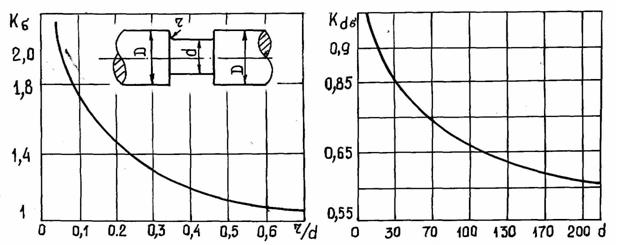
Рис.8

Влияние формы. В местах резкого изменения формы поперечного сечения или нарушения сплошности материала (в переходных сечениях, в резьбе, у канавок, выточек, отверстии и др.) напряжения больше номинальных σ или τ, определяемых по формулам сопротивления материалов.

Явление увеличения напряжений в местах изменения формы или нарушения целостности материала называют концентрацией напряжений.

Местные напряжения быстро убывают по мере удаления от концентратора, их вызвавшего (отверстия, канавки, паза и др.). Многократные изменения напряжений в зоне концентратора напряжений приводят к более раннему образованию трещины с последующим усталостным разрушением.

Влияние формы детали на предел выносливости учитывают эффективным коэффициентом концентрации напряжений K_σ(K_τ), равным отношению пределов выносливости при одинаковых видах нагружения двух образцов гладкого – σ_-1(τ_-1) и с концентратором напряжений - σ_-1K(τ_-1K):

Для наиболее характерных концентраторов напряжений значения K_σ и K_τ приведены в табл. 2.

Таблица 2. Значения коэффициентов K_σ и K_τ (выборка)

Концентратор напряжений	Kσ		Kτ
	σв стали, Н/мм
	≤ 700	> 700	≤ 700	> 700
Галтель (см. рис.7) при t/r = 2 и r/d = 0,02 при t/r = 2 и r/d = 0,05	1,85 1,8	2,0 2,1	1,55 1,6	1,65 1,7
Шпоночный паз, выполненный концевой фрезой	1,9	2,5	1,7	2,3
Шлицы: прямобочные эвольвентные	1,55 1,55	1,72 1,72	2,4 1,5	2,7 1,6
Резьба	2,1	2,7	1,6	2,2

Примечание. Если в расчетном сечении вала несколько концентраторов напряжений,

то в расчет принимают тот, для которого больше K_σ/K_d или K_τ/K_d.

Концентратором напряжений является и давление в месте установки деталей с натягом (зубчатых колес, подшипников качения). В этом случае влияния абсолютных размеров поперечного сечения вала на предел выносливости оказывается более резким. Для оценки концентрации напряжении учитывают отношения K_σ/K_d и K_τ/K_d (табл.3).

Влияния качества обработки поверхности. С увеличением шероховатости поверхности детали предел выносливости понижается.

При переменных напряжениях первичные усталостные микротрещины возникают обычно поверхностном слое. Этому способствует наличие следов инструмента (резца, шлифовального круга) после механической обработки, являющихся концентраторами напряжений. Влияние состояния поверхности на предел выносливости учитывают коэффициентом влияния качества обработки поверхности K_F (табл.4). Значительно снижает предел выносливости развитие коррозии в процессе работы.

Таблица 3. Значения K_σ/K_d и K_τ/K_d для валов в местах посадки деталей с натягом (выборка)

Диаметр вала d, мм	Kσ/Kd при σв, Н/мм^2				Kτ/Kd при σв, Н/мм^2
	700	800	900	1000	700	800	900	1000
30	3,0	3,25	3,5	3,75	2,2	2,35	2,5	2,65
50	3,65	3,96	4,3	4,6	2,6	2,78	3,07	3,26
≥100	3,95	4,25	4,6	4,9	2,8	2,95	3,2	3,34

Примечание. Наибольшая концентрация напряжений возникает у края напрессованной детали

Таблица 4. Значения коэффициента K_F (выборка)

Вид механической обработки	Параметр шероховатости Ra, мкм	Значения KF при σв, Н/мм^2
		≤ 700	> 700
Шлифование тонкое	до 0,2	1	1
Обтачивание тонкое	0,2…0,8	0,93	0,9
Шлифование чистовое	0,8…1,6	0,87	0,83
Обтачивание чистовое и фрезерование тонкое	0,8…3,2	0,8	0,75

Влияние упрочнения поверхности. Для повышения несущей способности деталей используют разные способы поверхностного упрочнения: цементацию, поверхностную закалку токами высокой частоты (ТВЧ), деформационное упрочнение (наклеп) накаткой роликами или дробеструйной обработкой. Упрочнение поверхности детали значительно повышает предел выносливости, что и учитывают коэффициентом влияния поверхностного упрочнения K_v (табл. 5).

Таблица 5. Значения коэффициента K_v (выборка)

Вид упрочнения поверхности вала	Значение Kv при Kσ
	≈1	> 1
Закалка ТВЧ	1,3…1,6	1,6…2,8
Азотирование	1,15…1,25	1,9…3,0
Накатка роликом	1,2…1,4	1,5…2,2
Дробеструйный наклеп	1,1…1,3	1,4…2,5

Коэффициенты снижения предела выносливости (K_σ)_D (K_τ)_D или комплексный фактор по ГОСТ 25.101-83 определяют с учетом приведенных выше коэффициентов:

где - коэффициент анизотропии.

Коэффициенты запаса прочности при статических напряжениях. Статические, или строго постоянные, нагрузки встречаются редко. К постоянным относятся нагрузки с отклонениями до 20% (действие сил тяжести, предварительной затяжки, давления газа или жидкости). Статистическим считается также такое нагружение, при котором число циклов за весь период работы N≤10³.

Для деталей из пластичных материалов при статическом нагружении концентрация напряжений не снижает несущие способности, так как местные пластические деформации способствуют перераспределению и выравниванию напряжений по сечению. В этом случае расчеты на прочность выполняются по номинальным напряжениям σ или τ.

Для малопластичных материалов (углеродистые и легированные стали) расчет ведут по наибольшим местным напряжениям, так как концентрация напряжений снижает прочность деталей.

Так же рассчитывают детали из хрупких материалов (высокоуглеродистых стали) в связи с их повышенной чувствительностью к концентрации напряжений. Однако детали из чугуна рассчитывают по номинальным напряжениям. Связано это с тем, что имеющиеся в структуре чугуна включения графита является очагами концентрации напряжений, приводящих к существенно большим местным напряжениям, чем те, которые обусловливаются конструктивными факторами (выточками, отверстиями).

На основания изложенного расчетные коэффициенты запаса прочности s, например, по нормальным напряжениям определяют по формулам:

для пластичных материалов

для малопластичных материалов

для хрупких материалов

для чугуна

где σ_T и σ_в - предел текучести и временное сопротивление материала; K_σ - эффективный коэффициент концентрации напряжений (см. табл. 2); [s]_T и [s]_В – допускаемые коэффициенты запаса прочности по пределу текучести и временному сопротивлению.

Выбор значения [s] является весьма ответственной задачей, поскольку необходима обеспечить требуемую надежность без завышения массы и габаритов детали. Ориентировочно рекомендуют:

для углеродистой стали [s]_T = 1,3…2,0;

для серого чугуна [s]_B = 2,1…2,4.

При переменных напряжениях. В этом случае для оценки сопротивления усталости деталей необходимо учитывать их конструктивные формы, размеры, состояние поверхности и другие факторы.

При действии переменных напряжении с амплитудой цикла σ_a, τ_a расчетные коэффициенты запаса прочности по пределам выносливости определяют по формулам:

в случае нормальных напряжений (изгиб, растяжение- сжатие)

в случае касательных напряжений (кручение, срез)

При совместном действии переменных нормальных и касательных напряжений, например при изгибе с кручением, общий коэффициент запаса прочности

где s_σ и s_τ - коэффициенты, определяемые по формулам (3), (4).

В случае переменных напряжений для стальных деталей рекомендуется принимать:

при высокой достоверности расчета [s]=1,3…1,5;

при менее точной расчетной схеме [s]=1,6…2,5.

Факторы, влияющие на сопротивление усталости деталей машин при действии переменных растягивающих нагрузок и крутящих моментов согласно ГОСТ 25.504-82 оказывает изменение на показатель кривой выносливости. Так, например показатель для левой ветви кривой выносливости валов определяется по следующей корреляционной формуле:

где K=(K_σ)_D - комплексный фактор;

- математическое ожидание предела прочности из 196 экспериментов.

По существующему стандарту ГОСТ 21354-87 для расчета зубчатых передач показатель кривой выносливости (рис. 6, а) по контактным напряжениям для левой ветви q_H=6, а для правой ветви - q_H1=20 и базовое число циклов N_Hlim=N_HG=N_HO=30HB^2,4≤1,2∙10⁸. Следует отметить, что по данным профессора Снесарева Г.А. показатель для правой ветви q_H1=24, а N_Hlim=HB^2,98≅HB³, чего подтверждает проф. Решетов Д.Н. Для шарикоподшипников q_H=9 и роликоподшипников q_H=10, а базовое число циклов по мнению Снесарева Г.А. N_Hlim=3∙10⁸.

Пределы выносливости для материалов зубчатых передач по ГОСТу 21354-87 имеют более стабильное значение, поэтому показателя для левой ветви при расчете на изгибную выносливость можно определить по следующей корреляционной формуле

где К=1,8…2 – для нормализованных и улучшенных колес;

К=2,6…2,8 – для закаленных и цементованных колес.

Для правой ветви показатель кривой выносливости Вёлера при изгибе

Здесь К=2,0…2,2 – для мягких зубчатых колес из-за образования дополнительной ступеньки;

К=2,8…3,0 – для твердых зубчатых колес;

σ_Fst - максимальное значение напряжения изгиба зубчатых колес при кратковременных перегрузках.

Следует отметить, что при q_F1≥50 можно считать правую ветвь горизонтальной и принимать Y_N=1.

Режимы работы и расчетные нагрузки машин

Достижения науки и техники уже на этапе проектирования зубчатых и червячных передач, валов, подшипников качения и других деталей позволяют учесть реальные режимы нагружения, что повышает надежность деталей и узлов общего назначения при одновременном уменьшении их габаритов и металлоемкости.

Нагрузки на детали машин могут быть постоянными и переменными по времени. Однако даже постоянные нагрузки во вращающихся деталях (валах, зубчатых и червячных колесах и т.д.) вызывают переменные напряжения. В деталях, у работающих машин, постоянные нагрузки встречаются редко, только в покое от собственного веса. Тем не менее, отдельные детали могут работать со слабо изменяющимися напряжениями, которые при расчете принимают условно за постоянные.

Нагрузки могут изменяться плавно или прикладываться мгновенно, так называемые динамические. Причины переменности нагрузок в машинах являются:

-неравномерность рабочего процесса двигателя;

-внутренняя динамика из-за неуравновешенности, а также погрешности изготовления детали и сборки узлов;

-неравномерность и переменность процесса рабочего органа машины (например, в строгальных, долбежных, протяжных станках, молотах и прессах, грузоподъемных машинах).

-переменность сил сопротивления и динамические воздействия при случайных перегрузках (универсальные металлорежущие токарные станки, резательные машины пищевых продуктов, специальные технологические машины, подверженные на выполнение различных операций с периодической настройкой). В общем случае переменными являются как амплитуды, так и средние значения нагрузок и напряжений.

Расчеты на выносливость, долговечность деталей машин за планируемый срок службы необходимо выполнять с учетом режима нагрузки. К режимам постоянной нагрузки условно относят режимы с отклонениями до 10%. При этом за расчетную обычно принимают нагрузку, соответствующую номинальной мощности двигателя. Это приводит к излишним запасам, к утяжелению конструкции. Этот худший случай нагрузки принимают за расчетный для неопределенных режимов нагрузки. Например, для редукторов общего назначения, которые используются в самых различных условиях. Переменность режима нагружения вызывается непостоянством полезных нагрузок и инерцией самой механической системы.

Двухпараметрическая или однопараметрическая схематизация позволяет свести повторно-непериодические напряжения к повторно- периодическим, изменяющимся по асимметричному знакопостоянному или знакопеременному симметричному циклу.

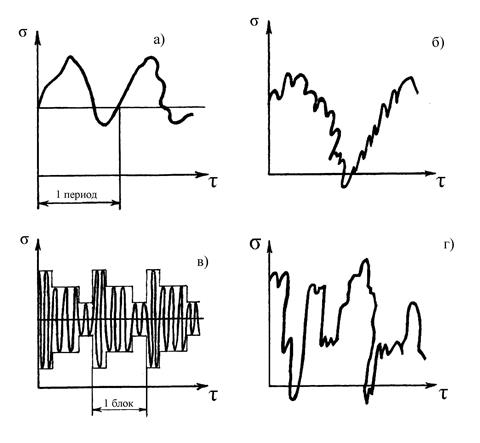
Рис. 9. Различный характер изменения напряжений во времени.

а - регулярное; б –бигармоническое; в – блочное; г – случайное напряжение

Рекомендуется 10 типовых и 36 эквивалентных режимов работы машин (рис. 10 и 11).

Вообще тяжелый режим I характерен для машин горнорудной и металлургической промышленности с круглосуточной работой; режим II-средний равновероятный характерен для технологического оборудования при 2-х сменной работе, режим III-средний нормальный присущ технологическому оборудованию и транспортным машинам. При полной односменной работе режим IV-легкий присущ универсальным машинам при односменной работе типа металлообрабатывающих станков и мясо-резательных установок; режим V-особо легкий присущ редко используемым машинам.

Большинство режимов работы современных машин можно свести к шести типовым режимам, представленным на графике рис. 10, в безразмерных координатах.

По оси абцисс отложено отношение числа циклов N_i с крутящим моментом Т_i суммарному числу циклов перемены нагружений N_Σ за весь период работы. По оси ординат отложено отношение крутящих моментов Т_і к максимальному длительному моменту Т_max. Длительно действующими называют крутящие моменты в спектре нагрузки, суммарное число циклов действия которых N>5∙10⁴ при расчете на изгибную выносливость и N>0,003N_HG при расчете на контактную выносливость, где N_HG=НВ^2,98- базовое число циклов при расчете на контактную выносливость.

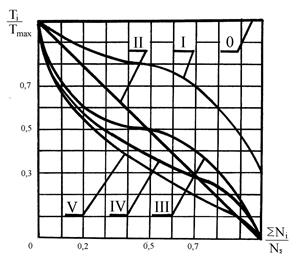
Рис. 10. Типовые режимы нагружения:

0 –постоянный; I –тяжелый; II-средний равновероятный;

III –средний нормальный; IV-легкий; V-особо легкий

Крутящие моменты Т_i или нагрузки F_i, у которых за всё время работы N<5∙10⁴ при расчете на изгибную выносливость и N<0,003N_HG при расчете на контактную выносливость, считают кратковременно действующими и при расчете деталей на выносливость не учитывают, поэтому упорядоченные графики нагрузки получаются ступенчатыми. Более глубоко изучены грузоподъемные машины, обобщенные графики нагрузки на основе эксперимента приведены на рис.11.

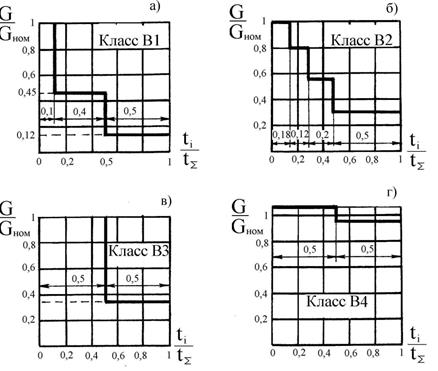
Рис.11. Типовые графики нагружения ГПМ

Следует отметить, если по ГОСТу 21357-87 по вертикальной оси типового режима отложена отношение длительно действующего наибольшего момента - T_i к максимальному моменту - T_max с учетом коэффициента внешней динамики - K_A по циклограмме нагрузок, то международный стандарт ISO6336 предусматривает принятия отношения длительно действующего наибольшего момента - T_i к номинальному моменту - T_ном с выделением K_A.

Для грузоподъёмных машин режим I называется весьма тяжелым (класс нагружения В4), что характерно подъёмным машинам горнорудной промышленности и металлургического производства с круглосуточной работой; режим II-тяжелый, присущ подъёмным машинам массового производства (класс нагружения В3), режим III-средний, присущ подъёмным машинам при односменной работе (класс нагружения В2), режим V-лёгкий (класс нагружения В1), присущ универсальным грузоподъёмным машинам, редко работающие с номинальным грузом. Такие режимы работы ГПМ соответствует ГОСТу 25546-82, который выполнен на основе международного стандарта ISO 4301-80.

Для машин непрерывного действия режим I -весьма тяжелый (класс использования В5); режим II -тяжелый (класс использования В4); режим III -средний (класс использования В3); режим ІV -легкий (класс использования В2); режим V -весьма легкий (класс использования В1).

Классы нагружения отражают относительную нагрузку механизма в соответствии со спектром нагрузок и зависят от значения коэффициента нагружения

где q- показатель кривой выносливости Вёлера;

α - показатель, характеризующий зависимость между нагрузкой и напряжением:

α =0,5 – при расчете на контактную выносливость зубчатых и червячных передач;

α =1/3 – при расчете на контактную прочность подшипников качения;

α =1 – при расчете на изгиб, растяжение- сжатие;

t_Σ - суммарное время работы за планируемый срок службы в часах;

F_i - нагрузка (сила, момент), действующая в течение времени t_i, за заданный срок службы;

F_max – наибольшая нагрузка, определяемая с учетом всех факторов согласно ГОСТ 25835 –83.

Следует заметить, что по ГОСТу 21354-87 коэффициент нагрузки называется коэффициентом эквивалентности по числу циклов нагружения и K_нагр=μ.

Для конвейеров при определении тягового усилия методом обхода по контуру рассматривается период установившегося движения тягового органа с грузом, поэтому называется тяговый расчет в статике и коэффициент внешней динамики здесь не учитывается.

Расчетная нагрузка при расчете на выносливость механических передач определяется по формуле:

T_p=K_A∙T₁∙K_E,

здесь К_А - коэффициент внешней динамики;

Т₁- номинальный максимально длительно действующий момент;

К_Е - коэффициент приведения режима с переменной нагрузкой к постоянному эквивалентному по усталостному воздействию.

Произведение (K_A∙T₁=T_max) коэффициента внешней динамики наибольшему длительно действующему моменту, на основании вышеуказанного положения, профессор Снесарев Г.А. называет максимальным моментом.

В зарубежной литературе эквивалентный момент по Винтеру Х. определяется по следующему выражению, так как К_А уже введен в расчетные формулы по определению контактной и изгибной выносливости:

T_E=K_E∙T₁

Расчетная нагрузка по Снесареву Г.Н. на выносливость имеет вид:

T_p=K_E∙T_max

здесь T_max=K_A∙T₁ и К_А в расчетные формулы не введены, а по зарубежным источникам данное выражение приобретает вид:

T_p=K_A∙T_E

Определение коэффициента внешней динамики К_А

При отсутствии данных непосредственных измерений или отраслевых рекомендаций по определению коэффициента внешней динамики – К_А рекомендуется использовать ориентировочные данные, приведенные в таблицах на основе стандарта ГОСТ 21354-87.

Таблица 6. Коэффициент внешней динамической нагрузки при расчетах на усталостную прочность – К_А

Режим нагружения двигателя	Режим нагружения ведомой машины
	равномерный	с малой неравномерностью	со средней неравномерностью	со значительной неравномерностью
Равномерный	1,00	1,25	1,50	1,75
С малой неравномерностью	1,10	1,35	1,60	1,85
Со средней неравномерностью	1,25	1,50	1,75	2 и выше
Со значительной неравномерностью	1,50	1,75	2,00	2,25 и выше

Коэффициент внешней динамической нагрузки, так называемый коэффициент внешней динамики, можно представить как произведение режима нагружения двигателя – К_ДВ и ведомой машины – К_Р,М, (таблицы 8 и 9).

К_А=К_двиг.∙К_р.м.

Данный коэффициент обычно задается предельными значениями К_{А min} и К_Аmax. Соответственно среднее значение

К_А=0,5(К_аmin+К_аmax)

Таблица 7. Характерные режимы нагружения двигателей

Режим нагружения	Вид двигателя
Равномерный КДВ=1,00	Электродвигатели общепромышленного назначения, паровые и газовые турбины при стабильных режимах эксплуатации и небольших пусковых моментах.
С малой неравномерностью КДВ=1,10	Крановые электродвигатели, гидравлические двигатели, паровые и газовые турбины при больших часто возникающих пусковых моментах.
Со средней неравномерностью КДВ=1,25	Многоцилиндровый двигатель внутреннего сгорания.
Со значительной неравномерностью КДВ=1,5	Одноцилиндровый двигатель внутреннего сгорания.

По предположению профессора Решетова Д.Н., все поля рассеивания покрываются шестью средними квадратическими отклонениями - S_А, получим

Соответственно коэффициент вариации будет

Характер режима нагружения ведомой машины зависит от условий эксплуатации, физико-механических свойств транспортируемого материала, характера нагружения рабочего органа, а также от погрешности изготовления отдельных деталей и сборки узлов. Поэтому коэффициент внешней динамики является случайной величиной (таблица 10).

Согласно ГОСТ 25835-83 режим работы механизмов ГПМ делится на четыре группы, и эквивалентная нагрузка определяется по формуле

F_E=K_Д∙F_max или T_E=K_Д∙F_max,

где К_Д - коэффициент долговечности

K_Д=K_G∙K_T∙K_ТР,

Таблица 8. Характерные режимы нагружения ведомых машин

Режим нагружения	Вид рабочей машины
Равномерный КР.М.=1,00	Электрический генератор; равномерно работающие конвейеры с тяговым органом; легкие подъемники, упаковочные машины; вентиляторы; мешалки для веществ равномерной плотности; турбокомпрессоры, легкие центрифуги; машины и механизмы с равномерно вращающимися деталями.
С малой неравномерностью КР.М.=1,25	Неравномерно работающие конвейеры с тяговым и без тягового органа; шестеренчатые и ротационные насосы; главные приводы станков; тяжелые подъемники, механизмы с вращающимися деталями кранов; промышленные и рудничные вентиляторы; тяжелые центрифуги и сепоратораторы большой производительности; перемешивающие устройства и мешалки для веществ с переменной плотностью; поршневые многоцилиндровые насосы и компрессоры; струйные и дозировочные насосы; экструдеры; каландры; вращающиеся печи; станы холодной прокатки.
Со средней неравномерностью КР.М.=1,50	Экструдеры для резины; мешалки с прерывающимися процессом; резательные машины пищевой промышленности; легкие шаровые мельницы; металло-и деревообрабатывающие станки и пилы, одноцилиндровые поршневые насосы; нереверсивные станы горячей прокатки, грузоподъемные машины тяжелой промышленности.
Со значительной неравномерностью КР.М.=1,75	Экскаваторы; черпалки; тяжелые шаровые мельницы, дробилки камня и руды; резиносмесители; кузнечные машины; тяжелые дозировочные насосы; ротационные буровые машины; брикетные прессы, реверсивные станы горячей прокатки.

здесь

- коэффициент, учитывающий переменность нагрузки во времени;

- коэффициент, учитывающий срок службы детали;

N_P - суммарное число циклов нагружения за расчетный срок службы;

N_FG=4× 10⁶ – базовое число циклов при расчете на изгиб, растяжения или на кручения;

N_HG = 10⁷ - базовое число циклов при расчете зубчатых колес по контактным напряжениям по данным ВНИИПТмаш (РТМ 24.090 - 76).

- коэффициент тренировки, при а=1;

K_TP=1 - при отсутствии кратковременных пиковых нагрузок;

a=1,35+0,5lgδ_ц - при наличии кратковременных перегрузок высокого значения

- коэффициент относительной продолжительности пиковой нагрузки, у которой число циклов нагружения равно - N_ц.

Таблица 9. Характерные режимы нагружения конвейерного транспорта

Условие эксплуатации	Характеристика транспортируемого груза	Характер нагружения	КР.О.-коэффициент нагружения рабочего органа	Вид средств механизации
Легкие	Формовочная земля, уголь дробленый, неабразивные сыпучие грузы: зерно, плоды и др.	Малая пульсация подаваемого материала с умеренной температурой окружающей среды	1,0…1,2	Ленточные и пластинчатые конвейеры с малой скоростью перемещения
Средние	Руды, горные породы, кусковые материалы до 150 мм, штучные грузы 30…100 кг.	Средняя пульсация подаваемого материала, небольшие толчки	1,2…1,4	Конвейеры скребковые, ленточные, цепные, пластинчатые, люлечные, тележечные и подъемники
Тяжелые	Руды, горные породы до 350 мм, штучные грузы массой до 500 кг.	Большая пульсация подаваемого материала, толчки средней силы	1,4…1,6	Эскалаторы, подъемники для бревен, пластинчатые, грузотолкающие конвейеры
Весьма тяжелые	Горные породы размером 500 мм, доломит, бревна диаметром до 900 мм, штучные тяжелые грузы до 1 т.	Толчки большой силы, опережающие удары, большая пульсация подаваемого материала	1,6…1,8	Ковшовые цепные элеваторы, цепные подъемники, грузотолкающие конвейеры

Момент при перегрузке по рекомендациям ВНИИПТмаш берется ниже следующих пределов:

Т_пик=К_пер ∙Т_ном ,

здесь К_пер-1,1- коэффициент перегрузки для механизма подъема;

Коэффициент перегрузки для механизма передвижения и поворота в зависимости от типа электродвигателя:

- крановый короткозамкнутый – 3,0

- крановый постоянного тока или переменного тока с контактным кольцом– 2,5

- асинхронный двигатель общепромышленного назначения – 1,75

Формула приводимая профессором Снесаревым Г.А. для определения эквивалентной нагрузки имеет вид

T_HE=K_НД∙T_max=K_G∙K_T∙T_max

здесь - коэффициент долговечности.

Как видим, предлагаемое выражение совпадает с методикой ВНИИПТмаш при коэффициенте тренировки равным единице. Механизмы грузоподъемных машин работают в повторно-кратковременном режиме, где продолжительность цикла не превышает 600 °С, поэтому расчеты стандарта ISO 6336-86 и ГОСТ 21354-87 существенно отличаются от предложенной методики Снесарева Г.А.

Кратковременные перегрузки, не учтенные при расчете на усталость деталей машин, могут привести к потере их статической прочности, поэтому необходимо проверить на статическую прочность при перегрузках.

Коэффициент внешней динамической нагрузки при перегрузках приведен в таблице 10. Пиковая нагрузка определяется по выражению

Т_пик=К_пер∙Т_ном=K_AS∙Т_ном

Выводы и рекомендации

Для расчета машин непрерывного действия при определении эквивалентной нагрузки на выносливость рекомендуется метод расчета Решетова Д.Н. и Винтера Х.

К определению коэффициента внешней динамики конкретной машины необходим дифференцированный подход с учетом конструктивной особенности и условий эксплуатации.

Точный график нагружения любой машины может быть определен только на основе длительного экспериментального исследования в условиях эксплуатации, но на этапе проектирования важен правильный выбор возможного графика нагружения.

Таблица 10. Коэффициент внешней динамической нагрузки при расчетах

на статическую прочность от максимальной нагрузки К_AS.

Вид рабочей машины и условия их эксплуатации	КAS	Примечание
Турбина-генератор при коротком замыкании	до 6	Перегрузка может быть уменьшена при помощи предохранительной муфты
Приводы с асинхронными электродвигателями при пуске	2,5 ... 5	Перегрузка может быть уменьшена путем рационального конструирования колебательной системы привода
Главные приводы металлорежущих станков с электродвигателями асинхронными или постоянного тока	1,8...4	Большие значения при неблагоприятных сочетаниях конструктивных и технологических параметров
Лебедки, строгальные и долбежные станки, скребковые конвейеры, фрикционные прессы	1,5...2,2	У ленточных и пластинчатых конвейеров перегрузки несколько меньше
Грузоподъемные машины: механизмы подъема, механизмы передвижения	1,2...2 1,5...4	Большие значения при подъеме груза с подхватом
Пилы для резки металла, ножницы, мясорезательные машины	1,8...2,5	--
Вентиляторы, воздуходувки	1,4...1,8	--
Трансмиссии машин	1,4...2,5	Меньшие значения у легковых автомобилей
Электрический транспорт	1,6...2,5	--
Вагоноопрокидыватели	1,8...5	--
Мельницы, глиномялки, смесители вязких масс	1,8...2,2	--
Камнедробилки	2,0...3,5	--
Кривошипные и эксцентриковые механизмы	1,8...3,0	--
Прокатные станы (удары при захвате)	2,5...4,5	--

Примечание: При наличии устройства для плавного пуска табличные значения следует уменьшить на 20 – 30%.

Вопросы для самопроверки

- Что следует понимать под циклом переменных напряжении? Характеристики цикла и соотношения между ними.

- Какой из циклов самый неблагоприятный для работы детали?

- Что называет усталостным разрушением и каковы его причины?

- Что называют пределом выносливости?

- Что такое концентрация напряжений и что ее вызывает?

- Как определяют общий расчетный коэффициент запаса прочности при переменных напряжениях?

- При каких обстоятельствах и где действуют контактные напряжения? По какой формуле определяют их наибольшее значение при начальном контакте по линии?

- В чем сущность усталостного выкрашивания хорошо смазываемых контактирующих под нагрузкой рабочих поверхностей? Как повысить сопротивляемость поверхностей выкрашиванию?

- Как определить число циклов за время работы детали?

- Стальные детали работают на изгиб по одинаковым циклам: одна на пределе выносливости, другая — при меньших напряжениях. Что можно сказать о долговечности этих деталей?

- Какие бывают концентраторы напряжений и как они влияют на выносливость детали?

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Строительная механика Теория машин и механизмов

00:00:00