Главная
Раздел 12. Вероятностные методы
расчета прочности и надежности механических систем
1. Вероятностный расчет на прочность
при статическом нагружении
1.1. Введение
Надежностью называется свойство объекта выполнять заданные функции, сохраняя во времени значения установленных эксплуатационных показателей в заданных пределах, соответствующих заданным режимам и условиям использования, технического обслуживания, ремонта, хранения и транспортирования. Количественно надежность определяется вероятностью безотказной работы. Вероятностью безотказной работы называется вероятность того, что при работе в заданных условиях система будет удовлетворительно функционировать в течение установленного промежутка времени. Таким образом, надежность имеет вероятностный характер.
Вероятность отказа как функция времени определяется следующим образом:
, 
, (1.1)
где t - случайная величина, обозначающая
наработку до отказа;
F(T) - вероятность того, что система выйдет из строя к
моменту времени T. F(T) представляет собой функцию распределения наработки до
отказа.
Вероятность безотказной работы или вероятность того, что невосстанавливаемая система
будет выполнять требуемую функцию в заданный момент времени t=T, можно записать в виде:
, (1.2)
где R(T) - вероятность безотказной работы.
Если случайная величина t имеет плотность распределения f(t), то
(1.3)
Так, например, если наработка до отказа имеет распределение Вейбулла
, (1.4)
то вероятность безотказной работы
равна:
, (1.5.)
где 
, 
, 
.
Среднее время безотказной работы 
определяется из
следующего выражения:
(1.6)
Частота, с которой происходят отказы
и неисправности, используется как параметр для математического определения
надежности. Этот параметр называется интенсивностью
отказов и измеряется обычно числом отказов за 1 час работы. Обратная
величина называется средней наработкой на отказ и измеряется в часах.
Вероятность безотказной работы в интервале 
; 
равна 
. Интенсивность отказов равна
(1.7)
Мгновенное значение интенсивности
отказов определяется как предел интенсивности отказов, когда длина интервала
стремится к нулю:
(1.8)
Для экспоненциального, Вейбулла и
нормального распределений плотность вероятности, вероятность безотказной работы
и интенсивность отказов имеют следующий вид:
экспоненциальное распределение:
,
(1.9)
распределение Вейбулла – Гнеденко:
;
; 
(1.10)
, (1.11)
где 
- параметры распределений.
Пример 1.1. Применительно
к нормальному закону распределения с параметрами 
циклов, 
циклов найти вероятность безотказной работы
элемента и интенсивность отказов при наработке 19000 циклов.
,
отказов/цикл.
1.2. Классификация отказов
Приработочные
отказы происходят в
течение раннего периода эксплуатации элемента конструкции. Они происходят
вследствие плохой технологии производства и плохого контроля качества.
Приработочные отказы могут быть исключены процессами отбраковки - приработки.
Для этого обычно элемент конструкции испытывают в условиях близких к эксплуатационным в течение некоторого времени. Износовые отказы возникают в конструкциях, которые
неправильно обслуживаются или совсем не обслуживаются. Причиной износовых
отказов является старение элементов конструкций. Износовые отказы в большинстве
случаев могут быть предотвращены за счет своевременной замены изношенных
элементов конструкций. Внезапные отказы не могут
быть устранены ни при отладке и при лучшем обслуживании. Они возникают
вследствие внезапной концентрации перегрузок, превышающих расчетную нагрузку.
Внезапные отказы иногда называют катастрофическими, что не совсем точно, так
как приработочные и износовые отказы также могут быть катастрофическими по
своим последствиям. Характеристики надежности элементов конструкций
определяются частотой внезапных отказов. Им уделяется главное внимание при
удалении причин, вызывающих приработочные и износовые отказы. На основании
вышеизложенного изменение интенсивности отказов с течением времени имеет вид
представленный на рис.1.1.
Рис.1.1. Изменение интенсивности отказов за срок службы
1.3. Определение вероятности безотказной работы
Чтобы оценить надежность, то есть
определить вероятность безотказной работы, необходимо знать распределения
действующих 
и предельных напряжений 
[1]. Обозначим через 
и 
– соответствующие плотности
распределения. Тогда вероятность безотказной работы ( см.
рис. 1.2.) имеет вид:
.
(1.12)
Вероятность
того, что предельное напряжение 
превышает
действующее напряжение 
равна:
. 
(1.13)
Вероятность
того, что действующее напряжение заключено в малом интервале 
, а предельное напряжение превышает напряжение, задаваемое
этим интервалом, при условии независимости случайных величин и 
, имеет вид:
. (1.14)
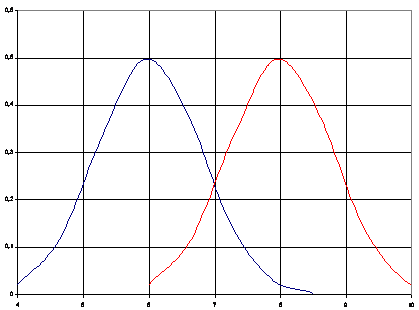
Рис.1.2. Плотности распределения
действующих и предельных напряжений
Рис. 1.3. К выводу формулы вероятности
безотказной работы
Это есть
площадь 
заштрихованного участка
на рис.1.3. Вероятность безотказной работы есть вероятность того, что
предельное напряжение превышает действующее напряжение для всех возможных значений действующих напряжений:
. (1.15)
или на основании свойств определенного интеграла:
.
(1.16)
В нижеприведенных примерах все расчеты выполнены в среде Mathcad.
Пример 1.2. Вывести
формулу для вероятности безотказной работы при нормальном
распределение действующих 
и предельных
напряжений.
Случайная
величина 
имеет нормальное
распределение с параметрами 
, где 
, 
. Вероятность безотказной работы равна:
. (1.17)
Если ввести
нормированную величину 
, то уравнение (1.17) будет иметь следующий вид:
, (1.18)
где
.
(1.19)
Уравнение (1.19) называется уравнением связи.
Принимая в
качестве коэффициента запаса статической прочности величину 
,
получим:
, (1.20)
где 
- коэффициенты вариации действующих и
предельных напряжений соответственно.
Пусть
известно, что напряжение, возникающее в элементе двигателя
имеет нормальное распределение с параметрами 
. Вследствие воздействия температуры предельное напряжение
имеет случайные колебания. Оно имеет нормальное распределение с параметрами 
. Определить вероятность безотказной работы.
По уравнению (1.19) имеем:
.
Пример 1.3. Вывести зависимость коэффициента запаса статической прочности от вероятности безотказной работы.
Решая уравнение (1.20) относительно величины n, получим следующее уравнение для расчета зависимости коэффициента запаса статической прочности от вероятности безотказной работы:
, (1.21)
где 
- квантиль нормированного нормального закона распределения
уровня R, то
есть соответствующая вероятности безотказной работы R.
В таблице 1.1. представлены результаты
расчета по формуле (1.21)
при 
.
Таблица 1.1
|
R |
0,5 |
0,99 |
0,995 |
0,99865 |
0,999 |
0,9999 |
0,99999 |
0,999999 |
0,9999999 |
|
|
0 |
2,32635 |
2,57583 |
2,99998 |
3,09023 |
3,71902 |
4,26489 |
4,74342 |
5,19934 |
|
|
1 |
1,31634 |
1,35502 |
1,42351 |
1,43855 |
1,54846 |
1,65203 |
1,75226 |
1,85098 |
Пример 1.4. Вывести формулу для вероятности безотказной работы при распределении Вейбулла-Гнеденко для действующих и предельных напряжений.
При
интегрировании по уравнениям (1.15),
(1.16) несимметричных
функций типа функции плотности распределения Вейбулла-Гнеденко: 
, 
. (1.22)
следует исходить из того, какое
из пороговых значений 
или 
больше. Если 
, то интегрировать следует по уравнению (1.15) с тем чтобы внешний
интеграл без учета внутреннего давал граничную величину равную единице. В этом
случае имеем:
. (1.23)
Так, например, при
,
вероятность безотказной работы по формуле (1.23) составляет 0,9616.
Если 
, то следует пользоваться формулой (1.16):
. (1.24)
Так, например, при
,
вероятность безотказной работы по формуле (1.24.) составляет 0,9766.
Пример 1.5. Вывести формулу для вероятности безотказной работы при нормальном распределении действующих и Вейбулла-Гнеденко для предельных напряжений.
, 
.
В этом
случае, чтобы получить однократный интеграл необходимо пользоваться формулой (1.15.), но поскольку
внутренний интеграл, при ограничении снизу нормального закона отличным от нуля
пороговым значением закона
Вейбулла-Гнеденко, не будет достигать единицы формулу (1.15) следует преобразовать следующим образом:
. (1.25)
Так,
например, при 
, вероятность безотказной работы по формуле (1.25) составляет
0,9645.
Аналогично производятся расчеты при Вейбулла-Гнеденко распределении для действующих и нормальном распределении для предельных напряжений.
, 
.
Пример 1.6. Определить допустимое значение внешней силы P при
растяжении полого стержня круглого
поперечного сечения (
=0,8) внешнего диаметра d=5 см, если математическое
ожидание предельного напряжения as=200 МПа, вероятность безотказной работы
равна R=0,999, коэффициент вариации предельного и действующего
напряжения соответственно равны: 
=0,07; 
=0,1.
Рис.1.4. Схема к примеру 1.6.
В соответствии с таблицей 1.1. коэффициент запаса
статической прочности при заданной вероятности безотказной работы 0,999 равен
1,4385. Наибольшее значение продольной силы действует на третьем участке и
равно 2P. Величина неизвестной внешней
силы определяется из следующего уравнения:
.
Пример 1.7. Проверить прочность полого вала (=0,8) внешнего диаметра d=3 см, если математическое
ожидание предельного напряжения as=350 МПа, вероятность безотказной работы
равна R=0,999, коэффициент вариации предельного и действующего
напряжения соответственно равны: =0,07; =0,1. Максимальный момент составляет 700 нм.
Фактическое значение коэффициента запаса статической
прочности при кручении определяется по следующей формуле:
Расчетный коэффициент запаса для заданной вероятности безотказной
работы 0,999 составляет 1,4385, то есть требуемый уровень надежности обеспечен.
Пример 1.8. Определить размеры прямоугольного поперечного сечения (
) балки при изгибе, если математическое ожидание
предельного напряжения as=200 МПа, вероятность безотказной работы равна R=0,999,
коэффициент вариации предельного и действующего напряжения соответственно
равны: =0,07; =0,1. Максимальный изгибающий момент составляет 1250 нм.
Действующие напряжения при изгибе определяются по следующей
формуле:
.
Размеры прямоугольного поперечного сечения определяются по следующей формуле:
.
Пример 1.9. Пусть стержень
круглого поперечного сечения диаметром d растягивается силой P. Предположим, что сила P является случайной величиной с
нормальным законом распределения с параметрами 
кН, 
Н. Временное
сопротивление S материала
стержня является также случайной величиной, подчиняющейся нормальному закону распределения
с параметрами 
МПа, 
МПа. Определить диаметр стержня при заданной
вероятности безотказной работы R=0,9999, если ожидаемое значение
коэффициента вариации диаметра
составляет 0,06.
Нормальные напряжения при
растяжении-сжатии определяются по формуле:
.
Дисперсия действующих напряжений по теореме о дисперсии функции случайных величин приближенно равна:
.
.
По уравнению связи (1.19) имеем:
.
Решая это
уравнение относительно 
методом
последовательных приближений получим 
м.
2. Вероятностный расчет на прочность
при переменных во времени напряжениях
2.1. Определение коэффициента запаса
прочности детали при регулярном асимметричном нагружении
Коэффициент
запаса усталостной прочности 
для базовой
долговечности, как правило
циклов, при регулярном нагружении в машиностроении обычно
определяется по известной формуле Серенсена-Кинасошвили [7]:
,
(2.1)
полученной на основании развития идей работы [9]. В формуле (2.1) приняты следующие обозначения:
- предел выносливости
гладкого лабораторного образца при симметричном цикле для базовой
долговечности;
, 
- характеристики
рабочего цикла изменения напряжений;
- коэффициент
чувствительности к асимметрии цикла;
- суммарный
коэффициент, учитывающий влияние концентрации напряжений, масштабного и
технологических факторов определяется из следующего уравнения [5]:
, (2.2)
где
коэффициент, учитывающий влияние концентрации напряжений и масштабного эффекта
определяется как отношение предела выносливости лабораторного образца к пределу выносливости
детали 
при симметричном цикле
изменения напряжений из следующего уравнения в соответствии с теорией подобия
усталостного разрушения [5]:
, (2.3)
- коэффициент
состояния поверхности, 
- коэффициент упрочнения, 
- коэффициент,
учитывающий состояния среды или коэффициент коррозионного воздействия, 
- теоретический
коэффициент концентрации для первого главного напряжения в зоне концентрации
рассчитываемой детали, 
- параметр наклона уравнения подобия, 
- параметр подобия для
детали.
Детальное исследование методов определения запасов прочности при асимметричном нагружении содержится в работе [10].
Формула (2.1) выведена в предположении линейной зависимости между предельной амплитудой и средним напряжением цикла как для образцов, так и для детали, приближенно схематизирующей действительную диаграмму предельных амплитуд, а также при пропорциональном возрастании амплитуды и среднего напряжения рабочего цикла вплоть до наступления предельного состояния. Вывод формулы (2.1) иллюстрируется рисунком 2.1.
Рис.2.1.
К выводу формулы коэффициента запаса
На рисунке
2.1 кривая линия представляет собой действительную диаграмму предельных
амплитуд. Верхняя прямая линия аппроксимирует кривую
диаграммы предельных амплитуд для лабораторных образцов, нижняя прямая – для
детали. Точка А (,) на рисунке 2.1 характеризует рабочий цикл
действующих на деталь напряжений, в то время как точка B (
,
) определяет предельную амплитуду для детали. Эти точки в
соответствии с принятым допущением лежат на одном луче. Коэффициент запаса
определяется из следующего уравнения:
.
(2.4)
В соответствии с принятой схематизацией диаграммы предельных амплитуд прямыми линиями, имеем:
, 
, 
. (2.5)
Подставляя соотношения (2.5) в (2.4), получим:
(2.6)
откуда после несложных преобразований получается формула (2.1).
Экспериментальные данные свидетельствуют о том, что форма диаграммы предельных амплитуд существенно отличается от прямой линии. В работе [11] на основании анализа известных уравнений диаграмм предельных амплитуд с привлечением большого числа опытных данных установлено, что наименьшей погрешностью обладает следующее корреляционное уравнение:
,
(2.7)
где 
- временное
сопротивление;
=0,63 - для алюминиевых сплавов;
=0,831 - для титановых сплавов;
=0,82 - для сталей.
Несколько большую погрешность имеет модель Хейвуда [12], полученная на основе детального анализа влияния средних напряжений цикла на предел выносливости сталей и алюминиевых сплавов при осевом нагружении:
, (2.8)
где F и 
- параметры (в МПа).
Для стальных гладких образцов:
. (2.9)
.
(2.10)
Для образцов из алюминиевых сплавов:
.
(2.11)
.
(2.12)
Следует
обратить внимание на ошибку в формуле для в
русском переводе работы [12].
Другие известные модели в ряде случаев не удовлетворяют граничным условиям, обладают большой погрешностью по отношению к имеющимся результатам экспериментов и поэтому в настоящей работе не рассматриваются.
Очевидно, что
коэффициент запаса усталостной прочности является функцией долговечности. При
этом все технологические и эксплуатационные факторы, входящие в формулу для (см. уравнение (2.2)) также, строго говоря, являются функциями
долговечности. Обоснование этих зависимостей производится, как правило, по данным
экспериментов. В работах [6,8,13], например, обоснованы следующие формулы для
учета зависимости наклона уравнения подобия усталостного
разрушения 
и коэффициента
чувствительности к асимметрии цикла 
от величины
долговечности 
применительно к легким
сплавам:
,
(2.13)
,
(2.14)
где 
- предел выносливости
при симметричном цикле нагружения для данной базы ;
- предел выносливости
при симметричном цикле нагружения для базовой долговечности 
циклов;
- справочные значения
характеристик для базовой долговечности циклов.
Для
установления зависимости предела выносливости от долговечности необходимо располагать
параметрами априорной кривой усталости материала при симметричном цикле
действия переменных напряжений.
Для
деформируемых алюминиевых сплавов применительно к гладким лабораторным образцам
диаметром 7,5-10 мм априорная кривая усталости может быть построена на
основании следующих уравнений в общем случае асимметричного нагружения с 
[14,15]:
(2.15)
для переменного изгиба;
(2.16)
для переменного растяжения-сжатия.
В формулах
(2.15),(2.16) представляет собой
ординату точек медианной кривой усталости, выраженную в мегапаскалях; - условный предел
прочности в той же размерности.
Для титановых сплавов, предел прочности которых находится в диапазоне 700-1300 МПа, априорные кривые усталости определяются по следующим уравнениям [16]:
, (2.17)
(2.18)
для переменного изгиба;
, (2.19)
(2.20)
для переменного растяжения-сжатия.
В работе [8] для большой группы алюминиевых и магниевых литых и деформируемых сплавов обосновано уравнение обобщенной кривой усталости, справедливое как для образцов, так и для элементов конструкций при симметричном нагружении:
(2.21)
Для уравнений диаграмм предельных амплитуд (2.7), (2.8) с учетом уравнений (2.13)-(2.21), устанавливающих зависимость параметров диаграммы от долговечности, можно уточнить формулу
(2.1) для коэффициента запаса. Рассмотрим эту методику на примере модели Степнова (2.7) с уточнением [11] на наличие концентрации напряжений (см. рис.2.2):
,
(2.22)
где
коэффициент 
определяется из следующих уравнений:
, (2.23)
а напряжение 
определяется из следующего уравнения:
. (2.24)
Предположим далее, что переход в предельное состояние происходит по степенной зависимости:
,
(2.25)
а коэффициент запаса усталостной прочности определяется как отношение предельной амплитуды детали к амплитуде рабочего цикла:
. (2.26)
В соответствии с уравнением (2.25) для предельной амплитуды имеем:
.
(2.27)
Выражая
параметр 
из уравнения (2.25) и подставляя (2.27) в
(2.26), получим:
. (2.28)
Аналогичная методика, примененная к уравнению Хейвуда, приводит к следующему уравнению для определения коэффициента запаса:
, (2.29)
где параметр 
определяется по
уравнениям (2.9), (2.11), а параметр с учетом уравнений
(2.10),(2.12) определяется из следующих уравнений:
- для сталей, (2.30)
- для алюминиевых
сплавов. (2.31)
Из уравнений
(2.28)-(2.31) численным методом нетрудно определить коэффициент запаса для заданных
напряжений рабочего цикла, характеристик механических свойств материала детали,
параметров диаграммы предельных амплитуд и коэффициента 
, определяющего интенсивность перехода в предельное состояние
в соответствии с уравнением (2.25). Соответствующие кривые предельных амплитуд
для образцов (кривая a),
детали без учета изменения коэффициента 
(кривая b) и для детали с учетом (кривая c), представлены на
рисунке 2.2. Там же показана кривая перехода в предельное состояние (кривая d).
На основании полученных уравнений формулы для расчета коэффициента запаса с учетом влияния долговечности будут иметь следующий вид:
, (2.32)
,
(2.33)
, (2.34)
(2.35)
для моделей Серенсена-Кинасовшвили (2.32), Степнова (2.33) и Хейвуда (2.34).
Рис.2.2. К выводу уточненной формулы
коэффициента запаса
Вид уравнений, определяющих зависимость конструкционных и эксплуатационных факторов усталостного разрушения от долговечности для деталей из алюминиевых, титановых сплавов и сталей в уравнениях (2.32)-(2.35) может уточняться по мере накопления экспериментальных данных и разработки теоретических моделей.
Пример 2.1. В
качестве примера рассмотрим расчет коэффициентов запаса для элемента
конструкции из алюминиевого сплава в диапазоне долговечностей 
циклов. Расчеты
выполнены для трех моделей (2.32), (2.33) и (2.34) при следующих значениях
характеристик: 
150 МПа; 
550 МПа; 
300 МПа; 
50 МПа; =0,3; =0,2; 
0,63; 
2, для двух значений теоретического коэффициента концентрации
напряжений детали 
=2,3 и 1,5. Параметр подобия принят равным - 
. Коэффициенты состояния поверхности, упрочнения, коррозии
примем равными единице. Расчетное значение напряжения для разных базовых
долговечностей в модели Степнова (2.33) определяется на основании уравнения
(2.24) с учетом уравнения кривой усталости (2.21):
. (2.36)
В таблицах
2.1, 2.2 представлены результаты расчета коэффициента запаса усталостной
прочности. Как видно из таблицы 2.1, рассчитанной для
значения теоретического коэффициента концентрации напряжений =2,3, модель Серенсена-Кинасошвили (2.32) дает большие
значения коэффициента запаса по сравнению с формулой (2.33), полученной на
основании модели Степнова с учетом изменения коэффициента , в среднем на 3-5% во всем диапазоне исследованных долговечностей
и амплитуд напряжений от 20 до 100 МПа. Исключение составляют лишь
значения при малой амплитуде 20 МПа и низких базовых долговечностей 
и 
циклов, для которых
коэффициент запаса по формуле (32) меньше на 1-3%. Если в формуле (2.33) не
учитывать значения , то есть принять =1, то коэффициент запаса в модели Степнова оказывается выше,
чем в формуле Серенсена-Кинасошвили. Причем это отличие достигает 10-18% при
малых амплитудах и долговечностях и снижается до 1-8% при возрастании рабочей
амплитуды и увеличении базовой долговечности до 
циклов. Формула
(2.34), полученная на основании модели Хейвуда дает большие значения
коэффициента запаса по сравнению с другими моделями во всем рассмотренном
диапазоне амплитуд и долговечностей. Это отличие по сравнению с формулой (2.32)
тем больше, чем меньше амплитуда и ниже базовая долговечность, и находится в
среднем в диапазоне 15-35%.
Таблица 2.1.
Результаты расчета коэффициента запаса усталостной прочности =2,3
|
|
|
|
||||||||
|
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
||
|
(2.32) |
|
2,354 |
1,703 |
1,334 |
1,096 |
0,931 |
0,808 |
0,715 |
0,640 |
0,580 |
|
|
2,053 |
1,469 |
1,144 |
0,937 |
0,793 |
0,687 |
0,607 |
0,543 |
0,491 |
|
|
|
1,846 |
1,311 |
1,017 |
0,830 |
0,702 |
0,607 |
0,536 |
0,479 |
0,433 |
|
|
|
1,737 |
1,229 |
0,951 |
0,776 |
0,655 |
0,567 |
0,499 |
0,446 |
0,403 |
|
|
(2.33) |
|
2,416 |
1,688 |
1,301 |
1,060 |
0,895 |
0,776 |
0,684 |
0,612 |
0,554 |
|
|
2,063 |
1,436 |
1,105 |
0,899 |
0,759 |
0,657 |
0,579 |
0,518 |
0,469 |
|
|
|
1,835 |
1,274 |
0,978 |
0,795 |
0,670 |
0,580 |
0,511 |
0,457 |
0,413 |
|
|
|
1,718 |
1,190 |
0,913 |
0,742 |
0,625 |
0,541 |
0,476 |
0,425 |
0,385 |
|
|
(2.33)
|
|
2,776 |
1,887 |
1,432 |
1,154 |
0,967 |
0,833 |
0,731 |
0,652 |
0,588 |
|
|
2,350 |
1,595 |
1,209 |
0,974 |
0,816 |
0,702 |
0,616 |
0,549 |
0,496 |
|
|
|
2,072 |
1,405 |
1,064 |
0,857 |
0,717 |
0,617 |
0,542 |
0,483 |
0,435 |
|
|
|
1,930 |
1,308 |
0,990 |
0,797 |
0,667 |
0,574 |
0,504 |
0,449 |
0,405 |
|
|
(2.34) |
|
3,171 |
2,166 |
1,647 |
1,331 |
1,117 |
0,962 |
0,846 |
0,754 |
0,681 |
|
|
2,645 |
1,804 |
1,371 |
1,106 |
0,928 |
0,800 |
0,702 |
0,626 |
0,565 |
|
|
|
2,313 |
1,577 |
1,198 |
0,967 |
0,811 |
0,699 |
0,614 |
0,548 |
0,494 |
|
|
|
2,168 |
1,478 |
1,123 |
0,907 |
0,761 |
0,655 |
0,576 |
0,513 |
0,463 |
|
Таблица 2.2.
Результаты расчета коэффициента запаса усталостной прочности 
=1,5
|
|
|
|
||||||||
|
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
||
|
(2.32) |
|
3,207 |
2,394 |
1,909 |
1,588 |
1,360 |
1,188 |
1,056 |
0,949 |
0,863 |
|
|
2,837 |
2,089 |
1,653 |
1,368 |
1,166 |
1,017 |
0,901 |
0,809 |
0,734 |
|
|
|
2,577 |
1,879 |
1,479 |
1,219 |
1,037 |
0,902 |
0,798 |
0,716 |
0,649 |
|
|
|
2,437 |
1,769 |
1,388 |
1,142 |
0,970 |
0,843 |
0,746 |
0,668 |
0,606 |
|
|
(2.33) |
|
3,877 |
2,684 |
2,058 |
1,671 |
1,408 |
1,217 |
1,072 |
0,958 |
0,867 |
|
|
3,311 |
2,283 |
1,748 |
1,417 |
1,193 |
1,030 |
0,907 |
0,810 |
0,733 |
|
|
|
2,936 |
2,020 |
1,544 |
1,251 |
1,052 |
0,908 |
0,800 |
0,714 |
0,645 |
|
|
|
2,743 |
1,886 |
1,440 |
1,166 |
0,981 |
0,846 |
0,745 |
0,665 |
0,601 |
|
|
(2.33)
|
|
4,150 |
2,834 |
2,156 |
1,742 |
1,462 |
1,260 |
1,108 |
0,988 |
0,892 |
|
|
3,521 |
2,401 |
1,824 |
1,472 |
1,235 |
1,064 |
0,934 |
0,834 |
0,752 |
|
|
|
3,109 |
2,116 |
1,607 |
1,296 |
1,087 |
0,936 |
0,822 |
0,733 |
0,661 |
|
|
|
2,899 |
1,971 |
1,496 |
1,206 |
1,011 |
0,871 |
0,765 |
0,682 |
0,615 |
|
|
(2.34) |
|
4,709 |
3,237 |
2,471 |
2,001 |
1,682 |
1,452 |
1,277 |
1,140 |
1,030 |
|
|
3,938 |
2,701 |
2,059 |
1,666 |
1,400 |
1,208 |
1,062 |
0,948 |
0,856 |
|
|
|
3,445 |
2,361 |
1,800 |
1,457 |
1,224 |
1,055 |
0,928 |
0,829 |
0,748 |
|
|
|
3,228 |
2,213 |
1,687 |
1,365 |
1,147 |
0,990 |
0,870 |
0,777 |
0,702 |
|
При снижении степени
концентрации напряжений в детали (см. таблицу 2.2, =1,5) и том же значении параметра подобия 
, рассмотренные сравнительные закономерности изменяются. Формула (2.33) дает большие значения коэффициента запаса по
сравнению с (2.32) практически во всем диапазоне амплитуд и долговечностей, но
это отличие достигает 13-20% при малых, 2-5% при средних амплитудах и
фактически равно нулю при возрастании амплитуды до 100 МПа. Как и в
таблице 2.1 формула (2.34) дает большие значения коэффициента запаса по
сравнению с (2.32) и (2.33). Как показали расчеты, изменение рабочего среднего
напряжения не влияет существенно на рассмотренные сравнительные закономерности.
Таким образом, на основании существующих уравнений диаграмм предельных амплитуд получены формулы для расчета коэффициента запаса усталостной прочности при регулярном нагружении, позволяющие производить расчеты коэффициента запаса в широком диапазоне рабочих амплитуд, средних напряжений и базовых значений долговечности до разрушения. Установлено, что наилучшее соответствие опытным данным имеет формула (2.33), полученная на основании уравнения диаграммы предельных амплитуд Степнова (2.22), хорошо апробированного для алюминиевых, титановых сплавов и конструкционных сталей.
Как
показывают расчеты для деталей из алюминиевых сплавов, формула
Серенсена-Кинасошвили (2.32) при значениях теоретического коэффициента
концентрации напряжений в детали 
>2 дает завышенный запас усталостной прочности по
сравнению с более точной формулой (2.33), полученной на основании модели
Степнова. При <2 несколько больший запас при малых рабочих амплитудах
дает формула (2.33), но при амплитудах, составляющих 50-70% от предела
выносливости на базе 
циклов отличие
коэффициентов запаса, рассчитанных по формулам (2.32) и (2.33) несущественно.
Во всех случаях формула (2.34), полученная на основании модели Хейвуда, дает существенно завышенный запас усталостной прочности по сравнению с другими моделями и ее применение для целей расчета коэффициента запаса не рекомендуется.
2.2. Расчет на прочность при регулярной переменной
нагруженности
Вероятностная трактовка условий прочности
деталей машин и элементов конструкций при регулярной переменной нагруженности
основывается на статистической оценке возможных случайных отклонений амплитуд
переменных напряжений и величины предела выносливости или его значений,
ограниченных по числу циклов, если рассматриваются условия прочности для
данного ресурса по числу циклов. Случайные отклонения амплитуды регулярной
переменной нагруженности деталей порождаются как случайными нарушениями режима
работы, связанными с воздействием регулирующих и управляющих данной машиной
систем, так и случайными отклонениями вследствие производственных и
эксплуатационных влияний. Вероятность безотказной работы определяется также как
и при статическом действии нагрузки. При этом в качестве предельного напряжения
берется предел выносливости детали 
, а в качестве
действующего напряжения - амплитуда действующего напряжения 
. Также как и ранее
считается, что эти величины статистически независимы. Предел выносливости
определяется по кривой усталости для заданной (базовой) долговечности. При
расчете следует учитывать, что характеристики рассеяния предела выносливости
существенно зависят от базовой долговечности. В качестве первого приближения
можно считать постоянным коэффициент вариации предела выносливости [1].
Пример 2.2.
Определить вероятность безотказной работы элемента конструкции при симметричном
цикле, соответствующую базовой долговечности циклов (вероятность
неразрушения до базовой долговечности) при действии амплитуды переменных
напряжений 
МПа. Коэффициент вариации действующих амплитуд
составляет 
. Предел выносливости при
симметричном цикле для указанной базы составляет 100 МПа. Коэффициент вариации предела
выносливости составляет 
. Примем нормальным закон
распределения предельных и действующих амплитуд переменных напряжений. По
уравнению связи имеем:
2.3. Расчет на прочность при
нерегулярной переменной нагруженности
Определение долговечности при
нерегулярном нагружении производится обычно по следующей схеме. На первом этапе
устанавливаются характеристики уровня нагруженности детали или элемента
конструкции в виде функции распределения амплитуд эксплуатационных напряжений.
В наиболее общем случае широкополосного процесса схематизацию случайного процесса
с целью построения функции распределения амплитуд напряжений, эквивалентных
случайному процессу по степени усталостного повреждения, производят одним из
известных методов: максимумов, экстремумов, размахов, полных циклов, «дождя» и
др. [4]. Метод полных циклов, например, дает, как принято считать, наряду с
методом «дождя» наиболее приемлемые результаты для оценки долговечности при
нерегулярном нагружении. Полученные величины амплитуд напряжений располагают в
возрастающем порядке, образуя вариационный ряд амплитуд. По величинам амплитуд
напряжений и соответствующим ординатам наносят точки на график и проводят через
эти точки линию. На основании анализа опытных данных, обработка осциллограмм
случайного процесса весьма часто приводит к эмпирическим функциям распределения
амплитуд напряжений существенно отличающихся от нормального или какого-либо
другого из известных законов распределения. Теоретический закон распределения
амплитуд напряжений зависит от метода схематизации эксплуатационных нагрузок и
во многих случаях оказывается трудно определимым. С целью практического
использования полученных эмпирических функций распределения при аналитическом
расчете ресурса предлагается [6] полиномиальная аппроксимация функции
распределения амплитуд напряжений, которую нетрудно
выполнить, например, в среде Mathcad.
2.4. Расчет долговечности при нерегулярном нагружении
Расчет на прочность при нерегулярной переменной нагруженности предполагает использование той или иной гипотезы накопления повреждений. Например, корректированная линейная гипотеза накопления усталостных повреждений [1] имеет следующий вид:
,
(2.37)
где 
-
количество циклов действия данной амплитуды переменных напряжений 
за срок службы 
;
-
долговечность до разрушения или до образования трещины заданного размера при
действии амплитуды (определяется по кривой усталости детали);
-
корректированная сумма повреждений
при действии всех повреждающих амплитуд переменных напряжений.
Значение определяется в зависимости от вида функции
распределения действующих напряжений по следующей формуле:
,
(2.38)
где 
-
элементарная вероятность попадания амплитуд в бесконечно малый диапазон;
.
(2.39)
-
функции распределения и плотности распределения действующих переменных амплитуд
соответственно.
В работе [1]
получена формула для определения величины , которая зависит от особенностей спектра эксплуатационной
переменной нагрузки:
,
(2.40)
где 
- максимальная
амплитуда действующих напряжений;
u – предел выносливости образца бесконечно большого диаметра или предельное повреждающее напряжение, принимаемое по данным [1] равным приблизительно половине предела неограниченной выносливости гладких лабораторных образцов стандартного размера:
,
(2.41)
.
(2.42)
Интегрирование в формуле (2.37) ведется по
всем амплитудам вплоть до максимальной амплитуды действующего спектра или блока
нагружения, превышающим предел неограниченной выносливости материала детали или
элемента конструкции 
. Интегрирование в формуле (2.42) ведется по амплитудам превышающим предельное повреждающее напряжение u. Схема расчета долговечности до разрушения иллюстрируется рисунком 2.3.
Окончательная формула для определения оценки среднего срока службы детали или долговечности до разрушения (образования трещины заданного размера) имеет на основании уравнений (2.37)-(2.42) следующий вид:
(2.43)
Таким образом, для определения оценки средней долговечности при нерегулярном переменном нагружении необходимо во-первых, знать функцию распределения действующих напряжений, которая оценивается по результатам анализа спектра эксплуатационной переменной нагрузки одним из известных методов схематизации (метод размаха, максимумов, полных циклов и т.п.), во-вторых, иметь кривую усталости детали при регулярном переменном нагружении для определения долговечности, стоящей в знаменателе формулы (2.43).
Рис. 2.3. Схема к расчету долговечности при
нерегулярном переменном нагружении
Этого
недостаточно для определения функции распределения долговечности при
нерегулярном нагружении, которая представляет особый интерес в связи с
необходимостью расчета гарантированного ресурса для ответственных деталей и
элементов конструкций авиационной техники. В работе [2] показано аналитически и
подтверждено экспериментально, что для оценки долговечности при нерегулярном
нагружении, соответствующей вероятности разрушения p, в формуле (2.43) вместо медианной
(p=0,5)
долговечности 
должна использоваться
долговечность 
(квантиль
долговечности), соответствующая вероятности p, которая определяется по кривой
усталости заданной вероятности разрушения (квантильной кривой усталости) (см.
рисунок 2.3.).
(2.44)
При варьировании величиной p получим функцию распределения долговечности до разрушения при нерегулярном переменном нагружении, общий вид которой представлен на рисунке 2.4.
Пример 2.3. Построить функцию распределения долговечности до разрушения детали из алюминиевого сплава при нерегулярном нагружении, заданном распределением амплитуд спектра эксплуатационной нагрузки в соответствии с законом Рэлея:
,
(2.45)
где параметр s=30 Мпа, максимальная
амплитуда 
Мпа. Эта функция
представлена на рисунке 2.5.
Пусть медианная кривая усталости детали при симметричном цикле имеет следующий вид:
,
(2.46)
где параметры
и 
равны соответственно
50 и 1000 МПа.
Рис. 2.4. График функции распределения
долговечности
до разрушения при нерегулярном переменном
нагружении
Рис. 2.5. Функция плотности
распределения амплитуд спектра эксплуатационной нагрузки.
Для расчета медианы долговечности достаточно этих данных. Для построения всей функции распределения необходимо располагать также параметрами квантильных кривых усталости, то есть кривых усталости, построенных по параметру вероятности разрушения. Так как построение семейства таких кривых требует большого числа экспериментальных данных, что не всегда возможно при длительных усталостных испытаниях, в первом приближении для вычисления квантили долговечности при регулярном нагружении воспользуемся известным приближением функции распределения логарифма долговечности на основании нормального закона:
, (2.47)
где 
определяется по
уравнению медианной кривой усталости (2.46), а среднее квадратическое
отклонение примем постоянным и равным 
=0,15, что в первом приближении подтверждается большим числом
экспериментальных данных [3] усталостных испытаний деталей, элементов
авиаконструкций и конструктивно подобных образцов из алюминиевых сплавов. В
формуле (2.47) 
- квантиль нормированного нормального закона распределения, соответствующая вероятности p. Тогда уравнение (2.44) для
определения функции распределения ресурса при нерегулярном нагружении примет
следующий вид:
, (2.48)
(2.49)
Расчет по формулам (2.48), (2.49), проведенный в среде Mathcad функции распределения долговечности при нерегулярном переменном нагружении представлен в таблице 2.3.
Таблица 2.3. Расчет функции распределения логарифма долговечности при нерегулярном нагружении
|
p |
0,01 |
0,05 |
0,1 |
0,2 |
0,3 |
0,5 |
0,7 |
0,8 |
0,9 |
0,95 |
0,99 |
|
(2.48) |
5,74 |
5,842 |
5,896 |
5,962 |
6,01 |
6,089 |
6,167 |
6,215 |
6,281 |
6,335 |
6,437 |
|
(2.51) |
6,45 |
6,552 |
6,607 |
6,673 |
6,72 |
6,799 |
6,878 |
6,925 |
6,991 |
7,046 |
7,148 |
В таблице 2.3 для примера представлен также расчет логарифма долговечности при той же нагруженности, но по степенному уравнению кривой усталости с нулевым значением предела неограниченной выносливости:
,
(2.50)
где параметр m=4, 
. На рисунке 2.6 построены графики этих функций на нормальной
вероятностной бумаге.
, (2.51)
(2.52)
p%
N
Рис. 2.6. Расчетные функции распределения
логарифма долговечности при нерегулярном нагружении по уравнениям (2.48)
(линия 1), (2.51) (линия 2).
Отметим, что
при расчете по уравнению (2.48) значение 
составило 0,283, а при расчете по уравнению (2.51)–0,373.
Кривые усталости для двух рассматриваемых в примере вариантов представлены на
рисунке 2.7.
Основой расчета долговечности при нерегулярной нагрузке, как видно из рассмотренных выше примеров, является обоснование уравнения кривой усталости детали при регулярном нагружении. Наиболее надежным способом обоснования такой кривой усталости являются прямые усталостные испытания натурных деталей с последующей статистической обработкой их результатов. Как показывают расчеты [6] для достижения достаточной точности оценивания характеристик усталостных свойств при усталостных испытаниях требуется порядка 30-50 объектов, что в условиях натурных испытаний является практически нереальным. В практике авиационных расчетных подразделений сложился комбинированный способ обоснования кривой усталости натурных деталей, суть которого заключается в выявлении опасных зон элемента конструкции (ресурсоограничивающих зон), изучении конструктивных и технологических особенностей этих зон, их нагруженности и последующего создания моделей или так называемых конструктивно-подобных образцов, которые по основным конструктивным, масштабным и другим характеристикам были бы подобны деталям в опасных зонах элемента конструкции. Испытаниям подвергаются в дальнейшем эти модельные образцы, стоимость которых ненамного выше обычных лабораторных образцов. В основном в качестве таких моделей в авиации используются для целей обоснования кривой усталости плоские образцы с отверстием, моделирующие масштабный эффект и концентрацию напряжений натурной детали. Полученная таким образом кривая усталости лишь приближенно отражает действительную кривую усталости элемента конструкции. Для уточнения такой кривой усталости по возможности следует проводить хотя бы единичные испытания натурной детали на одном уровне регулярной нагрузки. При этом в первом приближении можно считать, что показатель степени кривой усталости натурной детали равен показателю степени кривой усталости модельных образцов (то есть кривые усталости являются эквидистантными), но значение второго параметра уравнения кривой усталости, определяющего сдвиг одной кривой относительно другой, может быть уточнено.
В последние годы активно развиваются вероятностно-статистические методы обоснования расчетных характеристик выносливости натурных деталей, целью которых является построение кривых усталости натурных деталей и элементов конструкций без предварительных испытаний этих деталей, а лишь на основе некоторых критериев подобия усталостного разрушения, постоянство которых у моделей и натурной детали, обеспечивает возможность прогнозирования расчетных характеристик выносливости натурных деталей по результатам испытаний модельных образцов. Ниже рассматривается одна из таких теорий, получившая название статистической теории подобия усталостного разрушения профессора В.П. Когаева.
N
Рис. 2.7. Кривые усталости детали при
симметричном нагружении, построенные по уравнениям
(2.46) (кривая 1), (2.50) (кривая 2).
3. Обоснование кривой усталости натурных деталей и элементов
конструкций. Статистическая теория подобия усталостного разрушения
3.1. Вывод уравнения подобия усталостного разрушения
Для расчета деталей машин на усталость необходимо располагать характеристиками сопротивления усталостному разрушению натурных деталей. Наибольшую информацию об указанных характеристиках можно получить по полной вероятностной диаграмме, для построения которой требуется не менее 50-100 деталей, что во многих случаях осуществить невозможно. В связи с этим возникает необходимость разработки методов, позволяющих по результатам испытаний малых образцов и моделей средних размеров (конструктивно-подобных образцов) находить указанные величины для натурных деталей. Для этого необходимо обосновать критерий подобия усталостного разрушения, соблюдение постоянства которого у модели и детали обеспечивало бы совпадение функций распределения пределов выносливости.
Для решения этой задачи большую роль сыграли различные варианты статистических теорий прочности [1,2,3,4]. Статистическая теория прочности «наиболее слабого звена», предложенная Вейбуллом [4], позволила описать влияние абсолютных размеров образцов и неоднородности распределения напряжений на характеристики сопротивления хрупкому разрушению. Статистическая теория прочности Н.Н. Афанасьева [1] дала возможность охарактеризовать влияние конструктивных факторов на средние значения пределов выносливости деталей машин. Использование и развитие идей, содержащихся в указанных работах позволило В.П. Когаеву сформулировать [5] статистическую теорию подобия усталостного разрушения, которая дает удовлетворительное описание влияния конструктивных факторов на параметры функций распределения пределов выносливости. Эта теория послужила основой для создания новой системы справочной информации, предназначенной для определения расчетных статистических характеристик сопротивления усталости деталей машин.
Дальнейшее развитие теории подобия [6] позволило упростить расчеты и сократить число потребных параметров для ее функционирования, строить кривые усталости деталей машин и натурных элементов конструкций не только в случае деталей с неравномерным распределением напряжений в зоне концентрации, но и в случае крупногабаритных деталей без концентрации при переменном растяжении-сжатии.
Статистическая теория подобия усталостного разрушения дает описание влияния концентрации напряжений, масштабного фактора, формы поперечного сечения и вида нагружения на характеристики сопротивления усталости, определяемые по условию появления первой макроскопической трещины усталости. Характеристики прочности на стадии развития усталостной трещины и окончательного разрушения описываются методами механики разрушения. Под первой макроскопической трещиной усталости понимается трещина протяженностью до 0,1-0,5 мм, обнаруживаемая при усталостных испытаниях визуально, с помощью лупы или по началу снижения частоты собственных колебаний при испытаниях на резонансных усталостных машинах. Некоторая неопределенность в указании размера начальной трещины не имеет практического значения, так как у деталей с умеренной концентрацией напряжений пределы выносливости по началу образования трещины и по окончательному разрушению почти совпадают.
Рис.3.1.
Распределение первого главного напряжения в зоне концентрации
Выделим в окрестности
концентратора (рис. 3.1.) напряжений некоторый объем детали 
, достаточно малый для того, чтобы считать напряжения в нем
равномерно распределенными и равными 
, однако состоящий из некоторого количества ni, единичных объемов 
(
). Предположим независимыми события, заключающиеся как в
разрушении единичных объемов в пределах , так и в разрушении последних в пределах рассматриваемой
области. Тогда
вероятность разрушения i–го объема по теореме о вероятности одновременного наступления ni независимых событий будет иметь вид:
Рис. 3.2. Схемы к выводу формул
статистической теории подобия
усталостного разрушения
,
(3.1)
где 
- вероятность разрушения
единичного объема при действии напряжения 
. Примем, что эта вероятность распределена по закону
Вейбулла-Гнеденко:
при 
; (3.2)
при 
.
(3.3)
Подставляя выражение (3.2) в (3.1), получаем:
. (3.4)
Полагаем, что
разрушение любого из объемов , входящих в состав рассматриваемой области тела, означает
разрушение этой области, что эквивалентно рассмотрению всех , как образующих цепь последовательно соединенных n объемов
(звеньев). Тогда вероятность
разрушения рассматриваемой области тела по теореме о вероятности
одновременного наступления n независимых событий при действии максимального
напряжений 
, c учетом уравнения (3.4) равна:
,
(3.5)
где 
Суммирование
в (3.5) осуществляется только по тем объемам, в которых . Осуществляя предельный переход при
, получим:
,
(3.6)
где
(3.7)
или
.
(3.8)
Рассмотрим использование уравнения (3.8) для вывода основных уравнений теории подобия усталостного разрушения. Для этого целесообразно пренебречь влиянием второстепенных факторов, сделав некоторые допущения. Первое допущение, сделанное уже при выводе уравнения (3.8), заключается в пренебрежении влиянием второго и третьего главных напряжений. Второе допущение состоит в пренебрежении влияния длины и в замене интегрирования по объему интегрированием по площади поперечного сечения в уравнении (3.7). Второе допущение было сделано Афанасьевым и мотивировалось тем, что переход от одного сечения к другому не приводит к новой комбинации в распределении дефектов по сечению при волокнистой структуре с волокнами вдоль образца.
Под величиной
в уравнении (3.7)
понимается максимальное
напряжение в зоне концентрации, соответствующее пределу выносливости детали
, а именно:
, (3.9)
где - теоретический коэффициент
концентрации напряжений.
Для примера
рассмотрим брус прямоугольного поперечного сечения, изображенный на рисунке
3.1. Уравнение линии, заменяющей действительную эпюру
напряжений на участке 
, имеет вид:
,
(3.10)
где
.
(3.11)
Интеграл в уравнении (3.7) с учетом сделанных допущений получает вид:
. (3.12)
Выражая 
из уравнения (3.11) и
принимая
, после элементарных
преобразований получим:
. (3.13)
Выражение
(3.13) является функцией распределения предела выносливости детали. Множитель 
называется критерием
подобия усталостного разрушения, а уравнение (3.13) уравнением подобия, ибо если деталь и модель
имеют различные абсолютные и относительные размеры, но имеют одинаковые
значения параметра подобия, то функции их распределения совпадают. Эта
закономерность, справедливость которой подтверждается многими экспериментами,
имеет большое практическое значение, так как она дает возможность находить в
первом приближении функции распределения натурных деталей на основе испытаний
образцов и моделей. Легко установить, что все формулы и рассуждения остаются
без изменений, если нагружать брус знакопеременным изгибом, в случае круглого
бруса, пластин и в ряде других случаев. Параметр L представляет
собой часть периметра поперечного
сечения, в котором действуют максимальные напряжения, u –
трактуется как значение предела выносливости гладкого круглого бруса бесконечно
большого диаметра при изгибе с вращением и определяет нижнюю
возможную границу повреждающих напряжений, 
- относительный максимальный
градиент первого главного напряжения в зоне концентрации напряжений.
Незначительное
изменение формы функции распределения не имеет существенного значения, так как
надлежащий подбор параметров обеспечивает хорошее соответствие опытным данным.
Поэтому, если исключить величину 
, стоящую в знаменателе в формуле (3.13), после
логарифмирования, получим:
,
(3.14)
где 
.
Константа С определяется из условия, что для гладкого
круглого лабораторного образца стандартного диаметра 7,5 мм 
. При этих условиях и P=0,5,
и параметр 
. Окончательно, уравнение (3.14.) принимает следующий вид:
,
(3.15)
где
. (3.16)
В работе [5]
показано, что параметр u
приближенно равен 
- где 
представляет собой
предел выносливости гладкого лабораторного образца стандартного размера. В
таблице 3.1. представлены значения параметра 
по литературным
данным, приведенным в работе [5].
Таблица 3.1. Расчетные характеристики для некоторых материалов
|
Материал |
|
|
|
|
Сталь 45 |
660 |
307 |
0,1 |
|
Сталь 40Х |
2020 |
840 |
0,11 |
|
АВТ |
364 |
135 |
0,08 |
|
В95 |
618 |
174 |
0,09 |
|
АД33 |
333 |
127 |
0,09 |
|
Д16 |
554 |
166 |
0,20 |
|
ВМ65 |
267 |
113 |
0,10 |
|
Мл5 |
221 |
73 |
0,3 |
|
Модифицированный чугун |
830 |
350 |
0,15 |
|
30ХГСНА |
- |
730 |
0,10 |
, МпаЭкспериментальное
обоснование уравнения подобия в виде (3.15) получено в работе [6]. Там же установлено,
что параметр 
существенно зависит от
базовой долговечности и может быть приближенно определен в связи с вариацией
долговечности из следующего уравнения:
, (3.17)
где индексом N обозначены
характеристик для текущей долговечности, а индексом 107 соответствующие характеристики для
справочной базовой долговечности 107 циклов. Таким образом, для
построения кривой усталости натурной детали необходимо располагать параметрами
медианой кривой усталости гладких лабораторных образцов и справочным значением параметра
наклона уравнения подобия усталостного разрушения. Тогда функция
распределения предела выносливости натурной детали будет иметь следующий вид:
. (3.18)
Суммарный коэффициент, учитывающий влияние концентрации напряжений и масштабного фактора определится из следующего уравнения:
. (3.19)
Суммарный коэффициент, учитывающий влияние технологических факторов с учетом (3.19) равен:
,
(3.20)
где 
- коэффициент состояния поверхности, 
- коэффициент упрочнения, 
- коэффициент,
учитывающий состояния среды или коэффициент коррозионного воздействия.
Пример 3.1.
Определить вероятность
безотказной работы пластинки с отверстием из стали 40Х на базе 107 циклов при знакопеременном изгибе
Мпа.
Временное сопротивление 
=820
МПа. Коэффициенты вариации предела выносливости и действующей амплитуды равны
друг другу и не зависят от базы испытания: 
. Коэффициент чувствительности к асимметрии цикла составляет 
. Поверхности пластинки шлифованы, обработка поверхности -
развертка. Деталь работает при нормальной температуре без коррозионных воздействий.
Коэффициент состояния поверхности равен 
(рис.3.39 [5]). Коэффициент упрочнения равен единице. Кривая
усталости детали при симметричном цикле нагружения
имеет следующий вид:
,
(3.21)
где параметры
кривой усталости 
и B равны
соответственно 175 Мпа и 12000 Мпа. Параметр 
по таблице 3.1
принимаем равным 0,1. Предел выносливости на базе 107 циклов по уравнению (3.21) равен 420
Мпа.
Теоретический коэффициент концентрации
напряжений находим по рисунку 5.23 [5].
.
Параметр
подобия находим по формуле (3.58) [5]. 
. По формуле (3.19) определяем для базы 107 циклов
и вероятности Р=0,5
а с учетом влияния качества поверхности по формуле (3.20)
получим: 
. Коэффициент запаса усталостной прочности определяем по
формуле Серенсена-Киносошвили:
. (3.22)
Тогда вероятность безотказной работы определится на основании уравнения связи в предположении нормального закона распределения предельных и действующих напряжений по следующей формуле:
(3.23)
3.2. Вывод уравнения
подобия усталостного разрушения в случае однородного напряженного состояния
При переменном растяжении-сжатии и отсутствии у натурной детали концентрации напряжений формула (3.15) использоваться не может, так как в выражении для параметра подобия относительный максимальный градиент отсутствует. По этой причине в настоящей работе предлагается модифицировать уравнение подобия усталостного разрушения с целью использования критерия подобия в случае отсутствия градиента в распределении напряжений. При этом основное уравнение (3.7) остается без изменения. Подынтегральное выражение в уравнении (3.7) может быть вынесено из под знака интеграла в силу постоянства распределения напряжений по всему объему в рассматриваемой модели. Таким образом, задача сводится к физическому обоснованию величины интегрируемого объема в уравнении (3.7). Это может быть сделано из соображений, иллюстрируемых рисунком 3.3.
Рис. 3.3. К выводу формулы уравнения
подобия усталостного разрушения при однородном напряженном состоянии
Образование усталостных трещин начинается, как правило, на поверхности детали по следующим основным причинам: во-первых, на поверхности в большинстве случаев действуют наибольшие нормальные и касательные напряжения, во-вторых, зерна кристаллической структуры металла находятся в облегченных условиях деформирования, из-за того, что не стеснены соседними зернами, как это имеет место во внутренних слоях материала, в-третьих, на поверхности возникают естественные концентраторы напряжений из-за несовершенства обработки поверхности (риски, забоины, трещины и т.п.). По этой причине очевидным является предположение о необходимости интегрирования уравнения (3.7) лишь по некоторой малой части объема тела, вблизи поверхности, так как лишь эта часть объема определяет сопротивление усталостному разрушению детали. Очевидно, что размер этой зоны существенно зависит от целого ряда технологических, эксплуатационных и конструкционных факторов, количественное влияние которых учесть практически весьма затруднительно. Поэтому, не вдаваясь в детали, предположим, что глубина этой поверхности равна s, как это показано на рисунке 3.3.
Тогда, выполняя интегрирование в уравнении (3.7) по объему отмеченной зоны детали, получим:
,
(3.24)
где L – периметр сечения.
Пренебрегая
величиной 
по сравнению с
периметром, после элементарных преобразований получим:
,
(3.25)
где константа С определяется из соображений аналогичных тем, которые использовались при выводе уравнений (3.14)-(3.16). Таким образом, после логарифмирования, окончательно имеем уравнение подобия усталостного разрушения при равномерном распределении напряжений по сечению детали:
, (3.26)
где 
, коэффициент 1,3722 представляет собой логарифм периметра
гладкого лабораторного образца диаметром 7,5 мм, 
. Все остальные характеристики в формуле (3.26) аналогичны
тем, которые использовались в формулах (3.14)-(3.16). С учетом отличия
параметра наклона уравнения подобия (3.26) от параметра наклона уравнения
(3.16) (1/m и
1/(m+1)) и
необходимостью доступа к существующей справочной информации о величине , представляется целесообразным в первом приближении
определять величину 
из следующего
равенства:
. (3.27)
В таблице
3.2. представлены некоторые расчеты, выполненные по уравнению (3.26), для
разных значений , вероятностей разрушения и периметров деталей. Как видно из таблицы 3.2., для вероятности 50% наблюдается весьма
незначительное от 7 до 16% снижение предела выносливости детали по сравнению с
пределом выносливости стандартного лабораторного образца при значении 
, соответствующим большинству конструкционных сплавов (см.
таблицу 3.1.) с увеличением периметра детали от 100 до 1000 мм (значение L=1000 мм соответствует
диаметру круглого вала – 318 мм, в то время как значение 23,6 мм соответствует стандартному диаметру –7,5 мм). При
значении 
это снижении достигает
18 и 34% соответственно, что также следует признать несущественным с учетом
большого рассеяния характеристик усталостных свойств этой группы алюминиевых и
магниевых литых и деформируемых сплавов. Таким образом, расчеты в целом
подтверждают имеющиеся, правда, ограниченные, экспериментальные данные о весьма
незначительном масштабном эффекте для гладких деталей без концентрации
напряжений. Необходимо отметить, что детального экспериментального обоснования
этого вывода в настоящее время не существует. При снижении вероятности
разрушения до 1%, как видно из таблицы 3.2., максимальный расчетный диапазон
снижения предела выносливости достигает 17-45%.
В работе [7] приведены результаты усталостных испытаний образцов из сталей и легких сплавов диаметром до 40 мм. Результаты экспериментальных данных представлены точками на рисунке 3.4. На этом же рисунке построены по уравнению (3.26) кривые зависимости коэффициента масштабного фактора:
(3.28)
от диаметра
при переменном растяжении-сжатии образцов без концентрации напряжений для
вероятностей 0,1; 0,5 и 0,9 и 
.
Таблица 3.2. Значения 
в зависимости от
вероятности разрушения, периметра детали и наклона уравнения подобия (3.26)
|
P |
0,01 |
0,1 |
0,5 |
||||||
|
|
-1,839 |
-0,818 |
0 |
||||||
|
|
0,1 |
0,2 |
0,3 |
0,1 |
0,2 |
0,3 |
0,1 |
0,2 |
0,3 |
|
23,6 |
0,83 |
0,71 |
0,64 |
0,91 |
0,84 |
0,78 |
1,00 |
1,00 |
1,00 |
|
100 |
0,78 |
0,66 |
0,59 |
0,86 |
0,76 |
0,68 |
0,93 |
0,87 |
0,82 |
|
200 |
0,76 |
0,64 |
0,57 |
0,83 |
0,72 |
0,65 |
0,90 |
0,83 |
0,76 |
|
500 |
0,74 |
0,62 |
0,56 |
0,81 |
0,69 |
0,61 |
0,87 |
0,77 |
0,70 |
|
1000 |
0,73 |
0,60 |
0,55 |
0,79 |
0,66 |
0,59 |
0,84 |
0,74 |
0,66 |
Из рисунка 3.4 видно, что при растяжении-сжатии гладких образцов диаметром до 40 мм размеры существенного влияния не оказывают. При этом наблюдается существенный разброс величин масштабного коэффициента, полученных различными исследователями [1], что связано с малым числом испытанных образцов без учета рассеяния и с ярко выраженной зависимостью коэффициента масштабного фактора от типа материала. У неоднородных материалов, имеющих большое количество дефектов, влияние размеров выражено сильнее, чем у металлов однородных с меньшим количеством дефектов. Так, существенное снижение пределов выносливости с ростом размеров наблюдается у чугунов, для которых характерна большая неоднородность. При этом увеличение размеров поперечного сечения и массивности отливки приводит к резкому снижению характеристик прочности, определяемых на лабораторных образцах, изготовленных из отливок различного размера.
d, мм
Рис.3.4. Коэффициенты влияния абсолютных
размеров поперечного сечения при растяжении-сжатии для образцов из сталей и
легких сплавов без концентрации напряжений; сплошные линии – расчет по
уравнению (3.28) для различных вероятностей, ¨
- экспериментальные данные [7], *-
экспериментальные данные [8] сплавы АК4-1 и ВД17.
Литература
1. Афанасьев Н.Н. Статистическая теория усталостной прочности металлов. Киев, Изд. АН УССР, 1953, 123 с.
2. Болотин В.В. Статистические методы в строительной механике. М.: Стройиздат, 1965, 279 с.
3. Волков
С.Д. Статистическая теория прочности. М.: Машгиз, 1960,
176 с.
4. Weibull W.A. A
statistical theory of the strength of materials. Proc.
Royal Swedish Institute for Engineering Research.
5. Когаев В.П. Расчеты на прочность при напряжениях, переменных во времени. М.: Машиностроение, 1977, 232 с.
6. Агамиров Л.В. Разработка статистических методов оценивания характеристик усталостных свойств материалов и показателей надежности элементов конструкций авиационной техники. Докт. дисс. М.: МАТИ, 1994.
7. Серенсен С.В., Когаев В.П., Шнейдерович Р.М. Несущая способность и расчеты деталей машин на прочность. М.: Машиностроение, 1975, с.488.
8. Степнов
М.Н., Гиацинтов Е.В. Усталость легких конструкционных сплавов. М.: Машиностроение, 1976, с.230.
9. Soderberg C.R., Factor of Safety
and Working Stresses. Trans. Amer. Soc. Mech. Eng., vol. 52, part 1, 1930.
10. Киммельман Д.Н. Определение запасов прочности при переменных нагрузках асимметричных циклов, 1946.
11. Степнов М.Н. Расчетно-экспериментальный метод построения диаграмм предельных амплитуд для конструкционных деформируемых алюминиевых сплавов с учетом концентрации напряжений.// Вестник машиностроения.-1998.- № 9- с.11-17.
12. Хейвуд Р.Б. Проектирование с учетом усталости. М.: Машиностроение, 1969, с. 504.
13. Степнов М.Н., Мозалев В.В., Лисин А.Н., Агамиров Л.В., Евстратова С.П. Расчетный метод точечного и интервального оценивания квантильных кривых усталости деталей машин.// Проблемы машиностроения и надежности машин.-1994.- № 4.- с. 38 - 43.
14. Степнов М.Н., Евстратова С.П. и др. Расчетно-экспериментальные методы оценки характеристик сопротивления усталости конструкционных алюминиевых сплавов при асимметричном нагружении.// Проблемы машиностроения и надежности машин.-1998.- № 2.- с. 117 - 122.
15. Степнов М.Н., Николаев А.В. Расчетно-экспериментальные методы оценки характеристик сопротивления усталости конструкционных алюминиевых сплавов при осевом нагружении.//Заводская лаборатория.-1998.- № 7.- с. 38 – 40.
16. Степнов
М.Н. и др. Косвенная оценка пределов выносливости титановых сплавов при
переменном изгибе, растяжении-сжатии и кручении.//Заводская лаборатория.-1999.-
№ 3.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Строительная механика Теория машин и механизмов
