Главная
Раздел 5. Автоколебания
5.1.
Общие положения и примеры автоколебательных систем
Во всех рассмотренных ранее системах с неупругими сопротивлениями стационарные колебательные процессы оказывались возможными благодаря наличию внешних воздействий периодического характера. Однако в некоторых системах стационарные колебания возможны и без периодических воздействий извне; такие системы называются автоколебательными или самовозбуждающимися. Так как в любом реальном колебательном процессе неизбежно происходит рассеяние энергии, то всякая автоколебательная система обладает источником энергии, пополняющим все энергетические потери, но по своей природе источник не обладает колебательными свойствами.
Способность системы так регулировать отбор энергии от источника, чтобы появлялись автоколебания, определяется некоторыми ее свойствами. Этими свойствами являются динамические характеристики - собственные частоты и формы колебаний и коэффициенты затухания, определяющие «динамическую индивидуальность» системы.
Приведем несколько примеров возникновения
автоколебаний. Во многих случаях самовозбуждение колебаний возникает вследствие
взаимодействия системы с потоком жидкости, доставляющим энергию, необходимую
для поддержания колебаний системы. Так, если деревянный стержень полукруглого
сечения, подвешенный на пружинах, обдувать потоком воздуха, то стержень будет
совершать колебания в вертикальной плоскости, перпендикулярной к направлению потока,
причем с течением времени эти колебания становятся весьма интенсивными. Такой
стержень полукруглого сечения хорошо моделирует условия реальной проблемы - «галопирование» линий электропередачи. При некоторых
метеорологических условиях (главным образом при обледенении) провода линий
электропередачи, протянутые между пилонами, могут колебаться с весьма большими
амплитудами и низкими частотами.
Колебания стержня полукруглого сечения называют колебаниями системы с одной степенью свободы. Это означает, что движение совершается по одной форме, и соответствующее перемещение системы «стержень - пружины» можно охарактеризовать одной переменной величиной, например вертикальным отклонением центра тяжести стержня от своего среднего положения. Возможен такой тип автоколебаний, которые могут существовать лишь в случае возбуждения более чем одной степени свободы. В этом случае все положения, которые принимает система в процессе колебаний, могут быть описаны лишь при помощи более чем одной переменной величины.
Примером такой системы являются автоколебания крыла самолета в воздушном потоке. Длинная гибкая опора позволяет крылу перемещаться вверх и вниз как жесткому целому (таким же образом движется и стержень полукруглого сечения); это движение соответствует первой степени свободы. Движение, соответствующее второй степени свободы, - это поворот крыла вокруг своей оси, сопровождающийся деформацией тонкой листовой пружинки; при таких колебаниях изменяется наклон крыла относительно набегающего потока. Система имеет и другие степени свободы (так, крыло может перемещаться параллельно потоку), но они не играют существенной роли. При достаточно высокой скорости потока крыло совершает вертикальные колебания, и одновременно происходят изменения угла наклона крыла относительно набегающего потока (угла атаки). Это пример классического флаттера-движения, происходящего с двумя степенями свободы.
Флаттер может возникать также у лопастей вертолетов и лопаток турбомашин. На практике явление флаттера служит объектом обширных исследований; условие отсутствия флаттера часто является одним из основных требований при проектировании.
Возникновение флаттера связано с выбором «формы флаттера», для которой выполняются определенные соотношения между амплитудами и фазами колебаний, соответствующих различным степеням свободы. Условие возникновения флаттера зависит от скорости потока, а также от плотности и температуры воздуха. Предположим, что скорость изменяется. От скорости потока зависит значение энергии, получаемой системой за один цикл колебаний, и значение энергии, рассеиваемой за цикл колебаний вследствие внутреннего и аэродинамического демпфирования. Когда отношение этих значений энергии становится равным единице, в системе могут установиться колебания постоянной амплитуды; соответствующая скорость самолета называется критической скоростью флаттера. Каждой из возможных форм флаттера соответствует своя критическая скорость, и все расчеты флаттера проводятся с целью удостовериться, что наименьшая из критических скоростей с достаточным запасом превышает максимально возможную скорость полета самолета.
Существуют три пути борьбы с флаттером.
Первый способ основан на таком изменении характеристик системы, при котором достигается независимость колебаний, соответствующих различным степеням свободы, причем демпфирование всех этих различных форм колебаний положительно. Так, можно добиться того, чтобы поворот оси профиля крыла относительно продольной оси сечения слабо зависел от вертикального перемещения оси. Для этого нужно, чтобы ось занимала определенное положение, а распределение массы по сечению профиля удовлетворяло определенному условию. Другой способ заключается в увеличении собственных частот конструкции за счет увеличения отношений «жесткость/масса» отдельных ее частей. Этот способ основан на том, что энергия, получаемая системой при флаттере за один цикл колебаний, почти не зависит от частоты, тогда как энергия, рассеиваемая за один цикл, пропорциональна частоте.
Два рассмотренных метода обычно используются в практике самолетостроения. Третий метод борьбы с флаттером, вызываемым аэродинамическими силами, не всегда эффективен, но часто с успехом используется для устранения других видов автоколебаний. Этот метод заключается в демпфировании системы. Увеличивая трение в системе, склонной к флаттеру (т.е. увеличивая энергию, рассеиваемую за один цикл колебаний заданной амплитуды) можно, как правило, повысить критическую скорость системы.
5.2.
Фрикционные автоколебания
Особого внимания заслуживают механические автоколебания, возникающие в системах с трением. Сила трения, которая в ранее рассмотренных примерах оказывалась причиной затухания колебаний, может явиться причиной их раскачивания.
Рассмотрим простейшую систему (рис.62,а), состоящую из двух вращающихся барабанов и бесконечной ленты.
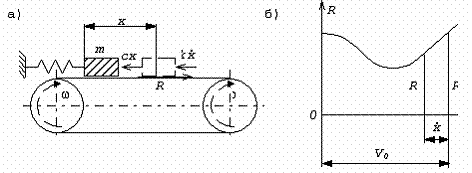
Рис. 62
На ленте
лежит груз массой 
, движение которого ограничено пружиной с жесткостью с. Развивающаяся при скольжении груза сила трения смещает груз
вправо и вызывает некоторое удлинение пружины. Пусть в положении равновесия
груза сила трения равна R0,
тогда статическое смещение груза
(161)
Для дальнейших рассуждений необходимо учесть, что сила трения R зависит от относительной скорости движения V (при заданном нормальном давлении груза, которое будем считать постоянным). Пусть характеристика трения имеет вид, показанный на рис.62,б, где значения V0 и R0 соответствуют состоянию равновесия груза.
Положим, что
вследствие какого-либо возмущения в мгновение t=0 груз выведен из состояния покоя.
Выясним характер движения, которое возникает после такого возмущения, считая,
что скорость движения ленты в процессе колебаний груза не изменяется. Пусть в
текущее мгновение 
смещение груза равно 
, его скорость равна 
, а скорость скольжения
.
В это
мгновение на груз действуют три силы: сила трения R, реакция пружины 
и внешнее
сопротивление, которое будем считать пропорциональным скорости и равным 
.
Сила 
отличается от силы 
, поскольку скорость относительного движения 
отличается от скорости
. При малых колебаниях относительной скорости можно принять:
,
(162)
где 
- тангенс угла наклона
характеристики трения в точке с координатами 
.
Уравнение движения груза:
.
Подставляя сюда (162), получим
или
(163)
Сместим
начало отсчета перемещений в точку 
, т.е. введем новую переменную 
.
Тогда (163) имеет вид
Согласно (161), сумма двух последних слагаемых равна нулю, поэтому получим уравнение
(164)
Анализ
структуры этого уравнения показывает, что с увеличением времени колебания
должны исчезать, если сумма 
положительна. Это
обязательно имеет место на восходящем участке характеристики трения, где 
.
Однако при
небольших значениях (нисходящий участок
характеристики трения) величина становятся
отрицательной. Если при этом 
, то сумма остается
положительной, и колебания будут затухающими. Если сумма обращается в нуль,
т.е. 
, то в уравнении (164) исчезает член, соответствующий
затуханию, и становятся возможными колебания с постоянной амплитудой. Если же
сумма отрицательна, то
система обладает как бы «отрицательным затуханием», и колебания с течением
времени будут возрастать за счет энергии, передаваемой движущейся лентой.
Природу «отрицательного затухания» при падающей характеристике трения можно выяснить исходя из следующих рассуждений. Когда груз движется вправо, т.е. по ходу движения ленты, относительная скорость скольжения уменьшается; вместе с этим сила трения увеличивается и ее приращение направлено вправо, т.е. также в сторону движения. В другом интервале движения, когда груз движется влево, приращение силы трения направлено также влево, т.е. опять в сторону движения. Такой характер изменения силы трения и является причиной возрастания колебаний.
Итак, для
возрастания колебаний необходимо выполнение условия: 
, что возможно только при достаточной крутизне падения
характеристики трения. Обычно указанное условие выполняется лишь при малой
скорости .
При помощи тех же рассуждений можно прийти к выводу о возможности автоколебаний упруго закрепленной колодки, прижатой к вращающемуся диску (рис.63,а), а также груза на пружине, когда левому ее концу задано движение с постоянной скоростью (рис.63,б). В обоих этих случаях необходимым условием автоколебаний также является наличие нисходящего участка характеристики трения.
К этому же
классу явлений относятся автоколебания, возникающие при резании металлов на
станках. Рассмотрим природу этих автоколебаний. Со стороны заготовки на резец
действует реакция 
, которая может быть разложена на составляющие 
и 
(рис.63,в,г). Резец упруго закреплен и его конец может совершать колебания как в горизонтальном, так и в вертикальном
направлениях. Для выявления возможности автоколебаний достаточно рассмотреть
колебания только в горизонтальном направлении 
и учесть важный
экспериментальный результат: горизонтальная составляющая зависит от скорости
горизонтальных колебаний резца 
.
На резец
действуют три силы: сила упругости - су
системы резец-суппорт (где с -
коэффициент жесткости); реакция заготовки 
и сумма различных
неупругих сопротивлений, которая может быть объединена в одно слагаемое вида 
.
Рис. 63
Таким образом, уравнение движения системы резец-суппорт имеет вид
где - приведенная масса
системы резец-суппорт.
После
линеаризации силы , согласно (162), вновь приходим к уравнению типа (164),
следовательно, и в этом случае автоколебания возможны, если характеристика силы
- нисходящая.
Как
установлено, неустойчивость состояния равновесия может быть обнаружена в
предположении малости колебаний, т.е. при помощи линейного приближения. Однако, если отказаться от этого предположения и проследить за дальнейшим течением процесса,
то обнаруживается, что рост амплитуд постепенно замедляется и в конечном итоге
амплитуда полностью стабилизируется. Этот процесс установившихся (стационарных)
автоколебаний (рис.64) называется предельным
циклом.
Важной особенностью предельного цикла является
его полная независимость от начальных условий; после любого возмущения
состояния равновесия система приближается к одному и тому же предельному циклу.
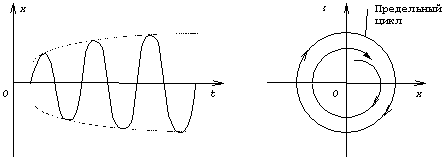
Рис. 64
Для выявления параметров (частоты, амплитуды) установившихся автоколебаний необходим анализ соответствующей нелинейной задачи.
В некоторых случаях
стационарные автоколебания носят почти гармонический характер и совершаются с
частотой свободных колебаний системы; соответствующие системы называются квазилинейными. В
других случаях стационарные автоколебания резко отличаются от гармонических, сопровождаются
остановками и скачками скорости; такие автоколебания и соответствующие системы
называются релаксационными или разрывными.
5.3.
Флаттер крыла в воздушном потоке
Как уже говорилось выше, флаттером называются автоколебания тел в потоке газа или жидкости.
При появлении первых скоростных самолетов флаттер служил причиной многочисленных катастроф. Явление флаттера тесно связано с теми воздействиями, которые поток воздуха оказывает на колеблющееся крыло.
Ограничимся рассмотрением принципиальной картины этого явления. При флаттере крыло самолета совершает изгибно-крутильные колебания, поэтому для анализа этого явления необходимо учесть по крайней мере две степени свободы крыла. При практических расчетах достаточно учесть движения крыла по первым формам собственных изгибных и крутильных колебаний. В еще более простом варианте расчета рассмотрим жесткое крыло, имеющее две степени свободы, соответствующие его вертикальному перемещению и повороту (рис.65).
Существенное значение имеет положение центра тяжести крыла, т.е. той точки его хорды, приложение вертикальной силы в которой вызывает только вертикальное перемещение крыла, но не его поворот. К этой точке (точка 0 на рис.65) будем приводить действующие на крыло силы.
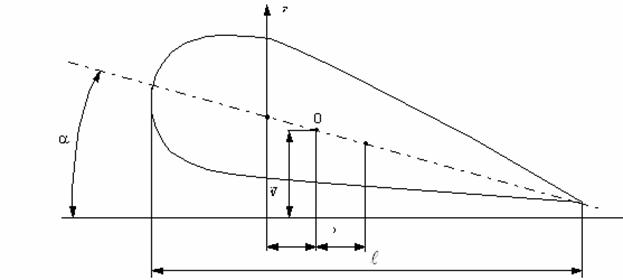
Рис. 65
Если
обозначить вертикальное перемещение центра жесткости крыла через 
, а изменение угла атаки крыла в процессе движения через 
, то упругие сила и момент, приложенные в точке 0, будут
равны соответственно 
и 
, где 
и 
- коэффициенты
жесткости.
Сила инерции и момент сил инерции относительно точки 0 составляют соответственно
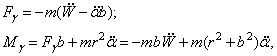(165)
где 
- расстояние от центра
жесткости крыла до его центра массы; - масса крыла; 
- радиус инерции массы
крыла относительно центральной оси.
Наибольшие трудности представляет определение
изменений аэродинамических сил, возникающих вследствие движения крыла.
Простейшая гипотеза относительно этих сил состоит в том, что их можно вычислить
так же, как и при неподвижном крыле, подставив в соответствующие формулы
значения мгновенного угла атаки. В этом предположении получаем увеличение
подъемной силы и момента
(166)
где 
- плотность воздуха; - скорость потока; 
- площадь сечения
крыла; 
- расстояние от центра
тяжести до центра давления, который расположен на одной четверти хорды крыла.
Формулы (166)
представляют собой грубое приближение, так как в них полностью игнорируется
влияние движения крыла на обтекание. Более точное решение задачи показывает,
что если крыло совершает, например, гармонические колебания с частотой 
, то следует учитывать еще инерцию присоединенной массы
воздуха и то обстоятельство, что изменение подъемной силы оказывается смещенным
по фазе относительно изменения угла атаки.
Как величина
присоединенной массы, так и фазовый сдвиг зависят от безразмерного параметра 
, характеризующего частоту колебаний.
Ради
упрощения расчета не будем учитывать всех этих обстоятельств и дополнительно в
первой из формул (166) пренебрежем слагаемым 
, которое характеризует аэродинамическое демпфирование
вертикальных колебаний крыла. С учетом сказанного получаем уравнения движения
крыла в виде
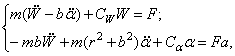(167)
где 
.
Решение системы (167) отыщем в виде, соответствующем
гармоническим колебаниям:
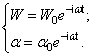(168)
Подставляя
(168) в (167), получим систему однородных алгебраических уравнений относительно
и 
:
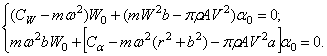(169)
Приравнивая нулю определитель системы (169), получим частотное уравнение. Для того чтобы привести это уравнение к более простому виду, введем следующие обозначения:
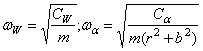
- собственные частоты поступательных
(изгибных) и крутильных колебаний крыла;
-
относительная плотность крыла.
Тогда частотное уравнение можно представить в так:
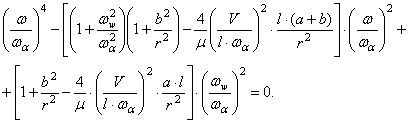(170)
При нулевой скорости потока V=0 это уравнение даёт два положительных значения W2, соответствующих двум собственным частотам системы.
С увеличением скорости потока возможно появление двух типов неустойчивости. Так, один из корней уравнения (170) может обратиться в нуль, что соответствует обращению в нуль свободного члена уравнения (170):
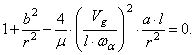(171)
Обращение в нуль частоты собственных колебаний системы свидетельствует о её статической неустойчивости. Действительно, возвращаясь в формуле (171) к первоначальным обозначениям, приведём её к виду
Если это соотношение выполняется, то при повороте крыла на угол а момент дополнительной подъёмной силы
уравновешивается упругим моментом .
Явление статической потери устойчивости крыла при достижении скоростью потока значения Vg называется дивергенцией.
Для крыльев самолётов, как правило, скорость дивергенции существенно превышает скорость полета и дивергенция не представляет реальной опасности.
Другой вид
потери устойчивости – изгибно-крутильный флаттер - связан с тем, что частоты,
определяемые из (170), становятся
комплексными числами. Если имеются сопряжённые комплексные частоты 
, то соответствующие решения уравнений движения имеют
множители
.
Экспоненциальные множители с действительными положительными показателями неограниченно возрастают.
Таким
образом, в этом случае движение представляет собой колебания с нарастающими амплитудами (колебательный характер движения определяется
множителями 
).
Итак, условием наступления флаттера является появление комплексных корней уравнения (170), что происходит при обращении в нуль (назовём это «граничным условием») его дискриминанта:
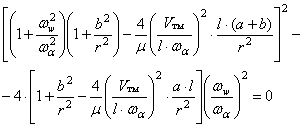(172)
Из уравнения (172) легко вычислить скорость флаттера.
Проследим на числовом примере характер изменения частоты свободных колебаний крыла по уравнению (170) при увеличении скорости потока.
Допустим, что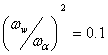 
; 
; 
; 
; 
.
Этим данным соответствуют
скорость дивергенции, вычисленная по уравнению (171), 
, и скорость флаттера, вычисленная по уравнению (172),
.
График изменения частот колебаний системы в зависимости от скорости потока, построенный в соответствии с уравнением (170),показан на рис.66.
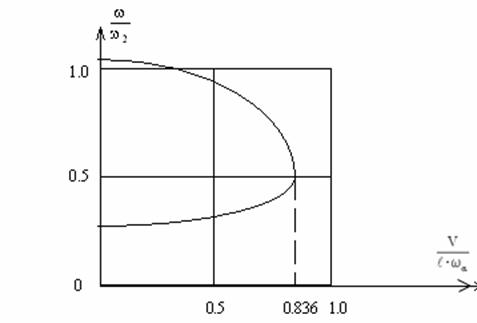
Рис. 66
При V=0 система имеет две частоты собственных колебаний, мало отличающиеся от частот чисто крутильных и чисто изгибных колебаний. С увеличением скорости потока частоты сближаются, и при скорости флаттера оказываются равными друг другу.
Наличие
кратных собственных частот для консервативной системы не связано с какими-либо
особенностями её поведения. Для неконсервативной системы, которую представляет
собой крыло, находящееся в потоке воздуха, слияние двух частот ведёт к потере
устойчивости движения. В процессе колебаний система начинает
интенсивно потреблять энергию потока и амплитуды колебаний неограниченно
возрастают. Механизм этого явления легко понять, если представить себе,
что происходящие с одинаковой частотой крутильные и изгибные колебания крыла
сдвинуты по фазе на 
, так что, когда крыло движется вверх, его угол атаки (а
значит, и подъёмная сила) больше, чем когда оно движется вниз. При этом за
полный цикл подъёмная сила будет совершать положительную работу
и энергия колебания будет непрерывно возрастать.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Строительная механика Теория машин и механизмов
