Главная
5. Расчет и выбор
шпоночных, штифтовых, шлицевых и клиновых соединений
Клиновые соединения
Клиновые соединения используются там, где удобство и
быстрота сборки и разборки имеют решающее значение, например, в зажимных
устройствах. В зависимости от метода сборки и характера воспринимаемых нагрузок
различают ненапряженные клиновые соединения (собираемые без предварительной
затяжки) и напряженные (собираемые с предварительной затяжкой).
Расчет на прочность клиновых соединений любого типа
выполняют по единой методике, однако в качестве расчетной нагрузки для
напряженного клинового соединения принимается нагрузка на 25% выше наибольшей
внешней нагрузки:
Р0 = 1,25P,
где
Р – наибольшая внешняя нагрузка.
Самотормозящиеся клинья выполняют с уклоном 1:100;
1:30; 1:20, a клинья установочные – с уклоном
1:10; 1:6; 1:4.
Расчет
напряженного клинового соединения выполняют в следующей последовательности.
Толщину клина δ (рис. 1) назначают с
таким расчетом, чтобы обеспечить равнопрочность
стержня на разрыв и смятие под клином. Этому требованию удовлетворяет значение
𝛿 = (0,25…0,35)d.
Если
принять δ = 0,25d, то
диаметр хвостовика стержня d можно
определить расчётом на растяжение по формуле
где [σ]P – допускаемое напряжение при растяжении. Для стержней
из сталей марок Ст.4, Ст.5, 35 и 45, работающих при
знакопеременных нагрузках, принимают равным [σ]P = 60...90 МПа.
Рис.1. Схема
к расчету клинового соединения
Во
избежание смятия опорной поверхности втулки
её диаметр в верхней части D принимают равным:
для
чугунной втулки D = 2d,
для
стального литья D = 1,8d.
Диаметр
нижней части втулки D1 принимают равным D1 = (0,8…0,9)D.
Полученный диаметр D1
проверяют расчетом втулки на растяжение по формуле
где [σ]P – допускаемые напряжения на растяжение при
работе с ударами принимают равным: для чугунной втулки [σ]P≤25…30 МПа, для втулки из стального литья
[σ]P≤35…40 МПа.
Расстояние от гнезда клина до торцевой поверхности
хвостовика стержня h1 и расстояние от гнезда клина до торцевой поверхности
втулки h2 принимают равными
h1 = h2 = (0,6...0,8)d
Размеры
h1 и h2проверяют
расчетом хвостовика стержня и втулки на срез по формулам:
для стержня
для втулки
где [τ]С
– допускаемые напряжения на срез при работе соединения с, ударами принимают
равным для чугунной втулки [τ]С = 20...25 МПа и для втулки из стального литья [τ]С = 20…35 МПа.
Диаметр бурта стержня d1
определяют из расчета нижнего основания бурта на смятие по формуле
где [σ]см – допускаемые напряжения смятия; для
стального стержня и чугунной втулки принимают [σ]см = 50...60 МПа;
для стального стержня и втулки из стального литья [σ]см = 80...90 МПа.
Толщину
бурта ∆ можно определить расчетом бурта на изгиб по формуле
где [σ]и
– допускаемое напряжение на изгиб для бурта стального стержня, [σ]и = 60...90 МПа.
При определении диаметра хвостовика стержня d толщина клина δ
принималась равной δ = 0,25d
Высоту клина h (рис. 1) определяют из расчета клина на изгиб по
формуле
где М – момент, изгибающий клин
[σ]И
– допускаемые напряжения на изгиб. Для клина из сталей марок Ст.4, Ст.5, 40 и
45 эти напряжения принимают повышенными [σ]И = 100..150 МПа.
Опорные
поверхности клина со стержнем и втулкой проверяют на смятие по формулам:
для клина и стержня
для клина и втулки
где [σ]см – допускаемые напряжения смятия
принимают равными для стального клина и стержня [σ]см = 150...200 МПа; для стального стержня и
чугунной втулки [σ]см = 80...120 МПа.
а для стального стержня и втулки из стального литья [σ]см = 120...150 МПа.
Длину
клина L принимают равной
L = (1,2…1,5)D.
Пример 1
Рассчитать напряженное клиновое соединение. Сила, действующая на
стержень, 600 кН. Материал клина и стержня –
сталь, втулки – чугунное литье.
Решение.
Определяем диаметр хвостовика стержня из расчета на растяжение его
сечения с отверстием для клина
По
ГОСТ 6636-60 принимаем d = 160 мм.
Толщина
клина равна δ = 0,25·d = 0,25·160 = 40 мм.
Диаметр
верхней части D чугунной втулки по условию
смятия её опорной поверхности
принимаем D = 2d = 2·160 = 320 мм.
Диаметр
нижней части втулки D1 принимаем
D1 = (0,8...0,9)D = (0,8...0.9)∙320 = 280 мм.
Проверяем
полученный диаметр D1 расчетом втулки на растяжение
что меньше допускаемого для чугунной втулки напряжения
[σ]см = 25...30 МПа. Следовательно, диаметр втулки D1 = 280
мм рассчитан правильно.
Расстояния
h1 и h2
принимаем равными
h1 = h2 = (0,6...0,8)∙ d = (0,6...0,8)·160 = 110 мм.
Проверяем
полученные величины h1 и h2 расчетом хвостовика стержня на срез:
для
стержня
что
соответствует допускаемому для стали напряжению [τ]С = 20...35 МПа;
для
втулки
что
соответствует допускаемому для чугунной втулки напряжению [τ]С = 20...25 МПа.
Определяем диаметр бурта стержня d1 из расчета его на смятие:
По
ГОСТ 6636-69 принимаем d1 = 210 мм.
Толщину бурта ∆ стержня определяем из расчета
бурта на изгиб.
Принимаем
∆ = 40 мм.
Высоту
клина h, определяем из его расчета
на изгиб под действием момента:
По
ГОСТ 6630-69 принимаем h = 180 мм .
Проверяем
на смятие опорные поверхности:
клина
и стержня
𝜎СМ = 1,25 – P/(𝛿·d) = 1,25·600·103/(40·160) = 117 МПа,
что
меньше допускаемого [σ]СМ = 150... 200 Мпа
– σСМ<[σ]СМ;
клина
и втулки
что
также меньше допускаемого напряжения для чугунной втулки [σ]СМ = 80...120 Мпа
– σСМ<[σ]СМ.
Длину
клина принимаем равной
L = (1,2…1,5)D1 = 450 мм.
Соединения штифтами
Штифты применяют в качестве установочных элементов для
фиксации взаимного положения деталей (например, крышки и картера редуктора). В
некоторых случаях, штифты используют в соединениях, воспринимающих сдвигающие
нагрузки (например, фланцевые соединения, соединения деталей с валом). Иногда
штифты применяют в качестве элемента, предохраняющего конструкцию от
перегрузки.
Гладкие цилиндрические штифты (ГОСТ 3128-70) обычно
устанавливают в отверстие с натягом 
. При этом
штифт удерживается от выпадения силами трения. Если цилиндрический штифт не
передает нагрузки, а используется для центрирования деталей, то его насаживают
в одну деталь с натягом, а в другую – с зазором (F9, D11). При
разборке штифт остается в одной из деталей и, его посадка не нарушается.
Большее распространение получили гладкие и
конические штифты (ГОСТ 3129-70), которые выполняют с конусностью 1:50. По сравнению с цилиндрическими они обладают тем преимуществом, что
могут быть поставлены в одно и то же отверстие неоднократно.
Диаметр штифта рассчитывают из условия его работы на
срез. В случае нагружения соединения поперечной силой
Р (рис. 2) условие прочности будет.
Рис.2.
Расчетные схемы штифтовых соединений при нагружении
крутящим моментом (а) или сдвигающей
силой (б)
Отсюда
где
z –
число штифтов в соединение
В
случае нагружения соединения крутящим моментом
(рис. 2, а):
Для
конических штифтов d – средний диаметр.
Материал штифтов – преимущественно сталь 45 с НRС 35...42. В качестве [τ]СР
рекомендуется значение [τ]СР = 80 МПа.
Пример 2
Рассчитать цилиндрический штифт крепления шестерни на
валу (рис. 2). Диаметр вала dв = 60 мм; крутящий момент МК = 200 Нм.
Решение.
Принимая рекомендуемое для штифтов значение
допускаемых напряжений среза [τ]СР = 60 МПа, вычисляем диаметр штифта:
По
ГОСТ 3128-70 принимаем диаметр штифта 10 мм.
Для передачи заданного момента кручения в соединении необходимо
применить стандартный цилиндрический штифт.
Штифт 10h11×85 ГОСТ 3128-70.
Вильчатый кривошип укреплен на валу с помощью
цилиндрического штифта (рис. 3) и нагружен силой F = 2,5 кН. Проверить прочность штифтового соединения на срез и
смятие, если 
и 
.
Рис.3
Решение.
Сначала следует определить величину силы F1,
передаваемую на штифт от силы F, приложенной к кривошипу. Очевидно, что М=F·h равен моменту 
. Следовательно,
Проверим прочность штифта на срез под действием силы F1. В
продольном сечении штифта возникает касательное напряжение среза, величина
которого определяется по формуле
, где Аср=d∙ℓ.
Таким
образом
Цилиндрическая поверхность штифта под действием силы F1
подвергается смятию. Поверхность контакта, через которую передается сила F1,
представляет собой четвертую часть поверхности полуцилиндра, так как за уловную
площадь смятия принимается площадь проекции поверхности контакта на
диаметральную плоскость, т.е. dℓ, то Асм = 0,5dℓ.
Тогда
Итак, прочность штифтового соединения обеспечена.
Шпонки применяют преимущественно для передачи
крутящего момента от вала к ступице, насажанной на вал детали и наоборот. Шпоночные
соединения различают на ненапряженные, осуществляемые
призматическими или сегментными шпонками, и напряженные, осуществляемые
клиновыми и тангенциальными шпонками.
Призматические шпонки (рис. 4) выполняют прямоугольного сечения (ГОСТ
23360-78 или СТ СЭВ 189-75). Рабочими у них являются
ботовые, более узкие грани. Шпонка удерживается в пазу вала силами трения за
счет посадки с натягом 
. Ширину шпонок выбирают равной b = (0,25...6,3)d. Длину шпонки ℓ принимают в соответствии
с длиной ступицы колеса или по расчету из условия прочности на смятие. Принятое
значение длины шпонки должно быть согласовано с СТ СЭВ
189-75 ( 14, 16, 18, 20, 22, 25, 28, 36. 40, 45, 50,56, 63, 70, 80, 90, 100,
110. 125, 140, 160, 180, 200).
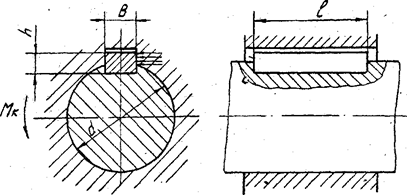
Рис.4. Схема
расчета призматической шпонки
Условие
прочности призматической шпонки на срез имеет вид
МК ≤ 0,5·d·b·ℓ·[τ]СР
где
d – номинальный
диаметр вала;
b – ширина
шпонки;
ℓ
– длина шпонки;
[τ]СР – допускаемое напряжение среза для
стальных шпонок принимают равным [τ]СР = 60...90 МПа.
Поскольку размеры сечений шпонок стандартизованы и
принимаются в зависимости от диаметра вала d, то их расчет сводится к проверке выбранных размеров
по напряжениям смятия:
где h – высота шпонки.
[σ]СМ
– допускаемое напряжение смятия, для стальной шпонки и чугунной ступицы [σ]СМ = 60...80 МПа; для стальных шпонки и ступицы [σ]СМ = 120...150 МПа.
Пример 4
Подобрать стандартную призматическую шпонку и
проверить её на прочность. Диаметр
вала d = 30 мм;
момент, передаваемый валом, МК = 240 Нм. Ступица детали
насаженной на вал, стальная. Допускаемые напряжения при стальных шпонке и
ступице [σ]СМ = 120 МПа.
Решение.
По ГОСТ 23360-78 или СТ СЭВ
189-75 в соответствии с заданным диаметром вала d = 30 мм
выбираем призматическую шпонку с размерами b = 8 мм; h = 7 мм.
Длину
шпонки определяем из условия отсутствия смятия боковых поверхностей в
соединении по формуле
где
[σ]СМ = 120 МПа.
По
СТ СЭВ 189-75 принимаем стандартную длину шпонки ℓ = 40 мм.
Определяем
напряжения среза в шпонке
что
меньше допускаемого напряжения [τ]СР = 60...80 МПа.
Условное
обозначение принятой шпонки:
Шпонка 8×7×40 ГОСТ
23360-78.
Сегментные шпонки (ГОСТ 24071-80 или СТ СЭВ
647-77) не требуют ручной пригонки при монтаже (рис.5) и обладают устойчивым
положением в пазу вала.
Сегментные
шпонки рассчитывают на срез по той же формуле, что и призматические шпонки.
Стандартные сегментные шпонки проверяют на смятие по формуле
где
m – часть высоты шпонки, помещённая в ступицу колеса (рис. 5).
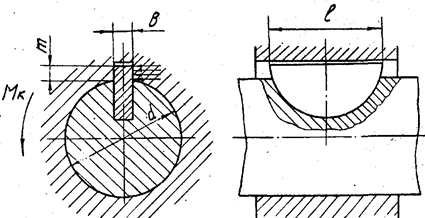
Рис.5. Схема
к расчету сегментной шпонки
Пример 5
Подобрать по стандарту сегментную шпонку. Диаметр вала
d = 40 мм.
Момент, передаваемый соединением, МК = 190 Нм. Ступица стальная.
Решение.
По ГОСТ 24071-80 для вала d = 40 мм
предусмотрена сегментная шпонка с размерами b = 12 мм; h = 19 мм.
Определяем
напряжения смятия
σСМ < [σ]СМ меньше допускаемого для стальной ступицы [σ]СМ = 120…150 МПа.
Условное
обозначение принятой шпонки:
Шпонка 12×19×40 ГОСТ
24071-80.
Клиновые шпонки (ГОСТ 24068-80 или СТ СЭВ 645-77)
представляют собой односкосные клинья о уклоном 1:100
(рис.6).
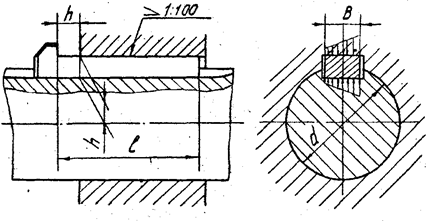
Рис.6. Схема
к расчету клиновой шпонки
В отличие от призматических шпонок у клиновых шпонок рабочими являются
не боковые, а широкие грани, прилегающие к валу и ступице в радиальном
направлении. Клиновые шпонки создают напряженные соединения, способные
передавать не только крутящий момент, но и осевое усилие. Достоинством
соединений клиновыми шпонками является отсутствие зазоров и поэтому хорошее
восприятие ударных нагрузок. Однако в точном машиностроении они совершенно не
используются из-за радиального смещения осей вала и ступицы.
Клиновые
шпонки рассчитывают из условия прочности на смятие
где
f – коэффициент
трения между валом, ступицей и шпонкой, f = 0,13...0,18.
Пример 6
Подобрать
стандартную клиновую шпонку и проверить её
на прочность. Диаметр вала d = 40 мм; крутящий момент, передаваемый
соединением, МК = 600
Нм. Ступица стальная.
Решение.
По
ГОСТ 24068-80 для диаметра вала d = 40 мм предусмотрена клиновая шпонка
сечением b = 12 мм; h = 8 мм.
Из
условия отсутствия смятия определим длину шпонки
По ГОСТ 23360-78 принимаем стандартную длину шпонки ℓ = 125 мм.
Определяем
напряжения смятия в стандартной клиновой шпонке:
что
меньше допускаемого напряжения для стальной ступицы [σ]СМ = 120 МПа.
Условное
обозначение клиновой шпонки.
Шпонка 12×8×125 ГОСТ 24068-80.
Соединения
с тангенциальными клиновыми шпонками (ГОСТ 24069-80 или ОТ СЭВ
646-77) отличаются от соединений простыми клиновыми шпонками тем, что натяг
между валом и ступицей создается не в радиальном, а в касательном направлении,
в связи с чем необходима установка двух шпонок
(рис. 7). В таких соединениях шпонки работают на сжатие, т.е. в лучших
условиях, чем другие типы шпонок.
Рис.7.
Соединение тангенциальными шпонками
Соединения тангенциальными шпонками
в тяжелом машиностроении нашли широкое применение, а также при больших
динамических нагрузках. Расчет таких соединений ведут, исходя из работы только
одной шпонки, так как каждая шпонка передает момент в одну сторону.
Крутящий момент, передаваемый тангенциальной шпонкой
равен
где t – ширина рабочей грани шпонки; С
– ширина фаски рабочей грани шпонки.
Пример 7
Подобрать
стандартные тангенциальные шпонки и проверить их на прочность. Диаметр вала d = 80 мм,
крутящий момент МК = 2
кНм. Ступица стальная.
Решение.
По
ГОСТ 24069-80 для диаметра вала d = 80 мм тангенциальные нормальные
шпонки имеют размеры; b = 24 мм; t = 8 мм; фаска С = 1,5 мм.
Из условия прочности шпонок на смятие определяем их длину
ℓ
По
ГОСТ 23360-78 принимаем стандартную длину шпонки ℓ = 80 мм.
Проверяем
соединение тангенциальными шпонками по напряжениям смятия:
что
меньше допускаемого напряжения на смятие для стальной ступицы [σ]СМ = 120…150 МПа.
Условное обозначение тангенциальной нормальной
шпонки:
Шпонка 8×24×80 ГОСТ 24069-80.
Пример 8
Подобрать призматическую шпонку для соединения стального
зубчатого колеса с валом диаметром d
=
Решение.
Согласно стандарту (см. табл.1), на призматические
шпонки по заданному диаметру вала берем шпонку с размерами: b =
Таблица 1. ГОСТ 23360 – 78
|
|
||||
|
Диаметр вала d |
Сечение шпонки b×h |
Глубина паза |
Фаска s x 450 |
|
|
вала t1 |
втулки t2 |
|||
|
Св. 10 до 12 |
4×4 |
2,5 |
1,8 |
0,08 – 0,16 |
|
от 12 до 17 |
5×5 |
3,0 |
2,3 |
0,16 – 0,25 |
|
от 17 до 22 |
6×6 |
3,5 |
2,8 |
|
|
от 22 до 30 |
8×7 |
4,0 |
3,3 |
|
|
от 30 до 38 |
10×8 |
5,0 |
3,3 |
0,25 – 0,40 |
|
от 38 до 44 |
12×8 |
5,0 |
3,3 |
|
|
от 44 до 50 |
14×9 |
5,5 |
3,8 |
|
|
от 50 до 58 |
16×10 |
6,0 |
4,3 |
|
|
от 58 до 65 |
18×11 |
7,0 |
4,4 |
|
|
от 65 до 75 |
20×12 |
7,5 |
4,9 |
0,40 – 0,60 |
|
от 75 до 85 |
22×14 |
9,0 |
5,4 |
|
|
от 85 до 95 |
25×14 |
9,0 |
5,4 |
|
|
от 95 до 110 |
28×16 |
10,0 |
6,4 |
|
|
Примечания: 1.
Длину шпонки выбирают из ряда: 6; 8; 10; 12; 14; 16; 18; 20; 25; 28; 32; 36; 40;
45; 50; 56; 63; 70; 80; 90; 100; 110; 125; 140; 160; 180; 200 … (до 500). 2.
Материал шпонок – сталь чистотянутая с временным сопротивлением
разрыву не менее 590 МПа. |
||||
Допускаемые напряжения на смятие для неподвижных
шпоночных соединений принимаются в зависимости от предела текучести:
где [S] – допускаемый
коэффициент запаса прочности [S] = 1,9...2,3
при постоянной нереверсивной нагрузке; [S] = 2,9...3,5 при переменной нереверсивной нагрузке;
при реверсивной нагрузке значения [S]
увеличиваются на 30%. При чугунных ступицах [σCM] = 70...100 МПа. Для подвижных шпоночных соединений в
целях предупреждения задира и ограничения износа допускаемые напряжения смятия
уменьшают в 3 – 4 раза.
Допускаемые напряжения на срез для шпонок принимают в
пределах
[τCP] =60…100 МПа
(меньшие значения берут при динамических нагрузках).
Принимая материал шпонки сталь 45 с пределом текучести
σT= 350 МПа, а допускаемый коэффициент запаса прочности
[S] = 2,5 (нагрузка постоянная реверсивная), определим
допускаемое напряжение
Проверяем соединение на смятие:
Проверяем соединение на срез:
29
МПа < 60 МПа
прочность на срез обеспечена.
Пример 9
Зубчатое колесо А
соединено с валом В призматической
шпонкой (рис. 8). С зубчатого колеса передается на вал диаметром d =40 мм момент М = 200 Нм.
Определить длину ℓ
призматической шпонки, учитывая, что допускаемые напряжения материала шпонки
равны: на срез [τCP] =80
МПа, а на смятие [σCM] =140
МПа (размеры на рис. указаны в мм).
Решение.
Определяем усилие F, действующее на шпонку со стороны соединяемых
деталей. Момент, передаваемый на вал равен 
, где d – диаметр вала. Откуда
Предполагается,
что усилие F равномерно
распределено по площади шпонки 
, где ℓ
- длина шпонки, h – ее высота.
Длина шпонки, необходимая для обеспечения ее
прочности, может быть найдена из условия прочности на срез
(1)
Рис.8
и условия прочности на смятие
(2)
Находим длину шпонки из условия прочности на срез, так
как срез происходит по площади Аср = в·ℓ,
то 
или
Из условия прочности (2) на смятие, имеем:
Для обеспечения прочности соединения длину шпонки
необходимо принять равной большему значению из двух полученных, т.е. ℓ=18 мм.
Шлицевые
соединения
Шлицевые
соединения представляют собой многошпоночные соединения, у которых шпонки
выполнены за одно целое с валом (рис. 9).
Рис. 9.
Схема к расчету шлицевого соединения
К
достоинствам шлицевых соединений относят большую несущую способность и большую
усталостную прочность вала, лучшее центрирование втулки на валу. По
геометрической форме шлицев различают прямобочные, эвольвентные и треугольные шлицевые соединения.
Расчет шлицевых соединений производят на смятие по
формуле
где z – число шлицев (зубьев);
ℓ
– длина поверхности контакта зубьев,
равная длине ступицы;
h – высота
поверхности контакта зубьев;
dСР – средний
диаметр поверхности контакта зубьев;
𝜓 – коэффициент,
учитывающий неравномерность распределения нагрузки по зубьям, ψ= 0,75;
[σ]СМ
– допускаемое напряжение смятия для шлицевых соединений, принимается по
табл. 2.
Таблица 2. Допускаемые напряжения смятия для шлицевых
соединений, МПа.
|
Вид соединения |
Условия |
Поверхность шлицев |
|
|
Без термообраб. |
с термообраб. |
||
|
Неподвижное |
а |
35…50 |
40…70 |
|
б |
60…100 |
100…140 |
|
|
в |
80…120 |
120…200 |
|
|
Подвижное не под нагрузкой |
а |
15…20 |
20…35 |
|
б |
20…30 |
30…60 |
|
|
в |
25…40 |
40…70 |
|
|
Подвижное под нагрузкой |
а |
– |
3…10 |
|
б |
– |
5…15 |
|
|
в |
– |
10…20 |
|
|
Примечание:
а – тяжелые (знакопеременная с ударами в
обоих направлениях), б –
средние (слабые толчки), в – легкие (нагрузка спокойная) |
|||
Для
прямобочного профиля (ГОСТ 1139-80 или ОТ СЭВ 188-75) высота поверхности контакта зубьев равна:
средний
диаметр поверхности контакта зубьев:
Для
эвольвентного профиля (ГОСТ 6033-80 или СТ СЭВ
269-76) высота поверхности контакта зубьев равна:
h = m = de/z;
средний
диаметр поверхности контакта зубьев:
dСР = de = m·z,
где m – модуль зацепления зубьев.
Пример 10
Подобрать стандартное неподвижное шлицевое соединение
шестерни с валом и проверить его на прочность. Диаметр вала d = 60 мм;
передаваемый крутящий момент МК = 80 Нм. Нагрузка со слабыми
толчками. Шлицы без термообработки.
Решение.
Принимаем
по ГОСТ 1139-70 прямобочное шлицевое соединение D – 8×52×60×10 .
Длину ступицы шестерни определяем из
условия отсутствия смятия боковой поверхности шлицев:
где
Полученную длину ступицы шестерни
округляем, в соответствии с ГОСТ 6636-69, до величины ℓ = 28 мм.
Проверяем напряжения смятия в шлицевом
соединении;
Это напряжение меньше
допускаемого для неподвижного шлицевого соединения при нагрузке со слабыми
толчками и шлицах без термообработки [σ]СМ = 60...100 МПа.
Обозначение прямобочного
шлицевого соединения при центрировании по наружному диаметру 60 
:
ГОСТ 1139 – 80.
Пример 11
Подобрать шлицевое неподвижное соединение
зубчатого колеса с валом. Соединение передает момент T=189,5 Нм при спокойной нагрузке. Диаметр вала d=45 мм, материал - сталь 45 с
термообработкой - улучшение 290 НВ.
Решение.
Выбор соединения.
Принимаем прямобочное соединение как наиболее распространенное
с центрированием по наружному диаметру.
Размеры
соединения. Для
диаметра вала d = 45 мм.
мм;
SF=600 мм2.
Допускаемые напряжения. Для улучшенной стали при спокойной
нагрузке [σCM] = 60 Н/мм2;
[σ]изн= 0,032НВ= 0,032∙290=9,3 Н/мм2.
Расчетная длина
зубьев. Так как [σ]см>[σ]изн, расчет ведем по формуле:
Длина
ступицы колеса
- согласуется со стандартом.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Строительная механика Теория машин и механизмов
