Главная

Поверхности и объемы тел

8. Вычисление поверхностей и объемов тел

Фигура*	Поверхность F. Боковая поверхность Fб	Расстояние до центра тяжести x0, у0	Объем V
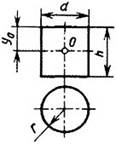
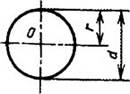
Цилиндр	F = 2πr(r + h) = (1/2) πd (d+2h); Fб = 2πrh= πdh	y0 = h/2	V = πr^2h = (πd^2/4) h
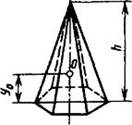
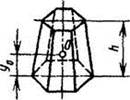
Пирамида	F= сумме площадей треугольников + площадь основания	y0 = (1/4) h	V= площадь основания × h/3
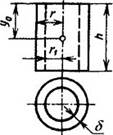
Полый цилиндр (труба)	Fб = внутренняя + внешняя поверхность	y0 = h/2	V = πh(r^2 – r1^2) = πhδ(r + r1)
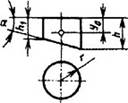
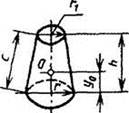
Косорезаный цилиндр	Fб = πr(h + h1)	y0 = (h+h1)/4 + (1/4)((r^2tg^2α)/(h+h1))	V = πr^2 · (h+h1)/2
Шар	F = 4πr^2 = πd^2	–	V = (4/3)πr^3 = πd^3/6 = 0,5236d^3
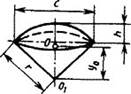
Шаровой сектор	F = (πr/2)(4h + c)	y0 = (3/4)(r – h/2)	V = (2/3)πr^2h
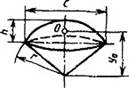
Шаровой сегмент	Fб = 2πrh = (π/4)(c^2 + 4h^2)	y0 = (3/4) ((2r - h)^2 / (3r - h))	V = πh^2(r – h/3) = πh(c2/8 + h2/6)
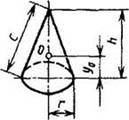
Конус	Fб = πrc = πr	y0 = (1/4)h	V = (1/3)πr^2h
Усеченная пирамида	F= сумме площадей трапеций верхнего и нижнего оснований	y0 = (h/4) · (f2+2+3f1) / (f2++f1)	V = (h/3)(f2 + f1) + (f1, f2 - площади верхнего и нижнего оснований)
Усеченный конус	Fб = πc(r + r1)	y0 = (h/4) · ((r^2 + 2r1r + 3r1^2) / (r2 + r1r + r1^2))	V = (r2 + r1^2 + rr1) · (πh/3)
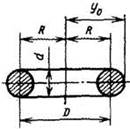
Тор	F = π^2Dd = 9,8996Dd	y0 = R + d/2	V = 2π^2Rr^2 = 19,739Rr^2

*О – центр тяжести

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Строительная механика Теория машин и механизмов

00:00:00